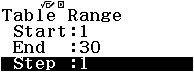
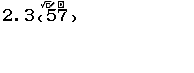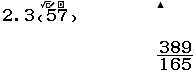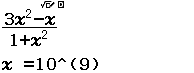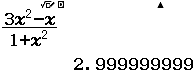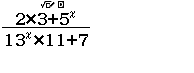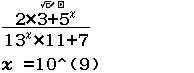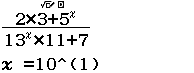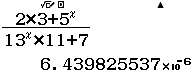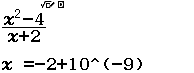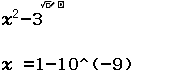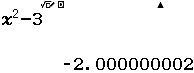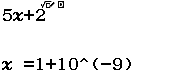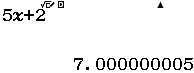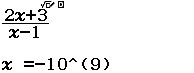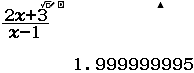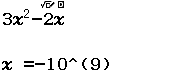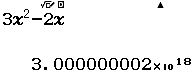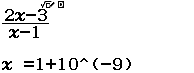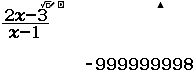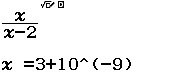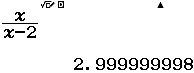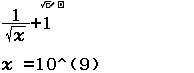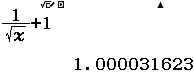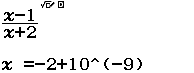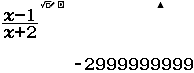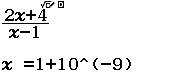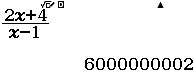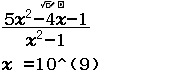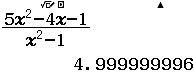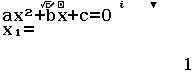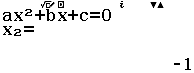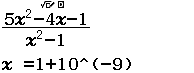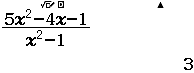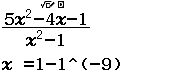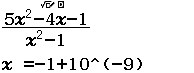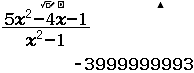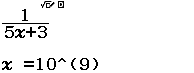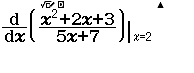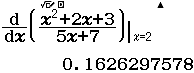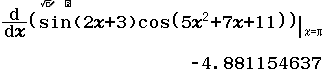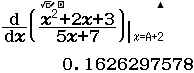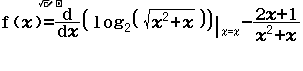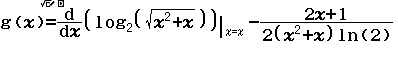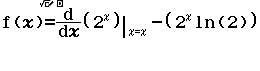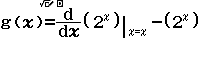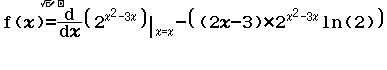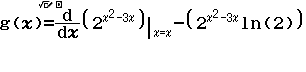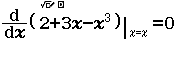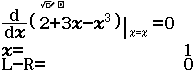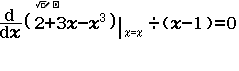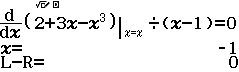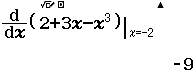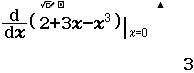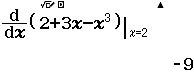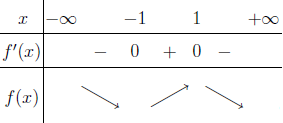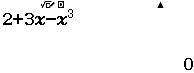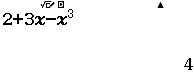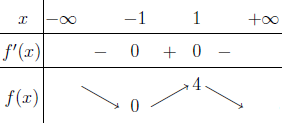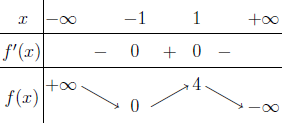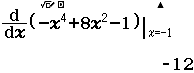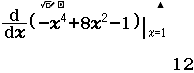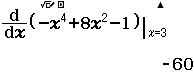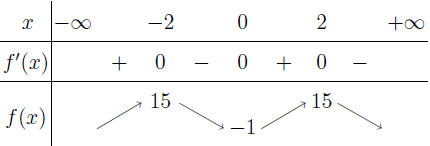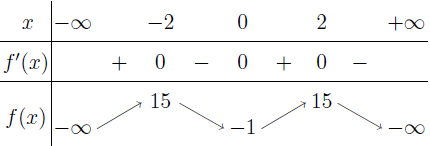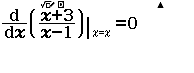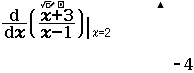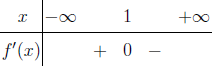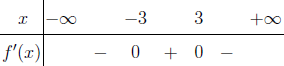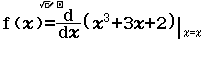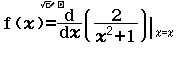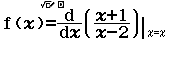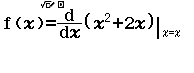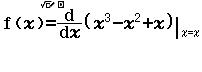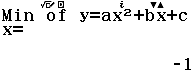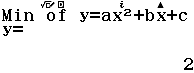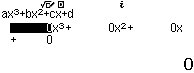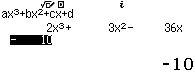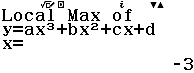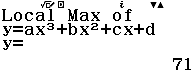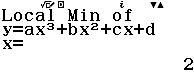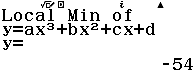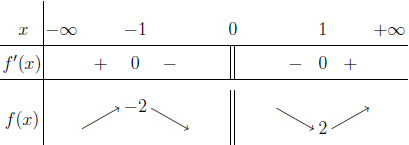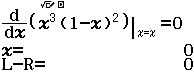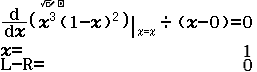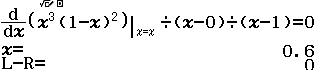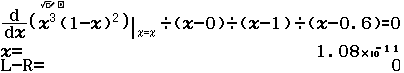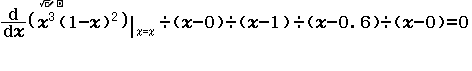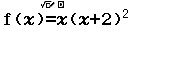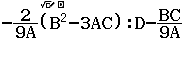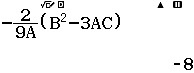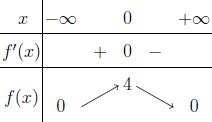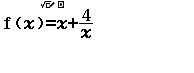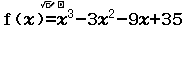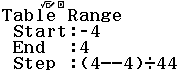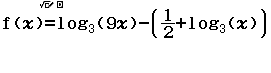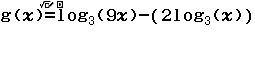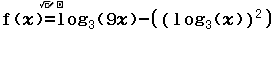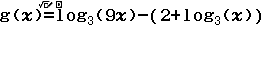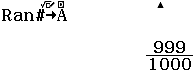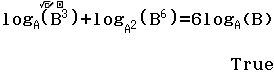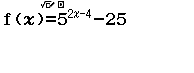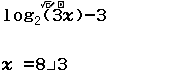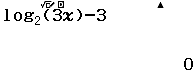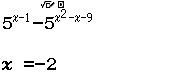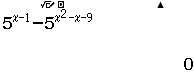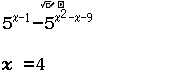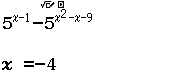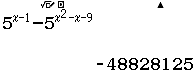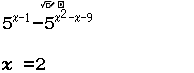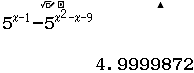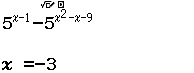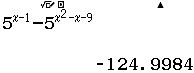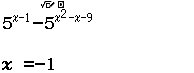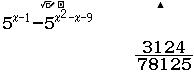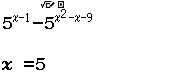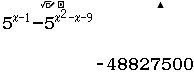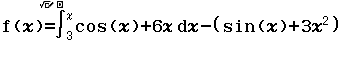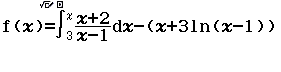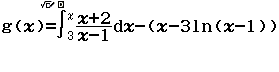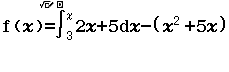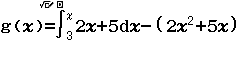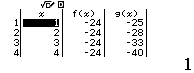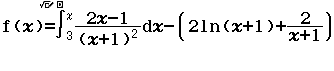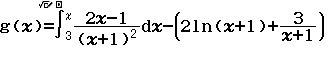Từ năm 2017 Bộ Giáo dục và Đào tạo đã thay đổi hình thức thi của môn Toán từ tự luận sang trắc nghiệm
Với hình thức thi này thì việc sử dụng hiệu quả máy tính Casio fx-580VN X sẽ giúp chúng ta nhanh chóng tìm ra kết quả của bài toán từ đó đạt được kết quả cao trong Kỳ thi
Vậy làm sao để sử dụng hiệu quả?
Câu trả lời mà bạn cần tìm có trong Series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi Trung học Phổ thông Quốc gia
1 Chú ý
Để có để hiểu và vận dụng được các kiến thức trong Series bạn cần có (cả 2)
- Kiến thức cơ bản về Toán học
- Kiến thức cơ bản về máy tính Casio fx-580VN X
Tính $f’’(2)$ biết $f(x)=x^3+2x^2+3x+4$
A. $26$
B. $23$
C. $16$
D. Giá trị khác
Phương pháp 1 Sử dụng kiến thức Toán học
Bước 1 $f’(x)=3x^2+4x+3$
Bước 2 $f’’(x)=6x+4$
Bước 3 $f’’(2)=6.2+4=16$
Phương pháp 2 Sử dụng kiến thức máy tính Casio
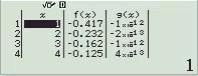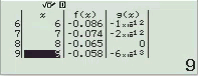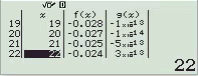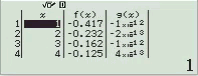
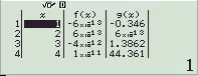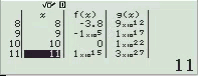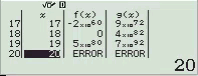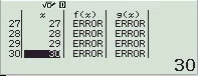
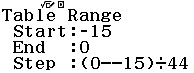
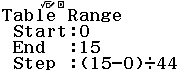
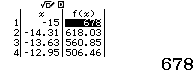
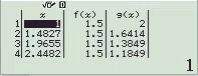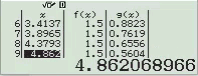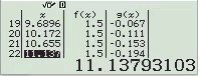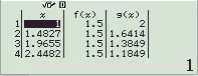
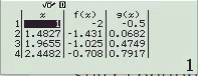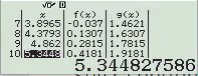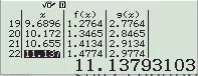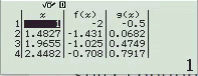
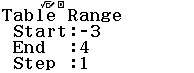
Bước 1 Gán 1 giá trị gần bằng 0 vào biến nhớ A

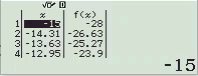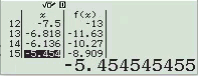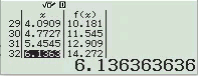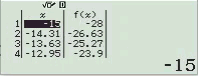
Bước 2 Tính $f’(2)$
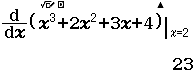
Bước 3 Gán giá trị $f’(2)$ vào biến nhớ B

Bước 4 Tính $f’(2+A)$
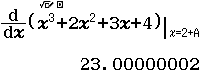
Bước 5 Gán giá trị $f’(2+A)$ vào biến nhớ C
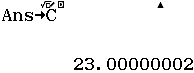
Bước 6 Tính giá trị biểu thức

Dễ thấy việc sử dụng máy tính Casio để tìm ra đáp án của Ví dụ 1.1 là chưa tối ưu
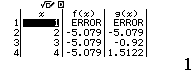
Tính $f’(2)$ biết $f(x)=\dfrac{x^2+2x+3}{\sqrt{x+2}}$
A. $\dfrac{37}{16}$
B. $-\dfrac{37}{16}$
C. $\dfrac{11}{2}$
D. $-\dfrac{11}{2}$
Phương pháp 1 Sử dụng kiến thức Toán học
Bước 1 $f’(x)= \dfrac{x^2+2x+3}{\sqrt{x+2}}=\dfrac{(x^2+2x+3)'(\sqrt{x+2})-(x^2+2x+3)(\sqrt{x+2})’}{(\sqrt{x+2})^2}$
$=\cdots \cdots \cdots$
$=\dfrac{3 x^{2}+10 x+5}{2\sqrt{(x+2)^3}}$
Bước 2 $f’(2)=\dfrac{3 .2^{2}+10 .2+5}{2\sqrt{(2+2)^3}}=\dfrac{37}{16}$
Phương pháp 2 Sử dụng kiến thức máy tính Casio
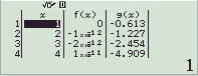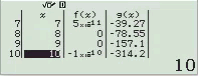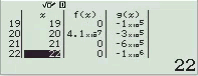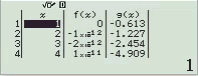
Bước 1 Nhập biểu thức
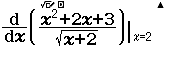
Bước 2 Nhấn phím =
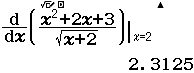
Dễ thấy việc sử dụng máy tính Casio để tìm ra đáp án của Ví dụ 1.2 là phù hợp
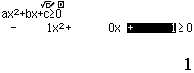
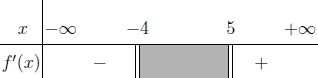
Tập nghiệm của bất phương trình $3^{4-x^2} \geq 27$
A. $[-1, 1]$
B. $(- \infty, 1]$
C. $[\sqrt{7}, \sqrt{7}]$
D. $[1, + \infty)$
Bước 1 Sử dụng kiến thức Toán học
$3^{4-x^2} \geq 27 \Leftrightarrow 3^{4-x^2} \geq 3^3 \Leftrightarrow 3^{4-x^2} – 3^3 \geq 0 \Leftrightarrow 4-x^2-3 \geq 0$
Bước 2 Sử dụng kiến thức máy tính Casio
Đối với bài nếu chỉ sử dụng một mảng kiến thức là Toán học hoặc máy tính Casio vẫn có thể giải được nhưng nếu biết kết hợp cả 2 thì thời gian tìm ra kết quả sẽ nhanh hơn rất nhiều
2 Nội dung chính
- Hàm số lượng giác và phương trình lượng giác
- Tổ hợp và xác suất
- Dãy số, cấp số cộng và cấp số nhân
- Giới hạn
- Đạo hàm
- Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Nguyên hàm, tích phân và ứng dụng
- Số phức
- Phương pháp tọa độ trong không gian
3 Đối tượng hướng đến
- Học sinh Trung học Phổ thông mà đặc biệt là học sinh lớp 12
- Sinh viên chuyên ngành Sư phạm toán học
- Sinh viên đang theo học học phần Toán cao cấp
- Giáo viên giảng dạy bộ môn Toán học
- Những bạn yêu thích tìm hiểu các phương pháp, các thủ thuật máy tính Casio
- …
4 Phương pháp trình bày
- Tập trung khai thác tối đa các tính năng của máy tính
- Tập trung giải thích thuật giải
- Không hướng dẫn chi tiết các tao tác, quy trình bấm máy (chủ yếu hướng dẫn thông qua ảnh chụp màn hình)
- Không chú trọng việc trình bày lời giải
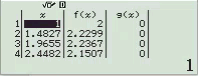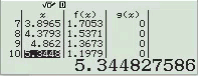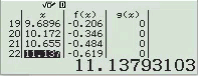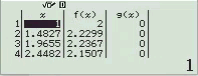
Tìm $\lim \dfrac{3 n^{2}-n}{1+n^{2}}$
Lời giải của sách giáo khoa
Chia tử số và mẫu số cho $n^{2}$ ta được $\dfrac{3 n^{2}-n}{1+n^{2}}=\dfrac{3-\dfrac{1}{n}}{\dfrac{1}{n} \cdot \dfrac{1}{n}+1}$
Vì
- $\lim \left(3-\dfrac{1}{n}\right)=\lim 3-\lim \dfrac{1}{n}=3-0=3$
- $\lim \left(\dfrac{1}{n} \cdot \dfrac{1}{n}+1\right)=\lim \dfrac{1}{n} \cdot \lim \dfrac{1}{n}+\lim 1=0.0+1=1$
Nên $\lim \dfrac{3 n^{2}-n}{1+n^{2}}=\lim \dfrac{3-\dfrac{1}{n}}{\dfrac{1}{n} \cdot \dfrac{1}{n}+1}=\dfrac{\lim \left(3-\dfrac{1}{n}\right)}{\lim \left(\dfrac{1}{n} \cdot \dfrac{1}{n}+1\right)}=\dfrac{3}{1}=3$
“Lời giải” của mình
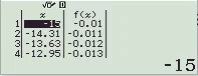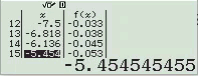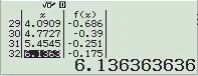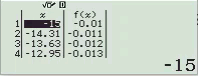
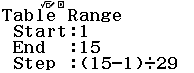
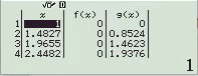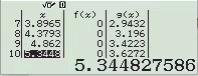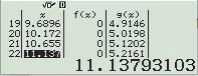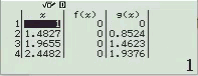
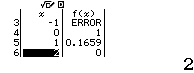
Bước 1 Nhập biểu thức

Bước 2 Nhấn phím CALC => nhập $10^9$ => nhấn phím =
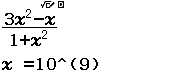
Bước 3 Quan sát kết quả hiển thị trên màn hình ta nhận thấy đây là một số thập phân vô hạn tuần hoàn, cụ thể nó là $2(9)$
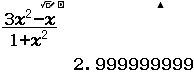
Vậy giới hạn cần tìm là $3$
5 Danh sách bài viết
- Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi Trung học Phổ thông Quốc gia
- Tính giới hạn của dãy số, hàm số
- Tính đạo hàm của hàm số
- Lập bảng biến thiên
- Xét tính đơn điệu
- Tìm cực trị của hàm số
- Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ứng dụng máy tính Casio fx-580VN X giải các dạng toán về hàm số lũy thừa, hàm số mũ và hàm số logarit
- Giải phương trình mũ, phương trình logarit
- Tính nguyên hàm
- Tính tích phân
- Ứng dụng máy tính Casio fx-580VN X giải các dạng toán về số phức
6 Tài liệu tham khảo
- Nguyễn Thái Sơn, Giải nhanh bài thi trắc nghiệm môn toán với sự hỗ trợ của máy tính Casio fx-580VN X, Nhà xuất bản Đại học Sư phạm Thành phố Hồ Chí Minh
- Nguyễn Ngọc Nam, Công phá kỹ thuật Casio, Nhà xuất bản Đại học Quốc gia Hà Nội
- Sách giáo khoa (Đại số & Giải tích 11, Giải tích 12, Hình học 12)
- Series Hướng dẫn sử dụng máy tính Casio fx-580VN X
Mặc dù đã có nhiều cố gắng nhưng không tránh khỏi sai sót. Rất mong nhận được những góp ý quý báu từ các bạn
Bạn có thể góp ý cho mình theo ba cách
- Bình luận trực tiếp bên dưới bài viết
- Liên hệ với mình thông qua form Liên hệ
- Gửi thư điện tử đến địa chỉ [email protected]
Trân trọng cảm ơn