Xét tính đơn điệu của hàm số bằng máy tính Casio fx-580VN X

18/06/202103/03/2023Nhut Nguyen Minh

Bài này thuộc phần 5 trong 12 phần của series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi THPT Quốc gia

Xét tính đơn điệu của hàm số chính xác là xét tính đồng biến, nghịch biến của hàm số trên tập xác định của nó

Hiện tại đã có khá nhiều thủ thuật máy tính Casio fx-580VN giúp chúng ta xét tính đơn điệu của hàm số. Mỗi thủ thuật đều có những ưu điểm và nhược điểm riêng

Nhằm đóng góp vào kho tàng kiến thức của nhân loại 😊. Hôm nay mình sẽ hướng dẫn các bạn hai thủ thuật mới một áp dụng cho bài kiểm tra/ thi tự luận, một áp dụng cho bài kiểm tra/ thi trắc nghiệm

Mục lục nội dung

1 Áp dụng cho bài kiểm tra/ thi tự luận

1.1 Thuật giải

Bước 1 Tìm những điểm làm cho $f'(x)$ không xác định

Bước 2 Tìm những điểm làm cho $f'(x)=0$

Bước 3 Lập Bảng 1 và điền những điểm tìm được ở Bước 1 và Bước 2 vào (sắp xếp theo thứ tự tăng dần)

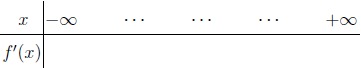
Bước 4 Xác định dấu của $f'(x)$ trên những khoảng tìm được

1.2 Ví dụ

Vì Thuật giải 1.1 chính là phần đầu của Thuật giải 1 nên mình chỉ giới thiệu đáp án chứ không hướng dẫn chi tiết

Chi tiết bạn có thể xem trong bài viết Lập bảng biến thiên bằng máy tính Casio fx-580VN X

Ví dụ 1.2.1

Xét sự đồng biến nghịch biến của hàm số $f(x)=4+2x-x^2$

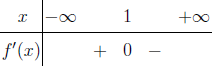
Vậy hàm số đã cho đồng biến trên khoảng $(- \infty; 1)$ , nghịch biến trên khoảng $(1; +\infty)$

Ví dụ 1.2.2

Xét sự đồng biến nghịch biến của hàm số $f(x)=\sqrt{x^2-x-20}$

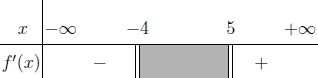
Vậy hàm số đã cho nghịch biến trên khoảng $(- \infty; -4)$ , đồng biến trên khoảng $(5; +\infty)$

Ví dụ 1.2.3

Xét sự đồng biến nghịch biến của hàm số $f(x)=\dfrac{2x}{x^2+9}$

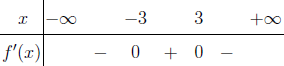
Vậy hàm số đã cho nghịch biến trên các khoảng $(- \infty; -3)$ và $(3; +\infty)$ , đồng biến trên khoảng $(-3; 3)$

2 Áp dụng cho bài kiểm tra/ thi trắc nghiệm

Giải sử chúng ta cần xét tính đồng biến/ nghịch biến của hàm số f(x) với bốn phương án A, B, C và D cho trước

Bước 1 Thiết lập chỉ sử dụng duy nhất hàm f(x)

Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập biểu thức $\dfrac{d}{dx} \left( f(x) \right)|_{x=x}$

Bước 4 Nhập Start = “điểm mút trái”, End = “điểm mút phải”, Step = (“điểm mút phải” – “điểm mút trái”) $\div 44$

Nếu “điểm mút” là $-\infty$ thì nhập $-15$
Nếu “điểm mút” là $+\infty$ thì nhập $+15$

Bước 5 Quan sát bảng giá trị của f(x)

Nếu tất cả các giá trị nhỏ hơn $0$ thì hàm số nghịch biến
Nếu tất cả các giá trị lớn hơn $0$ thì hàm số đồng biến

3 Đôi lời về hai phương pháp này

Phương pháp thứ nhất là phương pháp mình khuyến khích các bạn sử dụng cho cả hai hình thức tự luận và trắc nghiệm
Phương pháp thứ nhì tuy nhiều bước, nhiều thao tác nhưng nếu bạn thực hiện thành thạo thì không tốn bao nhiêu thời gian

4 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia

Giả sử mình đã thiết lập chỉ sử dụng duy nhất hàm f(x) và đã chọn phương thức tính toán Table

Câu 8, Mã đề thi 101, Năm 2017

Cho hàm số $y=x^3+3x+2$ . Mệnh đề nào dưới đây là đúng

A. Hàm số đồng biến trên khoảng $(-\infty; 0)$ và nghịch biến trên khoảng $(0; +\infty)$

B. Hàm số nghịch biến trên khoảng $(-\infty; +\infty)$

C. Hàm số đồng biến trên khoảng $(-\infty; +\infty)$

D. Hàm số nghịch biến trên khoảng $(-\infty; 0)$ và đồng biến trên khoảng $(0; +\infty)$

Bước 1 Kiểm tra phương án A với khoảng $(-\infty; 0)$

Bước 1.1 Nhập biểu thức $\dfrac{d}{dx} (x^3+3x+2)|_{x=x}$

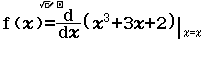
Bước 1.2 Nhập $Start = -15, End = 0, Start = (0--15) \div 44$

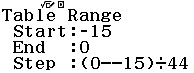
Bước 1.3 Quan sát bảng giá trị của f(x)

Vì tất cả các giá trị tìm được đều dương nên $y$ đồng biến trên khoảng $(-\infty; 0)$

Bước 2 Kiểm tra phương án A với khoảng $(0; +\infty)$

Bước 2.1 Nhập biểu thức $\dfrac{d}{dx} (x^3+3x+2)|_{x=x}$

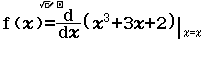
Bước 2.2 Nhập $Start = 0, End = 15, Start = (15-0) \div 44$

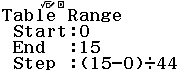
Bước 2.3 Quan sát bảng giá trị của f(x)

Vì các giá trị tìm được dương nên $y$ không nghịch biến trên khoảng $(0; +\infty)$

Suy ra phương án A không là đáp án

Chú ý 4

Trong Toán học để chứng minh là đúng chúng ta cần chứng minh với mọi còn để chứng minh sai chúng ta chỉ cần chỉ ra tồn tại

Bước 3 Kiểm tra phương án B

Bước 3.1 Nhập biểu thức $\dfrac{d}{dx} (x^3+3x+2)|_{x=x}$

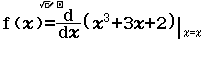
Bước 3.2 Nhập $Start = -15, End = 15, Start = (15--15) \div 44$

Bước 3.3 Quan sát bảng giá trị của f(x)

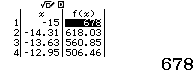
Vì các giá trị tìm được dương nên $y$ không nghịch biến trên khoảng $(-\infty; +\infty)$

Suy ra phương án B không là đáp án

Bước 4 Kiểm tra phương án C

Bước 4.1 Nhập biểu thức $\dfrac{d}{dx} (x^3+3x+2)|_{x=x}$

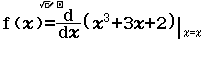
Bước 4.2 Nhập $Start = -15, End = 15, Start = (15--15) \div 44$

Bước 4.3 Quan sát bảng giá trị của f(x)

Vì tất cả các giá trị tìm được đều dương nên $y$ đồng biến trên khoảng $(-\infty; +\infty)$

Suy ra phương án C là đáp án

Câu 13, Mã đề thi 101, Năm 2017

Hàm số $y=\dfrac{2}{x^2+1}$ nghịch biến trên khoảng nào dưới đây

A. $(0; +\infty)$

B. $(-1; 1)$

C. $(-\infty; +\infty)$

D. $(-\infty; 0)$

Bước 1 Kiểm tra phương án A

Bước 1.1 Nhập biểu thức $f(x)=\dfrac{d}{dx} \left( \dfrac{2}{x^2+1} \right)|_{x=x}$

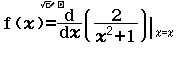
Bước 1.2 Nhập $Start = 0, End = 15, Start = (15-0) \div 44$

Bước 1.3 Quan sát bảng giá trị của f(x)

Vì tất cả các giá trị tìm được đều âm nên $y$ nghịch biến trên khoảng $(0; +\infty)$

Suy ra phương án A là đáp án

Câu 30, Đề thi minh họa, Năm 2021

Hàm số nào dưới đây đồng biến trên R

A. $y=\dfrac{x+1}{x-2}$

B. $y=x^2+2x$

C. $y=x^3-x^2+x$

D. $y=x^4-3x^2+2$

Bước 1 Kiểm tra phương án A

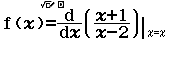
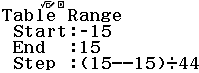
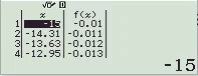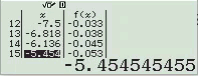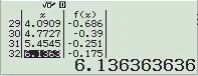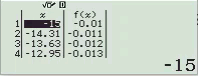
Suy ra $y=\dfrac{x+1}{x-2}$ không đồng biến trên R

Bước 2 Kiểm tra phương án B

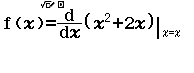
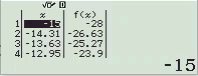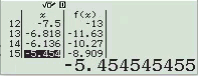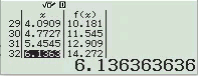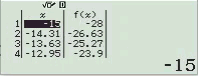
Suy ra $y=x^2+2x$ không đồng biến trên R

Bước 3 Kiểm tra phương án C

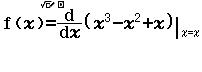
Suy ra $y=x^3-x^2+x$ đồng biến trên R

Bài viết cùng Serie<< Lập bảng biến thiên bằng máy tính Casio fx-580VN XTìm cực trị của hàm số bằng máy tính Casio fx-580VN X >>