Tính nguyên hàm bằng máy tính Casio fx-580VN X
Máy tính Casio fx-580VN X vẫn chưa hỗ trợ chúng ta tính tích phân không xác định tức nguyên hàm một cách trực tiếp. Tuy nhiên nếu biết cách chúng ta vẫn có thể tính được dễ dàng
Cụ thể mình sẽ hướng dẫn các bạn ứng dụng tính năng tích tích phân xác định và phương thức tính toán Table để tìm ra nguyên hàm của một hàm số bất kì dựa trên bốn phương án A, B, C và D

1 Thuật giải
Bước 1 Tìm tập xác định của hàm số
Bước 2 Thiết lập sử dụng cả hàm f(x) và g(x)
Bước 3 Chọn phương thức tính toán Table
Bước 4 Nhập f(x) bằng tích phân của hàm đã cho – hàm ở phương án A
Cận dưới là một giá trị bất kì thuộc tập xác định hoặc khoảng mà đề cho trước, cận trên là ![]()
Bước 5 Tương tự nhập g(x) bằng tích phân của hàm đã cho – hàm ở phương án B
Bước 6 Nhập ![]()
Bước 7 Quan sát bảng giá trị của f(x) và g(x)
- Nếu f(x) là hàm hằng thì phương án A là đáp án
- Nếu g(x) là hàm hằng thì phương án B là đáp án
- Nếu cả f(x) và g(x) đều không là hàm hằng thì kiểm tra với phương án C, D
Họ tất cả các nguyên hàm của hàm số ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã thiết lập sử dụng cả hàm f(x) và g(x), đã chọn phương thức tính toán Table
Dễ thấy tập xác định của hàm số đã cho là ![]()
Bước 1 Nhập f(x) bằng ![]()
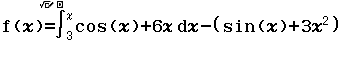
Bước 2 Nhập g(x) bằng ![]()
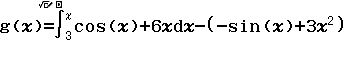
Bước 3 Nhập ![]()
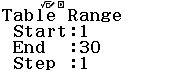
Bước 4 Quan sát bảng giá trị của f(x) và g(x)

Vì tất cả các giá trị của f(x) đều bằng nhau nên f(x) là hàm hằng
Vậy phương án A là đáp án
- Hàm số đã cho có chứa hàm lượng giác nên bạn cần thiết lập đơn vị góc là radian trước khi thực hiện
- Mình chọn cận dưới của tích phân là
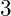 , bạn hoàn toàn có thể chọn một số khác miễn sao thuộc tập xác định
, bạn hoàn toàn có thể chọn một số khác miễn sao thuộc tập xác định
2 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia
Họ tất cả các nguyên hàm của hàm số ![]() trên khoảng
trên khoảng ![]() là
là
A. ![]()
B. ![]()
C. 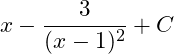
D. 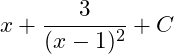
Đề đã cho khoảng tìm nguyên hàm nên chúng ta không cần tìm tập xác định
Bước 1 Nhập hàm f(x)
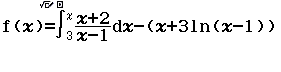
Bước 2 Nhập hàm g(x)
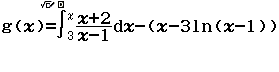
Bước 3 Nhập ![]()

Bước 4 Quan sát bảng giá trị của f(x) và g(x)
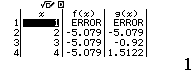
![]() làm máy tính thông báo ERROR nhưng không ảnh hưởng gì đến kết quả. Miễn sau tất cả các giá trị còn lại đều bằng nhau là được
làm máy tính thông báo ERROR nhưng không ảnh hưởng gì đến kết quả. Miễn sau tất cả các giá trị còn lại đều bằng nhau là được
Vậy phương án A là đáp án
Họ tất cả các nguyên hàm của hàm số ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Dễ thấy tập xác định của hàm số đã cho là ![]()
Bước 1 Nhập hàm f(x)
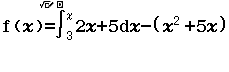
Bước 2 Nhập hàm g(x)
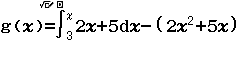
Bước 3 Nhập ![]()
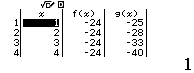
Bước 4 Quan sát bảng giá trị của f(x) và g(x)
Vậy phương án A là đáp án
Họ tất cả các nguyên hàm của hàm số 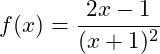 trên khoảng
trên khoảng ![]() là
là
A. 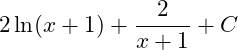
B. 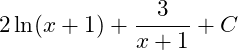
C. 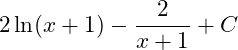
D. 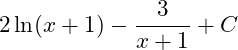
Bước 1 Nhập hàm f(x)
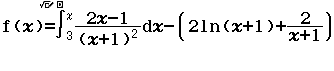
Bước 2 Nhập hàm g(x)
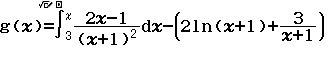
Bước 3 Nhập ![]()

Bước 4 Quan sát bảng giá trị của f(x) và g(x)

Vậy phương án B là đáp án
Thật ra bạn có thể bỏ qua Bước 1 Tìm tập xác định của hàm số. Bạn cứ nhập một số bất kì làm cận dưới (thường chỉ cần chọn số tự nhiên lớn hơn 1 là được)
Trường hợp bạn chọn trúng số làm cho tất cả các giá trị của f(x) thông báo ERROR thì hãy chọn một giá trị khác làm cận dưới
