Giải hệ phương trình, phương trình bằng CASIO fx 580 VN X

Tính năng Equation / Func của máy tính cầm tay CASIO fx 580 VN X cho phép chúng ta giải nhanh hệ phương trình và phương trình

Cụ thể

• Hệ hai phương trình, hệ ba phương trình và hệ bốn phương trình
• Phương trình bậc hai, phương trình bậc ba và phương trình bậc bốn

Ngoài ta tính năng này cũng cho phép chúng ta xác định cực trị của hàm số bậc hai, cực trị hàm số bậc ba

1 Giải hệ phương trình

Chẳng hạn mình cần giải hệ phương trình $\left\{\begin{array}{lll}2x&+y&=4\\-2x&+y&=0\end{array}\right.$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím MENU => nhấn phím 9 để chọn tính năng Equation/Func

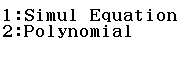
Bước 2 nhấn phím 1 để chọn Simul Equation

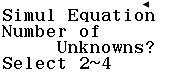
Bước 3 nhấn phím 2 để giải hệ hai phương trình bậc nhất

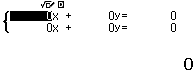
Bước 4 nhấn lần lượt các phím để nhập các hệ số

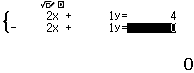
Bước 5 nhấn phím =

Vậy nghiệm của hệ phương trình đã cho là (1, 2)

Một số hệ phương trình khi giải sẽ thu được thông báo

• All Real Numbers tức hệ phương trình đã cho có vô số nghiệm
• No Solution tức hệ phương trình đã cho vô nghiệm

2 Giải phương trình

Chẳng hạng mình cần giải phương trình bậc hai $x^2-3x+2=0$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím MENU => nhấn phím 9 để chọn tính năng Equation / Func

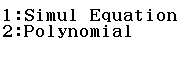
Bước 2 nhấn phím 2 để chọn Polynomial

Bước 3 nhấn phím 2 để khai báo số lượng phương trình của hệ

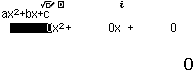
Bước 4 nhấn lần lượt các phím để nhập các hệ số

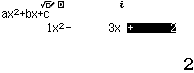
Bước 5 nhấn phím =

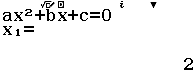
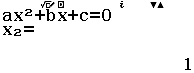
Vậy phương trình đã cho có hai nghiệm là 2, 1

Nếu tiếp tục nhấn phím = chúng ta sẽ tìm được tọa độ điểm cực tiểu của hàm số

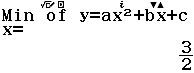
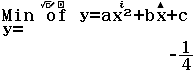
Vậy điểm cực trị (cực tiểu) của hàm số $y=x^2-3x+2$ là $\left(\frac{3}{2}, -\frac{1}{4}\right)$        

3 Lời kết

Trong thực hành không phải bao giờ chúng ta cũng gặp trực tiếp bài toán “giải hệ phương trình …” hoặc “giải phương trình …” để sử dụng ngay tính năng Equation / Func của máy tính cầm tay CASIO fx 580 VN X

Nhiều bài toán khi tiến hành các phép biến đổi sơ cấp sẽ làm xuất hiện hệ phương trình, phương trình tương ứng

Dưới đây là một số bài toán thường gặp …

• Viết phương trình đường thẳng đi qua hai điểm
• Viết phương trình đường cong Parabol đi qua ba điểm
• Viết phương trình đường tròn đi qua ba điểm
• Viết phương trình mặt cầu đi qua bốn điểm
• Viết phương trình đường thẳng đi qua hai điểm cực trị
• Tính khoảng cách giữa hai điểm cực trị

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

Bài viết cùng Serie

<< Sử dụng tính năng Table tạo bảng giá trị trên CASIO fx 580 VN XGiải bất phương trình bằng máy tính cầm tay CASIO fx 580 VN X >>