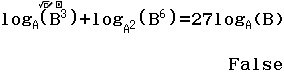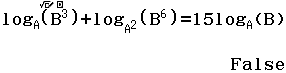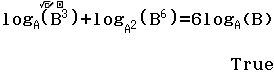Ứng dụng Casio fx-580VN X giải các dạng toán về hàm số lũy thừa/ mũ/ logarit
Chủ điểm về hàm số lũy thừa, hàm số mũ và hàm số logarit có rất nhiều dạng toán khác nhau
Tuy nhiên do thời gian và kiến thức có hạn nên mình chỉ hướng dẫn các bạn hai dạng toán cơ bản nhất cũng là thường gặp nhất trong Kỳ thi Trung học Phổ thông Quốc gia
Tất nhiên mình sẽ hướng dẫn giải bằng máy tính Casio fx-580VN X chứ không bằng kiến thức Toán học. Việc làm này rất có ý nghĩa khi bạn quên các tính chất, định lí về các hàm số trên
1 Trường hợp cho hàm 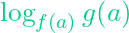
Người ta thường sử dụng biến ![]() cho hàm số logarit nhưng do phương thức tính toán Table chỉ chạy với biến
cho hàm số logarit nhưng do phương thức tính toán Table chỉ chạy với biến ![]() nên chúng ta sẽ thay biến
nên chúng ta sẽ thay biến ![]() bằng biến
bằng biến ![]()
Trước khi thực hiện thuật giải bạn hãy thực hiện
- Thiết lập sử dụng cả hàm f(x) và hàm g(x)
- Chọn phương thức tính toán Table
Bước 1 Nhập f(x) bằng hàm đã cho – hàm ở phương án A
Bước 2 Nhập g(x) bằng hàm đã cho – hàm ở phương án B
Bước 3 Nhập ![]()
Bước 4 Quan sát bảng giá trị của f(x) và g(x)
- Nếu f(x) cho giá trị bằng
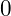 thì phương án A là đáp án
thì phương án A là đáp án - Nếu g(x) cho giá trị bằng
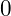 thì phương án B là đáp án
thì phương án B là đáp án - Nếu f(x) và g(x) đều cho giá trị khác
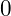 thì kiểm tra với phương án C, D
thì kiểm tra với phương án C, D
Với ![]() là số thực dương tùy ý,
là số thực dương tùy ý, ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Nhập hàm 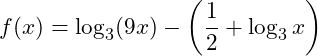
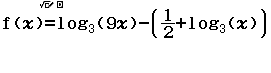
Bước 2 Nhập hàm ![]()
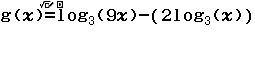
Bước 3 Nhập ![]()
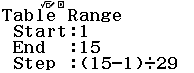
Bước 4 Bảng giá trị của f(x) và g(x)
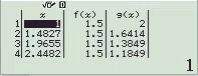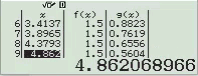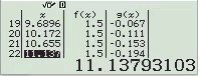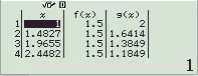
Quan sát bảng trên ta thấy không hàm số nào cho giá trị bằng ![]()
Suy ra phương án A, B không là đáp án
Bước 5 Nhập hàm ![]()
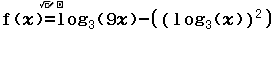
Bước 6 Nhập hàm ![]()
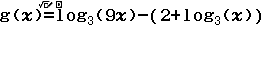
Bước 7 Nhập ![]()

Bước 8 Bảng giá trị của f(x) và g(x)
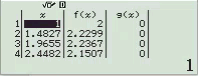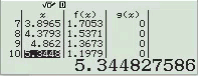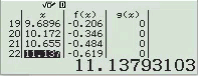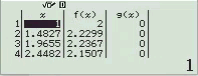
Quan sát bảng giá trị trên thấy hàm số g(x) cho giá trị bằng ![]()
Vậy phương án D là đáp án
2 Trường hợp cho hàm 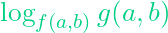
Bước 1 Gán một số bất kì vào biến nhớ A, biến nhớ B
Bước 2 Chọn phương thức tính toán Verify
Bước 3 Nhập hàm đã cho “=” hàm ở phương án A
Bước 4 Nhấn phím =
Quan sát màn hình
- Nếu màn hình hiển thị True thì phương án A là đáp án
- Nếu màn hình hiển thị False thì thực hiện lại Bước 3 với các hàm ở các phương án B, C, D
Với ![]() là các số thực dương tùy ý và
là các số thực dương tùy ý và ![]() khác
khác ![]() , đặt
, đặt ![]() . Mệnh đề nào dưới đây là đúng
. Mệnh đề nào dưới đây là đúng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Gán một số bất kì vào biến nhớ A, biến nhớ B
Bước 2 Chọn phương thức tính toán Verify
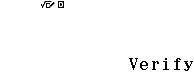
Bước 3 Nhập hàm ![]() “=”
“=” ![]()
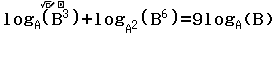
Dấu = ở đây được nhập vào bằng cách nhấn phím OPTN => nhấn phím 1
Bước 4 Nhấn phím =
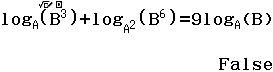
Suy ra phương án A không là đáp án
Bước 5 Kiểm tra với các phương án B, C, D
Vậy phương án D là đáp án
3 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia
Với ![]() là số thực dương tùy ý,
là số thực dương tùy ý, ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Kiểm tra với phương án A, B
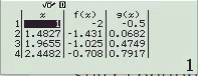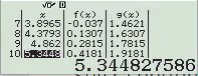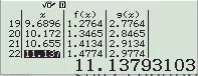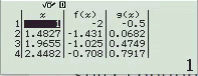
Suy ra phương án A, B không là đáp án
Bước 2 Kiểm tra với phương án C, D
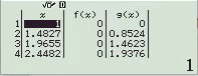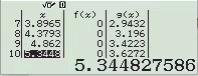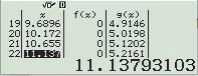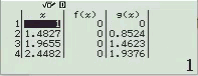
Vậy phương án C là đáp án
Với ![]() là số thực dương tùy ý,
là số thực dương tùy ý, ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Kiểm tra với phương án A, B
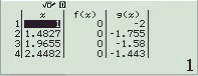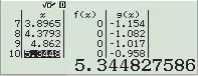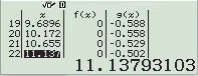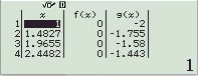
Vậy phương án A là đáp án
Đối với trường hợp cho hàm ![]() thì bạn nên sử dụng phương thức tính toán Table. Biết rằng tính năng CALC, phương thức tính toán Verify vẫn sử dụng được nhưng tốn nhiều thời gian hơn
thì bạn nên sử dụng phương thức tính toán Table. Biết rằng tính năng CALC, phương thức tính toán Verify vẫn sử dụng được nhưng tốn nhiều thời gian hơn
Đối với trường hợp cho hàm ![]() thì bạn có thể dùng tính năng CALC, phương thức tính toán Verify. Trường hợp này không dùng phương thức tính toán Table bởi vì phương thức này hiện chỉ hỗn trợ một biến
thì bạn có thể dùng tính năng CALC, phương thức tính toán Verify. Trường hợp này không dùng phương thức tính toán Table bởi vì phương thức này hiện chỉ hỗn trợ một biến