Tính giới hạn của dãy số, hàm số bằng máy tính Casio fx-580VN X

10/06/202102/05/2022Nhut Nguyen Minh

Bài này thuộc phần 2 trong 12 phần của series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi THPT Quốc gia

Xét tính liên tục của hàm số, tìm đường tiệm cận đứng/ ngang của đồ thị hàm số là các dạng toán thường gặp trong Kỳ thi Trung học Phổ thông Quốc gia

Công việc đầu tiên cần làm để giải quyết được các dạng toán này là tính giới hạn của hàm số tương ứng

Máy tính Casio fx-580VN X có 512 tính năng nhưng không một tính nào cho phép chúng ta tính giới hạn của dãy số/ hàm số

Bài viết này sẽ giới thiệu một thủ thuật giúp bạn tính được giới hạn của dãy số, hàm số bằng máy tính Casio fx-580VN X thông qua tính năng CALC

Mục lục nội dung

1 Giới hạn của dãy số

1.1 Thuật giải

Bước 1 Nhập dãy số vào máy tính, vì máy tính không có biến n nên ta sẽ thay bằng biến x

Bước 2 Nhấn phím CALC => nhập $10^9$ => nhấn phím =

Bước 3 Nếu màn hình hiển thị một số có dạng

Trường hợp 1 $a \times 10^n$ với $(a \in R^+, n \in N^*)$ tức một số vô cùng lớn thì đáp án là $+\infty$
Trường hợp 2 $-a \times 10^n$ với $(a \in R^+, n \in N^*)$ tức một số vô cùng bé thì đáp án là $-\infty$
Trường hợp 3 $a \times 10^{-n}$ với $(a \in R, n \in N^*)$ tức một số gần bằng $0$ thì đáp án là $0$
Trường hợp 4 Thập phân vô hạn tuần hoàn thì đáp án là số thập phân vô hạn tuần hoàn
Trường hợp 5 Thập phân vô hạn không tuần hoàn thì đáp án là số thập phân vô hạn không tuần hoàn

1.2 Chú ý

Một số ít trường hợp khi CALC $10^9$ mà máy báo lỗi Math ERROR thì chúng ta cần giảm số mũ xuống $10^8, 10^7, 10^6, …, 10^1$
Khi màn hình hiển thị kết quả ban đầu làm chúng ta phân vân không biết thuộc Trường hợp 4 hay Trường hợp 5 thì CALC thêm $10^6, 10^{12}$ để có thể phân biệt dễ dàng hơn
Một số cách viết ít gặp trong thực tế nhưng trong Toán học miễn đúng thì vẫn được chấp nhận

Cách viết thường gặp	Cách viết ít gặp
Số $2$ là một số tự nhiên	Số $2$ là một số nguyên Số $2$ là một số hữu tỉ Số $2$ là một số thực Số $2$ là một phân số Số $2$ là một số thập phân hữu hạn Số $2$ là một số thập phân vô hạn tuần hoàn

Trường hợp 4 và Trường hợp 5 dễ nhầm lẫn nên bạn cần chú ý đến chúng nhiều hơn. Tham khảo bảng bên dưới để có thêm thông tin

Khi rơi vào Trường hợp 4 thì cần thực hiện một hoặc một vài thủ thuật phù hợp với từng bài toán cụ thể mới có thể tìm ra đáp án

1.3 Chuyển số thập phân vô hạn tuần hoàn sang dạng thức mặc định của máy tính

Chuyển số thập phân vô hạn tuần hoàn 2.357575758 sang dạng thức mặc định của máy tính

Bước 1 Xác định phần nguyên, phần thập phân không tuần hoàn và phần thập phân tuần hoàn

Phần nguyên là $2$
Phần thập phân không tuần hoàn $3$
Phần thập phân tuần hoàn $57$

Bước 2 Nhập phần nguyên => nhấn phím => nhập phần thập phân không tuần hoàn => nhấn phím => nhập phần thập phân tuần hoàn

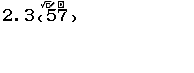
Bước 3 Nhấn phím =

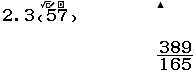
1.4 Ví dụ

Ví dụ 1.4.1

Tính $\lim \dfrac{3 n^{2}-n}{1+n^{2}}$

Bước 1 Nhập dãy số

Bước 2 Nhấn phím CALC => nhập $10^9$ => nhấn phím =

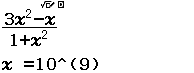
Bước 3 Quan sát kết quả ban đầu, chúng ta nhận thấy rơi vào Trường hợp 4 tức số thập phân vô hạn tuần hoàn

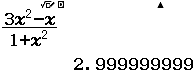
Số thập phân vô hạn tuần hoàn $2.(9)$ chuyển sang dạng thức hiển thị mặc định là $3$

Vậy giới hạn cần tìm là $3$

Ví dụ 1.4.2

Tính $\lim \dfrac{2.3+5^n}{13^n.11+7}$

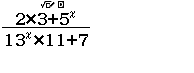
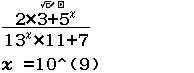
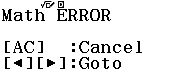
Giá trị cần tính toán vượt quá $10^{99}$ nên cần giảm giá trị xuống, cụ thể đối với bài này là $10^1$

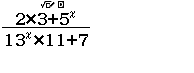
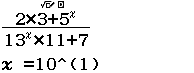
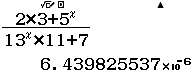
Vì kết quả ban đầu rơi vào Trường hợp 3 nên giới hạn cần tìm là $0$

2 Giới hạn của hàm số

2.1 Thuật giải

Bước 1 Nhập hàm số

Bước 2 Nhấn phím CALC => nếu giới hạn tiến tới

Trường hợp 1 $+\infty$ thì nhập $10^9$
Trường hợp 2 $-\infty$ thì nhập $-10^9$
Trường hợp 3 $a$ với $a \in R$ thì nhập $a+10^{-9}$ hoặc $a-10^{-9}$
Trường hợp 4 $a^{+}$ với $a \in R$ thì nhập $a+10^{-9}$
Trường hợp 5 $a^{-}$ với $a \in R$ thì nhập $a-10^{-9}$

Bước 3 Xem 1.1

2.2 Ví dụ

Ví dụ 2.2.1

Tính $\lim_{x \rightarrow -2} \dfrac{x^2-4}{x+2}$

Bước 1 Nhập hàm số

Bước 2 Nhấn phím CALC => nhập $-2+10^{-9}$ => nhấn phím =

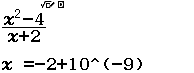
Bước 3 Quan sát kết quả ban đầu, chúng ta nhận thấy rơi vào Trường hợp 4 tức số thập phân vô hạn tuần hoàn

Vậy giới hạn cần tìm là $-4$

Ví dụ 2.2.2

Cho hàm số $f(x)=\left\{\begin{array}{l}5x+2 ~if~ x \geq 1 \\ x^{2}-3 ~if~ x<1 \end{array}\right.$

a) Tính $\lim_{x \rightarrow 1^-} f(x)$

b) Tính $\lim_{x \rightarrow 1^+} f(x)$

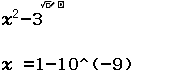
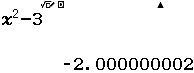
Vì kết quả ban đầu rơi vào Trường hợp 4 nên $\lim_{x \rightarrow 1^-} f(x) = -2.(0)=-2$

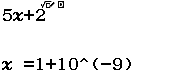
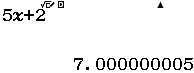
Vì kết quả ban đầu rơi vào Trường hợp 4 nên $\lim_{x \rightarrow 1^+} f(x) = 7.(0)=7$

Ví dụ 2.2.3

Tính $\lim_{x \rightarrow - \infty} \dfrac{2x+3}{x-1}$

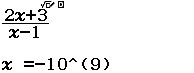
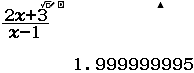
Vì kết quả ban đầu rơi vào Trường hợp 4 nên giới hạn cần tìm là $1.(9)=2$

Ví dụ 2.2.4

Tính $\lim_{x \rightarrow - \infty} (x^2-2x)$

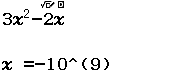
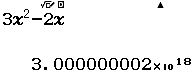
Vì kết quả ban đầu rơi vào Trường hợp 1 nên giới hạn cần tìm là $+\infty$

Ví dụ 2.2.5

Tính $\lim_{x \rightarrow 1^+} \dfrac{2x-3}{x-1}$

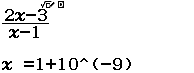
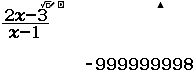
Vì kết quả ban đầu rơi vào Trường hợp 2 nên giới hạn cần tìm là $-\infty$

3 Hàm số liên tục

Xét tính liên tục của hàm số f(x) tại $x_0$

Bước 1 Tính $\lim_{x \rightarrow x_0} f(x)$

Bước 2 Tính $f(x_0)$

Bước 3 So sánh $\lim_{x \rightarrow x_0} f(x)$ và $f(x_0)$ nếu $\lim_{x \rightarrow x_0} f(x)=f(x_0)$ thì hàm số đã cho liên tục tại $x_0$

Ví dụ 3

Xét tính liên tục của hàm số $f(x)=\dfrac{x}{x-2}$ tại $x_0=3$

Bước 1 Tính $\lim_{x \rightarrow 3} \dfrac{x}{x-2}$

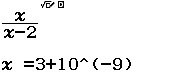
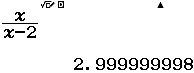
Bước 2 Tính $f(3)$

Vì $\lim _{x \rightarrow 3} \dfrac{x}{x-2}=3=f(3)$ nên hàm số đã cho liên tục tại $x_0=3$

4 Đường tiệm cận

Tìm đường tiệm cận ngang của đồ thị hàm số f(x)

Bước 1 Nếu $\lim _{x \rightarrow+\infty}f(x)=y_{0}$ thì $y={y_0}$ là đường tiệm cận ngang

Bước 2 Nếu $\lim _{x \rightarrow-\infty}f(x)=y_{0}$ thì $y={y_0}$ là đường tiệm cận ngang

Ví dụ 4.1

Tìm đường tiệm cận ngang của hàm số $f(x)=\dfrac{1}{\sqrt{x}}+1$

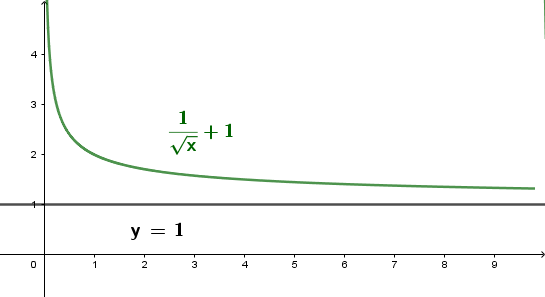
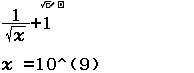
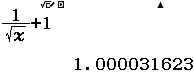
Vì $\lim _{x \rightarrow+\infty} \dfrac{1}{\sqrt{x}}+1=1$ nên hàm số đã cho có đường tiệm cận ngang là $y=1$

Tìm đường tiệm cận đứng đồ thị hàm số $f(x)=\dfrac{g(x)}{h(x)}$

Bước 1 Giả sử $x_1, x_2, x_3, …, x_n$ là nghiệm của phương trình $h(x)=0$

Bước 2 Xét $x_1$

Bước 2.1 Nếu $\lim _{x \rightarrow x_{1}^{+}} f(x)=+\infty$ hoặc $-\infty$ thì $x=x_1$ là đường tiệm cận đứng

Bước 2.2 Nếu $\lim _{x \rightarrow x_{1}^{-}} f(x)=+ \infty$ hoặc $-\infty$ thì $x=x_1$ là đường tiệm cận đứng

Chú ý 4.2

Nếu ở Bước 2.1 tìm được đường tiệm cận đứng thì bỏ qua Bước 2.2

Bước 3 Thực hiện tương tự Bước 2 với trường hợp $x_2$ và với các trường hợp còn lại (nếu có)

Ví dụ 4.2

Tìm đường tiệm cận đứng của đồ thị hàm số $f(x)=\dfrac{x-1}{x+2}$

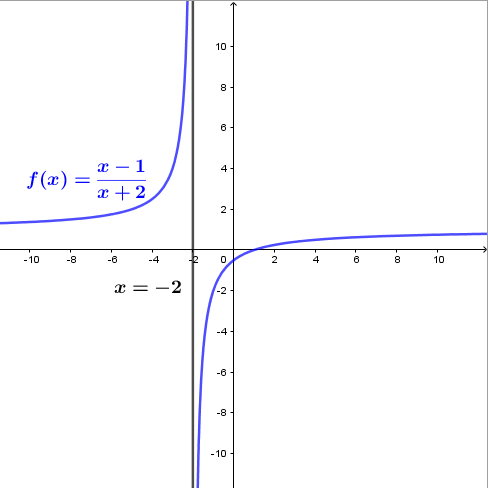
Bước 1 Giải $x+2=0 \Leftrightarrow x=-2$

Bước 2 Tính $\lim_{x \rightarrow -2^+} \dfrac{x-1}{x+2}$

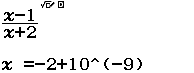
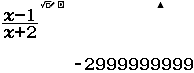
Vì $\lim _{x \rightarrow-2^{+}} \dfrac{x-1}{x+2}=-\infty$ nên đường tiệm cần đứng của hàm số đã cho là $x=-2$

5 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia

Câu 6, Đề thi tham khảo, Năm 2021

Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x+4}{x-1}$ là đường thẳng

A. $x=1$

B. $x=-1$

C. $x=2$

D. $x=-2$

Bước 1 Giải $x-1=0 \Leftrightarrow x=1$

Bước 2 Tính $\lim_{x \rightarrow 1^+} \dfrac{2x+4}{x-1}$

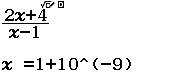
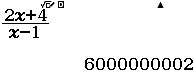
Vậy $x=1$ là đường tiệm cận đứng cần tìm

Câu 27, Đề thi tham khảo, Năm 2020

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{5x^2-4x-1}{x^2-1}$ là

A. $0$

B. $1$

C. $2$

D. $3$

Bước 1 Tính $\lim_{x \rightarrow + \infty} \dfrac{5x^2-4x-1}{x^2-1}$

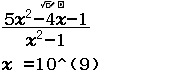
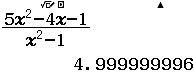
Suy ra $y=5$ là đường tiệm cận ngang của đồ thì hàm số đã cho

Bước 2 Giải $x^2-1=0 \Leftrightarrow x= \pm 1$

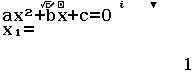
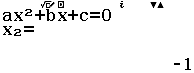
Bước 3 Tính

$\lim_{x \rightarrow 1^+} \dfrac{5x^2-4x-1}{x^2-1}$

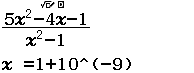
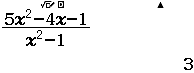
$\lim_{x \rightarrow 1^-} \dfrac{5x^2-4x-1}{x^2-1}$

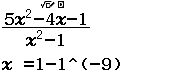
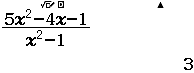
$\lim_{x \rightarrow -1^+} \dfrac{5x^2-4x-1}{x^2-1}$

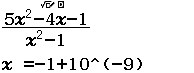
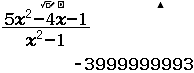
Suy ra $x=-1$ là đường tiệm cận đứng của đồ thị hàm số đã cho

Vậy đồ thị hàm số đã cho có 2 đường tiệm cận

Câu 13, Mã đề thi 101, Năm 2018

$\lim \dfrac{1}{5n+3}$ bằng

A. $0$

B. $\dfrac{1}{3}$

C. $+ \infty$

D. $\dfrac{1}{5}$

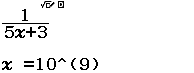
Vì kết quả ban đầu rơi vào Trường hợp 2 nên giới hạn cần tìm là $0$

Câu 18, Mã đề thi 101, Năm 2018

Số tiệm cận đứng của đồ thị hàm số $y=\dfrac{\sqrt{x+9}-3}{x^2+x}$ là

A. $3$

B. $2$

C. $0$

D. $1$

Câu 12, Mã đề thi 101, Năm 2017

Tìm số tiệm cận đứng của đồ thị hàm số $\dfrac{x^2-3x-4}{x^2-16}$

A. $2$

B. $3$

C. $1$

D. $0$

Bài viết cùng Serie<< Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi Trung học Phổ thông Quốc giaTính đạo hàm của hàm số bằng máy tính Casio fx-580VN X >>

Màn hình hiển thị	Nhận xét
$2.999999999$ $-4$ $-2.00000002$ $0.499999567$ $0.250000003$ $2.357575758$	Trường hợp 4 Số thập phân vô hạn tuần hoàn
$1.414213562$ $3.141592654$ $2.718281828$	Trường hợp 5 Số thập phân vô hạn không tuần hoàn