Tính toán số phức bằng máy tính cầm tay CASIO fx 580 VN X

Tính năng Complex của máy tính cầm tay CASIO fx 580 VN X cho phép chúng ta thực hiện các phép tính với các số phức một cách chính xác và nhanh chóng

Các phép tính được hỗ trợ là cộng, trừ, nhân, chia; lũy thừa, khai căn bậc hai; acgumen, số phức liên hợp; phần thực, phần ảo, môđun; …

1 Tính năng số phức

Muốn nhập được các số phức, muốn thực hiện được các phép toán với các số phức công việc đầu tiên bạn cần làm là mở tính năng số phức

Nhấn phím HOME => nhấn phím 2 để chọn Complex để mở tính năng số phức

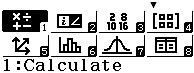
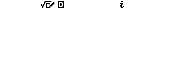
Nhấn phím ENG để nhập đơn vị ảo i

2 Cộng, trừ, nhân và chia số phức

Chẳng hạn mình cần tính tổng, hiệu, tích, thương của số phức 2+3i và 5+7i thì thực hiện tuần tự theo các bước bên dưới

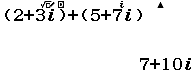
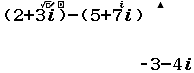
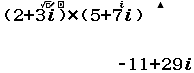
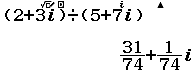
Xem thêm Cộng, trừ, nhân, chia số phức

3 Lũy thừa số phức

Chẳng hạn mình cần bình phương và lập phương số phức 3+4i thì thực hiện tuần tự theo các bước bên dưới

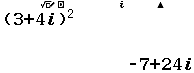
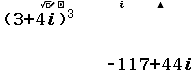
4 Khai căn bậc hai số phức

Chẳng hạn mình cần khai căn bậc hai của số phức 3+4i thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím => nhấn phím SHIFT => nhấn phím ( => nhập 3+4i

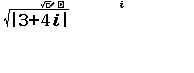
Bước 2

Bước 2.1 nhấn phím  => nhấn phím  => nhập  => nhấn phím 

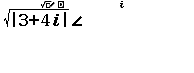
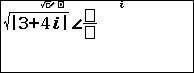
Bước 2.2 nhấn phím OPNT => nhấn phím 1 để chọn Argument

Bước 2.3 nhập 3+4i => nhấn phím ) => nhấn phím  => nhập 2

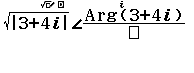
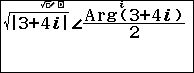
Bước 3 nhấn phím =

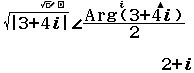
Vậy căn bậc hai của số phức 3+4i là 2+i và -2-i

Xem thêm Lũy thừa, khai căn bậc hai số phức

5 argument số phức

Chẳng hạn mình cần tìm argument của số phức thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím OPTN => nhấn phím 1 để chọn Argument

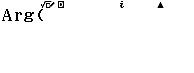
Bước 2 nhập số phức => nhấn phím =

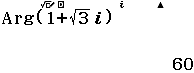
6 Số phức liên hợp

Chẳng hạn mình cần tìm số phức liên hợp của số phức 2+3i thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím OPTN => nhấn phím 2 để chọn Conjugate

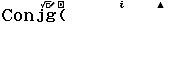
Bước 2 nhập 2+3i => nhấn phím =

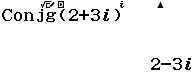
Xem thêm Acgumen, số phức liên hợp

7 Phần thực và phần ảo số phức

Chẳng hạn mình cần tìm phần thực và phần ảo của số phức 2+3i thì thực hiện tuần tự theo các bước bên dưới

Tìm phần thực

Bước 1 nhấn phím OPTN => nhấn phím 3 để chọn Real Part

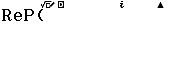
Bước 2 nhập 2+3i => nhấn phím =

Tìm phần ảo

Bước 1 nhấn phím OPTN => nhấn phím 4 để chọn Imaginary Part 

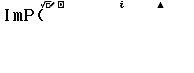
Bước 2 nhập 2+3i => nhấn phím =

8 Mô đun của số phức

Chẳng hạn mình cần tìm mô đun của số phức thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím SHIFT => nhấn phím (

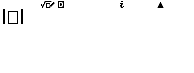
Bước 2 nhập => nhấn phím =

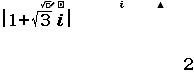
Xem thêm Phần thực, phần ảo, môđun số phức

9 Lời kết

Tính năng số phức / Complex của máy tính cầm tay CASIO fx 580 VN X còn cho phép chúng ta

• Chuyển đổi số phức từ dạng đại số sang dạng lượng giác
• Chuyển đổi số phức từ dạng lượng giác sang dạng đại số
• Khai căn bậc ba, bậc bốn, bậc n số phức
• Chuyển đổi số phức từ dạng đại số sang dạng mũ

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo