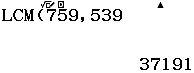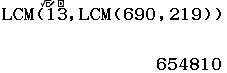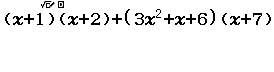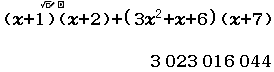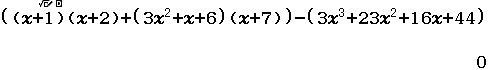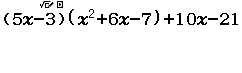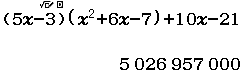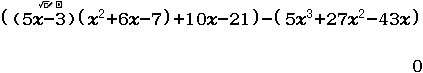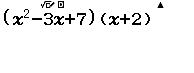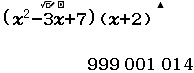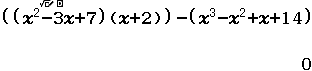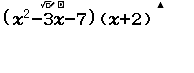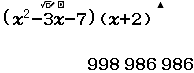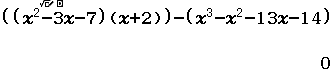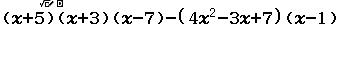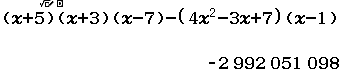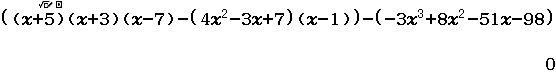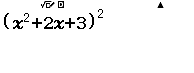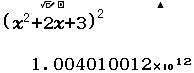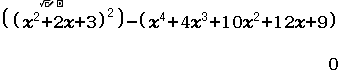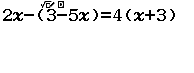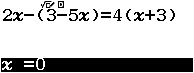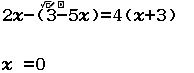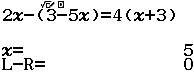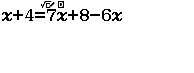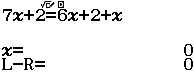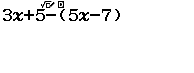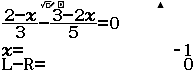Ứng dụng máy tính Casio fx-580VN X vào chương trình Toán THCS

Xin chào tất cả các bạn

Số lớn nhất mà máy tính cầm tay CASIO fx 580 VN X có thể phân tích được thành thừa số nguyên tố là 9 999 999 999

Ngoài ra số nào rơi vào một trong hai trường hợp bên dưới thì cũng không thể phân tích được cho dù có nhỏ hơn hoặc bằng 9 999 999 999

• Một thừa số trong các thừa số nguyên tố có giá trị từ 1 018 081 tức $1009^2$ trở lên
• Hai, ba, bốn, … thừa số trong các thừa số nguyên tố có nhiều hơn ba chữ số

Lúc bấy giờ phần không thể phân tích được sẽ nằm trong dấu ngoặc đơn

Muốn biết được phần không thể phân tích là số nguyên tố hay hợp số chúng ta phải tiến hành kiểm tra bằng kiến thức Toán học hoặc kiến thức máy tính cầm tay

Tạm gác lại việc kiểm tra bằng kiến thức Toán học, hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước kiểm tra một số tự nhiên lớn hơn hai là số nguyên tố hay là hợp số bằng máy tính cầm tay CASIO fx 580 VN X

Xem thêm Phân tích một số ra thừa số nguyên tố

1 Các bước kiểm tra

Bước 1 gán số cần kiểm tra vào biến nhớ x

Bước 2 tính giá trị biểu thức $\frac{x}{Int(\sqrt{x})}$ để biết khi nào dừng nhấn phím =

Nhấn phím ALPHA => nhấn phím + để nhấn phím Int

Bước 3 gán số cần kiểm tra vào bộ nhớ trả lời Ans

Bước 4

• Nhập biểu thức $\frac{x}{x \div Ans + 2}$ vào máy tính cầm tay
• Vừa nhấn phím = vừa quan sát xem có giá trị nào nguyên hay không, nếu không có giá trị nào nguyên thì số cần kiểm tra là số nguyên tố
• Việc nhấn phím = sẽ dừng lại khi gặp giá trị ở Bước 2

3 Thực hành kiểm tra

Chẳng hạn mình cần kiểm tra số $1~018~097$ là số nguyên tố hay là hợp số thì thực hiện tuần tự theo các bước bên dưới

Bước 1 gán số $1~018~097$ vào biến nhớ x

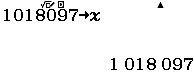
Bước 2 nhập biểu thức $\frac{x}{Int(\sqrt{x})}$ => nhấn phím =

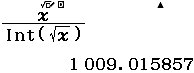
Suy ra chúng ta sẽ dừng nhấn phím = khi gặp giá trị $1~009.015857$

Bước 3 nhấn phím x => nhấn phím =

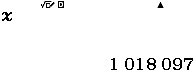
Bước 4

Nhập biểu thức $\frac{x}{x \div Ans + 2}$ => nhấn phím = liên tục đến khi nào gặp giá trị $1~009.015857$

Dễ thấy từ phím = đầu tiên đến phím = cuối cùng không có giá trị nào nguyên nên số $1~018~097$ là số nguyên tố

3 Lời kết

Chúng ta có nhu cầu kiểm tra một số tự nhiên lớn hơn hai là số nguyên tố hay là hợp số bằng máy tính cầm tay CASIO fx 580 VN X khi số này có giá trị rất lớn hoặc rơi vào các trường hợp mà máy tính cầm tay không thể phân tích được

Trong thực hành, hầu hết các trường hợp khi cần kiểm tra một số là số nguyên tố hay là hợp số chúng ta chỉ cần nhập số vào máy tính cầm tay và nhấn phím SHIFT rồi nhấn phím là xong

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

Xin chào tất cả các bạn

Hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước tìm ước chung lớn nhất, bội chung nhỏ nhất của hai số, ba số, bốn số, …, bằng máy tính cầm tay CASIO fx 580 VN X

1 Ước chung lớn nhất

Để tìm ước chung lớn nhất của hai số $a_1, a_2$ ta sử dụng phím GCD với công thức $GCD(a_1, a_2)$

Để tìm ước chung lớn nhất của ba số $a_1, a_2, a_3$ ta sử dụng phím GCD với công thức $GCD(a_1, GCD(a_2, a_3))$

Chẳng hạn 1 mình cần tìm ước chung lớn nhất của hai số $479, 686$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím ALPHA => nhấn phím $\times$

Bước 2 nhập số $479$

Bước 3 nhấn phím SHIFT => nhấn phím )

Bước 4 nhập số $686$

Bước 5 nhấn phím =

Vậy $UCLN(479, 686)=1$

Chẳng hạn 2 mình cần tìm ước chung lớn nhất của ba số $909, 153, 773$ thì thực hiện tuần tự theo các bước bên dưới

Vậy $UCLN(909, 153, 773)=1$

Xem thêm Ước chung lớn nhất

2 Bội chung nhỏ nhất

Để tìm bội chung nhỏ nhất của hai số $a_1, a_2$ ta sử dụng phím LCM với công thức $LCM(a_1, a_2)$

Để tìm bội chung nhỏ nhất của ba số $a_1, a_2, a_3$ ta sử dụng phím LCM với công thức $LCM(a_1, LCM(a_2, a_3))$

Chẳng hạn 3 mình cần tìm bội chung nhỏ nhất của hai số $759, 539$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhấn phím ALPHA => nhấn phím $\div$

Bước 2 nhập số $759$

Bước 3 nhấn phím SHIFT => nhấn phím )

Bước 4 nhập số $539$

Bước 5 nhấn phím =

Vậy $BCNN(759, 539)=37~191$

Chẳng hạn 4 mình cần tìm bội chung nhỏ nhất của ba số $13, 690, 219$ thì thực hiện tuần tự theo các bước bên dưới

Vậy $BCNN(13, 690, 219)=654~810$

Xem thêm Bội chung nhỏ nhất

3 Lời kết

Phím GCD và LCM của máy tính cầm tay CASIO fx 580 VN X mặc dù cho phép chúng ta xác định nhanh ước chung lớn nhất và bội chung nhỏ nhất của hai số, ba số, bốn số, …

Tuy nhiên với những số có giá trị lớn thì bạn nên tìm ước chung lớn nhất bằng thuật giải Euclid sau đó áp dụng công thức $LCM(A, B)=\frac{AB}{GCD(A, B)}$ để tìm bội chung nhỏ nhất

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

Xin chào tất cả các bạn, hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước thực hiện thủ thuật khai triển và rút gọn đa thức một ẩn với hệ số nguyên bằng máy tính cầm tay CASIO fx 580 VN X

Như các bạn đã viết, thao tác khai triển và rút gọn đa thức là một trong những thao tác thường nhất trong quá trình làm toán

Thao tác trên tuy không khó khăn nhưng với những đa thức phức tạp thì cũng tốn khá nhiều thời gian và công sức

Lúc bấy giờ, việc khai triển và rút gọn đa thức bằng máy tính cầm tay sẽ là một giải pháp tối ưu

1 Bật dấu phân cách ba chữ số

Khi dấu phân cách ba chữ số được bật thì kết quả tính toán sẽ tự động được tách thành từng bộ ba theo chiều từ phải sang trái

Bước 1 nhấn phím SHIFT => nhấn phím MENU

Bước 2 nhấn phím  => nhấn phím

Bước 3 nhấn phím 4

Bước 4 nhấn phím 1

2 Các bước khai triển và rút gọn

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích giá trị và dự đoán đa thức cần tìm

Bước 3.1 phân tích giá trị theo chiều từ phải sang trái theo nguyên tắc nếu có một bộ ba lớn bất thường thì lấy 1000 trừ cho bộ ba đó đồng thời cộng 1 vào bộ ba ngay bên trái

Bước 3.2 dự đoán đa thức cần tìm

Bước 4 nhập “đa thức đã cho trừ đa thức cần tìm” => nhấn phím CALC => nhấn phím SHIFT => nhấn phím . => nhấn phím = => nhấn phím =

• Nếu kết quả bằng 0 thì dự đoán chính xác
• Nếu kết quả khác 0 thì dự đoán không chính xác

3 Thực hành khai triển và rút gọn

Ví dụ 1 khai triển và rút gọn đa thức $(x+1)(x+2)+(3x^2+x+6)(x+7)$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $3~023~016~044$ được phân tích thành $3~23~16~44$
• $3x^3+23x^2+16x+44$

Bước 4 kiểm tra

Vậy $(x+1)(x+2)+(3x^2+x+6)(x+7)=3x^3+23x^2+16x+44$

Ví dụ 2 Khai triển và rút gọn đa thức $(5x-3)(x^2+6x-7)+10x-21$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $5~026~957~000$ được phân tích thành $5~~~026+1~~~957-1000~~~000$ hay $5~27~-43~0$
• $5x^3+27x^2-43x$

Bước 4 kiểm tra

Vậy $(5x-3)(x^2+6x-7)+10x-21=5x^3+27x^2-43x$

Ví dụ 3 Khai triển và rút gọn đa thức $(x^2-3x+7)(x+2)$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $999~001~014$ được phân tích thành $1~~~999-1000~~~001~~~014$ hay $1~-1~1~14$
• $x^3-x^2+x+14$

Bước 4 kiểm tra

Vậy $(x^2-3x+7)(x+2)=x^3-x^2+x+14$

Ví dụ 4 Khai triển và rút gọn đa thức $(x^2-3x-7)(x+2)$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $998~986~986$ được phân tích thành $1~~~998+1-1000~~~986+1-1000~~~986-1000$ hay $1~-1~-13~-14$
• $x^3-x^2-13x-14$

Bước 4 kiểm tra

Vậy $(x^2-3x-7)(x+2)=x^3-x^2-13x-14$

Ví dụ 5 Khai triển và rút gọn đa thức $(x+5)(x+3)(x-7)-(4x^2-3x+7)(x-1)$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $2~992~051~098$ được phân tích thành $2+1~~~992-1000~~~051~~~098$ hay $3~-8~51~98$
• Vì giá trị tìm được ở Bước 2 nhỏ hơn không nên kết quả phân tích cuối cùng phải là $-3~8~-51~-98$
• $-3x^3+8x^2-51x-98$

Bước 4 kiểm tra

Vậy $(x+5)(x+3)(x-7)-(4x^2-3x+7)(x-1)=-3x^3+8x^2-51x-98$

Ví dụ 6 Khai triển và rút gọn đa thức $(x^2+2x+3)^2$

Bước 1 nhập đa thức

Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =

Bước 3 phân tích và dự đoán

• $1.004010012 \times 10^{12} =1~004~010~012~009$ được phân tích thành $1~4~10~12~9$
• $x^4+4x^3+10x^2+12x+9$

Xem thêm Xử lý kết quả tính toán tràn màn hình

Bước 4 kiểm tra

Vậy $(x^2+2x+3)^2=x^4+4x^3+10x^2+12x+9$

4 Lời kết

Mặc dù thủ thuật khai triển và rút gọn đa thức trên máy tính cầm tay CASIO fx 580 VN X chỉ áp dụng được với những đa thức một biến và có hệ số nguyên nhưng đây vẫn là một thủ thuật tuyệt với

Trong thời gian tới mình sẽ nghiên cứu và phát triển thêm thủ thuật này theo hướng áp dụng được cho các đa thức một biến có hệ số hữu tỉ hoặc đa thức hai biến

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

Nguyên tác

Trần Ngọc Ánh Phương

Phím SOLVE của máy tính cầm tay CASIO fx 580 VN X cho phép chúng ta dò tìm nghiệm của một phương trình bất kì

Tuy nhiên, do những hạn chế của phím này, với mỗi loại phương trình (phương trình đa thức, phương trình phân thức, phương trình vô tỉ, …) chúng ta cần thực hiện thêm một số thao tác phù hợp

Dưới đây là chi tiết các bước sử dụng phím SOLVE của máy tính cầm tay CASIO fx 580 VN X giải nhanh phương trình bậc nhất một ẩn hoặc phương trình quy về phương trình bậc nhất một ẩn

1 Định nghĩa phương trình bậc nhất một ẩn

Phương trình có dạng $ax+b=0$ với $a$, $b$ là hai số đã cho và $a \neq 0$ được gọi là phương trình bậc nhất một ẩn

Phương trình quy về phương trình bậc nhất một ẩn chỉ các phương trình mà hai về của chúng là hai biểu thức hữu tỉ của ẩn, không chứa ẩn ở mẫu và có thể đưa về dạng $ax+b=0$

2 Các bước giải

Bước 1 nhập phương trình vào máy tính cầm tay

Bước 2 nhấn phím SHIFT => nhấn phím CALC

Bước 3 nhập giá trị ban đầu, mình thường nhập $0$

Bước 4 nhấn phím =

Bước 5 nhấn phím =

3 Thực hành giải

Chẳng hạn 1 mình cần giải phương trình $2x-(3-5x)=4(x+3)$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 nhập phương trình $2x-(3-5x)=4(x+3)$ vào máy tính cầm tay

Bước 2 nhấn phím SHIFT => nhấn phím CALC

Bước 3 nhập giá trị ban đầu, ở đây mình sẽ nhập $0$

Bước 4 nhấn phím =

Bước 5 nhấn phím =

Vậy phương trình đã cho có một nghiệm duy nhất là $x=5$

Chẳng hạn 2 mình cần giải phương trình $x+4=7x+8-6x$ thì thực hiện tuần tự theo các bước bên dưới

Vì chúng ta đang dò tìm nghiệm của các phương trình bậc nhất một ẩn hoặc phương trình quy về phương trình bậc nhất một ẩn nên thì thông báo Cannot Solve gần như đồng nghĩa với phương trình vô nghiệm

Vậy phương trình đã cho vô nghiệm

Chẳng hạn 3 mình cần giải phương trình $7x+2=6x+2+x$ thì thực hiện tuần tự theo các bước bên dưới

Vậy phương trình đã cho có một nghiệm duy nhất là $x=0$

Kết luận trên là sai hoàn toàn vì phương trình đã cho có vô số nghiệm, thật vậy $7x+2=6x+2+x \Leftrightarrow 7x-6x-x=2-2 \Leftrightarrow 0x=0$

Một số phương trình quy về phương trình bậc nhất một ẩn có thể rơi vào trường hợp có vô số nghiệm

Để tránh sai sót không đáng có, khi dò tìm được nghiệm bằng $0$ chúng ta nên dò tìm thêm một lần nữa với một giá trị ban đầu khác

• Nếu nghiệm tìm được vẫn là $0$ thì kết luận phương trình đã có một nghiệm duy nhất là $x=0$
• Nếu nghiệm tìm được là một số khác $0$ thì kết luận phương trình đã cho có vô số nghiệm

4 Lời kết

Nhờ vào việc sử dụng thành thạo phím SOLVE của máy tính cầm tay CASIO fx 580 VN X mà chúng ta đã tìm được tập nghiệm của phương trình nhất một ẩn hoặc phương trình quy về phương trình bậc nhất một ẩn một cách chính xác và nhanh chóng

Trường hợp cần giải phương trình bậc hai, phương trình bậc ba và phương trình bậc bốn thì các bạn nên sử dụng tính năng Equation các bạn nhá

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

Không biết vì lí do gì mà máy tính cầm tay CASIO fx 580 VN X vẫn không hỗ trợ chúng ta giải bất phương trình bậc nhất một ẩn

Mặc dù việc giải bất phương trình này khá đơn giản nhưng ít nhiều cũng tốn thời gian, đặc biết là với các bất phương trình phức tạp

1 Định nghĩa bất phương trình bậc nhất một ẩn

Bất phương trình dạng $ax+b<0$ hoặc $ax+b>0$ hoặc $ax+b \geq 0$ hoặc $ax+b \leq 0$ với $a, b$ là hai số đã cho và $a \neq 0$ được gọi là bất phương trình bậc nhất một ẩn

2 Các bước giải

Bước 1 biến đổi sơ cấp sao cho vế phải của bất phương trình bằng không

Bước 2 nhập vế trái của bất phương trình vào máy tính cầm tay

Bước 3 nhấn phím CALC => nhập $10^9$ => nhấn phím = => nhấn phím =

• Nếu giá trị tìm được lớn hơn không thì dấu của tập nghiệm cùng chiều với dấu của bất phương trình
• Nếu giá trị tìm được nhỏ hơn không thì dấu của tập nghiệm ngược chiều với dấu của bất phương trình

Bước 4 sử dụng phím SOLVE giải phương trình bậc nhất tương ứng

3 Thực hành giải

Chẳng hạn mình cần giải bất phương trình $3x+5<5x-7$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 biến đổi sơ cấp $3x+5<5x-7 \Leftrightarrow 3x+5 –(5x-7) < 0$

Bước 2 nhập $3x+5 –(5x-7)$

Bước 3 nhấn phím CALC => nhập $10^9$ => nhấn phím = => nhấn phím =

Vì $-1999999988 < 0$ nên dấu của tập nghiệm là $>$

Bước 4 giải phương trình $3x+5 –(5x-7)=0$

Vậy tập nghiệm của bất phương trình đã cho là $x>6$

Chẳng hạn mình cần giải bất phương trình $\frac{2-x}{3}<\frac{3-2x}{5}$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 biến đổi sơ cấp $\frac{2-x}{3}<\frac{3-2x}{5} \Leftrightarrow \frac{2-x}{3}-\frac{3-2x}{5} < 0$

Bước 2 nhập $\frac{2-x}{3}-\frac{3-2x}{5}$

Bước 3 nhấn phím CALC => nhập $10^9$ => nhấn phím = => nhấn phím =

Vì $66666666.73 > 0$ nên dấu của tập nghiệm là $<$

Bước 4 giải phương trình $\dfrac{2-x}{3}-\dfrac{3-2x}{5}=0$

Vậy tập nghiệm của bất phương trình đã cho là $x<-1$

4 Lời kết

Bằng việc sử dụng kết hợp phím CALC và phím SOLVE của máy tính cầm tay CASIO fx 580 VN X mà chúng ta đã giải được bất phương trình bậc nhất một ẩn một cách chính xác và nhanh chóng

Riêng việc giải bất phương trình bậc hai, bậc ba, bậc bốn thì bạn hãy sử dụng tính năng Inequality

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo