Phép tính nâng cao của máy tính cầm tay CASIO fx 580 VN X
Xin chào tất cả các bạn, hôm nay, mình sẽ hướng dẫn các bạn sử dụng các phép tính nâng cao của máy tính cầm tay CASIO fx 580 VN X
Các phép tính nâng cao sẽ được thực hiện một cách chính xác và nhanh chóng thông qua các hàm của CASIO fx 580 VN X

1 Số π
Nhấn phím SHIFT => nhấn phím $\times 10^x$ để nhập số π vào máy tính cầm tay
Giá trị của số π hiển thị trên màn hình là 3,141592654 tuy nhiên giá trị tính toán là 3,14159265358980
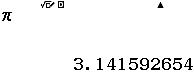
2 Số e
Nhấn phím ALPHA => nhấn phím $\times 10^x$ để nhập số e vào máy tính cầm tay
Giá trị của số e hiển thị trên màn hình là 2,718281828 tuy nhiên giá trị tính toán là 2,71828182845904
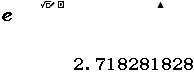
3 Hàm số lượng giác sin, cos, tan
Chẳng hạn mình cần tính giá trị lượng giác sin của 90 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 xác định đơn vị góc được cài đặt
Quan sát chỉ báo trên màn hình ta thấy có chỉ báo D có nghĩa là đơn vị góc đang được cài đặt là độ

Bước 2 nhấn phím sin => nhập 90 => nhấn phím =
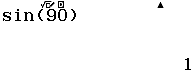
Xem thêm Giá trị lượng giác sin, cos, tan
4 Hàm số lượng giác ngược arcsin, arccos, arctan
Chẳng hạn mình cần tìm độ lớn của góc $\alpha$ biết giá trị lượng giác sin của góc $\alpha$ là $\frac{\sqrt{2}}{2}}$
Bước 1 nhấn phím SHIFT => nhấn phím $\sin^{-1}$

Bước 2 nhập $\frac{\sqrt{2}}{2}$ => nhấn phím =
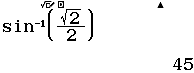
Xem thêm Hàm số lượng giác ngược arcsin, arccos, arctan
5 Phép toán logarit
Giả sử mình cần tính $\log_{159} 31$ thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Nhấn phím ![]() => nhập cơ số 159 => nhấn phím
=> nhập cơ số 159 => nhấn phím ![]() => nhập 31 => nhấn phím =
=> nhập 31 => nhấn phím =




Xem thêm Phép toán logarit, log và ln
6 Tích phân
Chẳng hạn mình cần tính tính phân $\int_1^2 x^2+2x+3 dx$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ![]()

Bước 2 nhập hàm số cần tính tích phân vào máy tính cầm tay
Bước 2.1 nhập hàm số dưới dấu tích phân $x^2+2x+3$
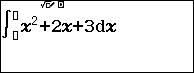
Bước 2.2 nhấn phím ![]() => nhập cận dưới 1
=> nhập cận dưới 1
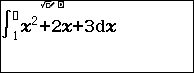
Bước 2.3 nhấn phím ![]() => nhập cận trên 2
=> nhập cận trên 2
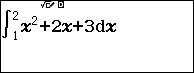
Bước 3 nhấn phím = để xem kết quả
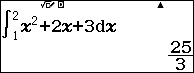
Xem thêm Tích phân
7 Đạo hàm tại một điểm
Chẳng hạn mình cần tính $f'(1)$ biết $f(x)=x^2+2x+3$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím ![]()
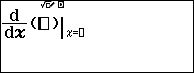
Bước 2 nhập hàm số và nhập điểm cần tính đạo hàm vào máy tính cầm tay
Bước 2.1 nhập $x^2+2x+3$ vào máy tính cầm tay
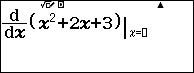
Bước 2.2 nhấn phím ![]()
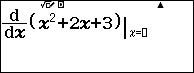
Bước 2.3 nhập 1
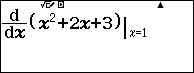
Bước 3 Nhấn phím = để xem kết quả
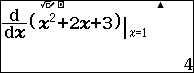
Xem thêm Đạo hàm tại một điểm
8 Tổng của dãy số
Chẳng hạn mình cần tính $\sum_1^{10} x^2+2x+3$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím x

Bước 2 nhập số hạng tổng quát $x^2+2x+3$
Vì máy tính cầm tay không có biến nhớ n nên chúng ta sẽ sử dụng biến nhớ x
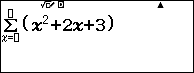
Bước 3 nhấn phím ![]() => nhập cận dưới 1
=> nhập cận dưới 1
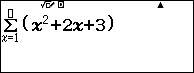
Bước 4 nhấn phím ![]() => nhập cận trên 10
=> nhập cận trên 10
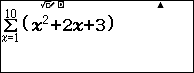
Bước 5 nhấn phím =
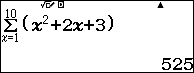
Xem thêm Tổng của dãy số
9 Tích của dãy số
Chẳng hạn mình cần tính $\prod_1^{10} x^2+2x+3$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím x

Bước 2 nhập $x^2+2x+3$
Vì máy tính cầm tay không có biến nhớ n nên chúng ta sẽ nhập biến nhớ x
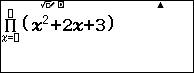
Bước 3 nhấn phím ![]() => nhập cận dưới 1
=> nhập cận dưới 1
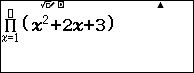
Bước 4 nhấn phím ![]() => nhập cận trên 10
=> nhập cận trên 10
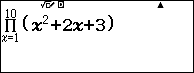
Bước 5 nhấn phím =
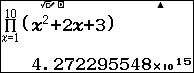
Vậy $\prod_1^{10} x^2+2x+3$ $=$ $4272295548416544$
Xem thêm Tích của dãy số
10 Pol – Tọa độ chữ nhật
Chẳng hạn mình cần chuyển tọa độ $(\sqrt{2}, \sqrt{2})$ sang tọa độ cực thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím +

Bước 2 nhập hoành độ $\sqrt{2}$

Bước 3 nhấn phím SHIFT => nhấn phím )

Bước 4 nhập trung độ $\sqrt{2}$

Bước 5 nhấn phím =
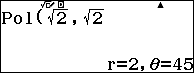
Xem thêm Pol chuyển đổi tọa độ chữ nhật sang tọa độ cực
11 Rec – Tọa độ cực
Chẳng hạn mình cần chuyển tọa độ $(\sqrt{2}, 45)$ sang tọa độ chữ nhật thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím –

Bước 2 nhập độ dài thẳng $\sqrt{2}$

Bước 3 nhấn phím SHIFT => nhấn phím )

Bước 4 nhập độ lớn góc 45

Bước 5 nhấn phím =

Xem thêm Rec chuyển đổi tọa độ cực sang tọa độ chữ nhật
12 ! – Giai thừa (hoán vị)
Chẳng hạn mình cần tính giai thừa, số các hoán vị của 9 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhập 9 vào máy tính cầm tay

Bước 2 nhấn phím SHIFT => nhấn phím $x^{-1}$

Bước 3 nhấn phím = để xem số các hoán vị / giai thừa của n phần tử

Xem thêm Giai thừa (hoán vị)
13 Abs – Giá trị tuyệt đối
Giả sử mình cần tính giá trị tuyệt đối của 647-79+127 thì thực hiện tuần tự theo các bước bên dưới …
Bước 1 nhấn phím SHIFT => nhấn phím (

Bước 2 nhập 647-79+127 vào máy tính cầm tay

Bước 3 nhấn phím = để xem kết quả

Xem thêm Giá trị tuyệt đối
14 Ran# – Số ngẫu nhiên
Chẳng hạn mình cần tạo ra một số ngẫu nhiên từ 0.000 đến 0.999 thực hiện hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím ![]()

Bước 2 nhấn phím =



15 RanInt – Số nguyên ngẫu nhiên
Chẳng hạn mình cần tạo một số nguyên ngẫu nhiên có hai chữ số thì thực hiện tuần tự theo các bước bên dưới
Dễ thấy số nguyên ngẫu nhiên cần tạo thuộc đoạn từ 10 đến 99
Bước 1 nhấn phím ALPHA => nhấn phím ![]()

Bước 2 nhập 10 => nhấn phím SHIFT => nhấn phím ) => nhập 99



Bước 3 nhấn phím =



Xem thêm Số ngẫu nhiên, số nguyên ngẫu nhiên
16 nPr – Chỉnh hợp
Chẳng hạn mình cần tính số các chỉnh hợp chập 7 của 9 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhập 9 vào máy tính cầm tay

Bước 2 nhấn phím SHIFT => nhấn phím $\times$

Bước 3 nhập 7 vào máy tính cầm tay

Bước 4 nhấn phím = để xem số các chỉnh hợp chập k của n phần tử

Xem thêm Chỉnh hợp
17 nCr – Tổ hợp
Chẳng hạn mình cần tính số các tổ hợp chập 3 của 33 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhập 33 vào máy tính cầm tay

Bước 2 nhấn phím SHIFT => nhấn phím $\div$

Bước 3 nhập 3 vào máy tính cầm tay

Bước 4 nhấn phím = để xem số các tổ hợp chập k của n phần tử

Xem thêm Tổ hợp
18 GCD – Ước chung lớn nhất
Chẳng hạn mình cần tìm ước chung lớn nhất của 213 của 947 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím $\times$

Bước 2 nhập 213 => nhấn phím SHIFT => nhấn phím ) => nhập 947



Bước 3 nhấn phím = để xem kết quả

Xem thêm Ước chung lớn nhất
19 LCM – Bội chung nhỏ nhất
Chẳng hạn mình cần tìm bội chung nhỏ nhất của 213 của 947 thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím $\div$

Bước 2 nhập 213 => nhấn phím SHIFT => nhấn phím ) => nhập 947



Bước 3 nhấn phím = để xem kết quả

Xem thêm Bội chung nhỏ nhất
20 Int – Số nguyên của giá trị
Chẳng hạn mình cần lấy phần nguyên của $\sqrt{34}$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím +

Bước 2 nhập $\sqrt{34}$

Bước 3 nhấn phím =

21 Intg – Số nguyên lớn nhất không vượt quá giá trị
Chẳng hạn mình cần xác định số nguyên lớn nhất không vượt quá giá trị $-\sqrt{349}$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím –

Bước 2 nhập $-\sqrt{349}$

Bước 3 nhấn phím =

Xem thêm Phần nguyên của giá trị, số nguyên lớn nhất không vượt quá giá trị (hàm phần nguyên)
22 Hằng số khoa học
Chẳng hạn mình cần tra cứu vận tốc ánh sáng trong chân không thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím SHIFT => nhấn phím 7

Bước 2 nhấn phím 1 để chọn Universal
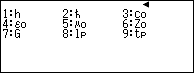
Bước 3 nhấn phím 3 để chọn $C_o$ tức hằng số vận tốc ánh sáng trong chân không

Bước 4 nhấn phím =

Xem thêm Tra cứu giá trị của các hằng số khoa học
23 Chuyển đổi đơn vị đo lường
Chẳng hạn mình cần chuyển đổi 179 in sang cm thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhập 197

Bước 2 nhấn phím SHIFT => nhấn phím 8 => nhấn phím 1 để chọn Length => nhấn phím 1 để chọn in▸cm



Bước 3 nhấn phím SHIFT => nhấn phím =

Xem thêm Chuyển đổi đơn vị đo lường
24 Lời kết
Đến đây mình đã hoàn thành công việc hướng dẫn sơ lược về các phép tính nâng cao trên máy tính cầm tay CASIO fx 580 VN X
Chi tiết và đầy đủ về cách sử dụng các tính nâng / các hàm bạn vui lòng nháy chuột vào liên kết tương ứng
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo