Xét vị trí tương đối của hai đường thẳng bằng máy tính CASIO fx-580VN X
Về phương diện vị trí hai đường thẳng trên mặt phẳng có ba vị trí tương đối là cắt nhau, song song và trùng nhau; hai đường thẳng trong không gian thì có thêm một vị trí nữa là chéo nhau
Đối với hai đường thẳng trên mặt phẳng chúng ta có thể xét vị trí tương đối của chúng bằng cách giải hệ hai phương trình hai ẩn
Đối với hai đường thẳng trong không gian chúng ta có thể xét vị trí tương đối của chúng bằng cách tính tích có hướng và tích hỗn hợp
Tất cả các công việc trên đều có thể thực hiện dễ dàng bằng máy tính CASIO fx-580VN X

1 Vị trí tương đối của hai đường thẳng trên mặt phẳng
1.1 Kiến thức Toán học
Trên mặt phẳng ![]() cho đường thẳng
cho đường thẳng ![]() và
và ![]() lần lượt có phương trình tổng quát là
lần lượt có phương trình tổng quát là ![]() và
và ![]()
Toạ độ giao điểm của ![]() và
và ![]() là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 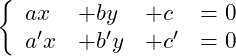
- Nếu hệ phương trình có một nghiệm duy nhất thì
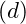 cắt
cắt 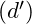
- Nếu hệ phương trình vô nghiệm thì
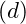 song song
song song 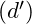
- Nếu hệ phương trình có vô số nghiệm thì
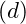 trùng
trùng 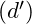
1.2 Thủ thuật máy tính CASIO fx-580VN X
Có nhiều thủ thuật để xác định vị trí tương đối của hai đường thẳng trên mặt phẳng như đa biểu thức, phương thức tính toán Verify, phương thức tính toán Equation/ Func, …
Trong đó thủ thuật sử dụng phương thức tính toán Equation/ Func tức giải hệ hai phương trình bậc nhất hai ẩn là tối ưu nhất
Nếu phương trình đường thẳng được cho dưới dạng tham số, đoạn chắn thì bạn cần chuyển về tổng quát trước khi áp dụng thủ thuật
Bước 1 Chọn phương thức tính toán Equation/ Func
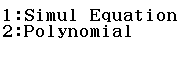
Bước 2 Chọn Simul Equation
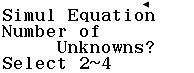
Bước 3 Nhấn phím 2
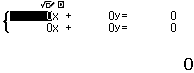
Bước 4 Nhập các hệ số của hệ phương trình
Bước 5 Nhấn phím =
- Nếu máy tính thông báo
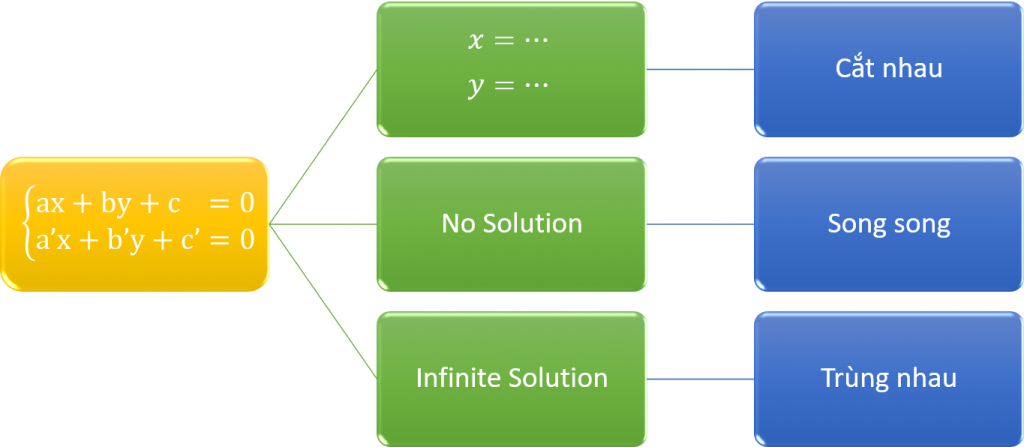
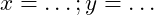 thì hai đường thẳng cắt nhau
thì hai đường thẳng cắt nhau - Nếu máy tính thông báo No Solution thì hai đường thẳng song song
- Nếu máy tính thông báo Infinite Solution thì hai đường thẳng trùng nhau
1.3 Ví dụ minh họa
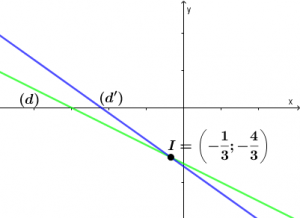
Xét vị trí tương đối của đường thẳng ![]() và đường thẳng
và đường thẳng ![]()
Bước 1 Nhập hệ phương trình 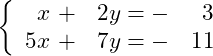
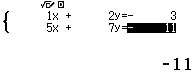
Bước 2 Nhấn phím =


Vậy ![]() cắt
cắt ![]() và tọa độ giao điểm là
và tọa độ giao điểm là 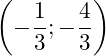
Xét vị trí tương đối của đường thẳng ![]() và đường thẳng
và đường thẳng ![]()
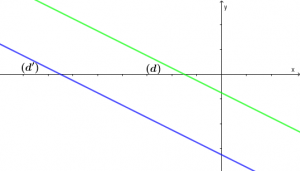
Bước 1 Nhập hệ phương trình 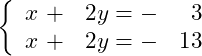
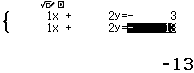
Bước 2 Nhấn phím =
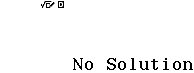
Vậy ![]() song song
song song ![]()
Xét vị trí tương đối của đường thẳng ![]() và đường thẳng
và đường thẳng ![]()
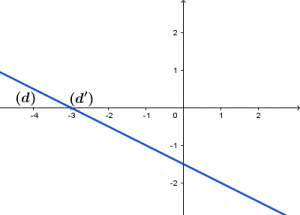
Bước 1 Nhập hệ phương trình 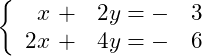
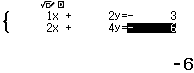
Bước 2 Nhấn phím =

Vậy ![]() trùng
trùng ![]()
2 Vị trí tương đối của hai đường thẳng trong không gian
2.1 Kiến thức Toán học
Trong không gian ![]() cho đường thẳng
cho đường thẳng ![]() đi qua điểm
đi qua điểm ![]() có véctơ chỉ phương
có véctơ chỉ phương ![]() và đường thẳng
và đường thẳng ![]() đi qua điểm
đi qua điểm ![]() có véctơ chỉ phương
có véctơ chỉ phương ![]()
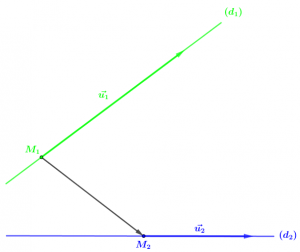
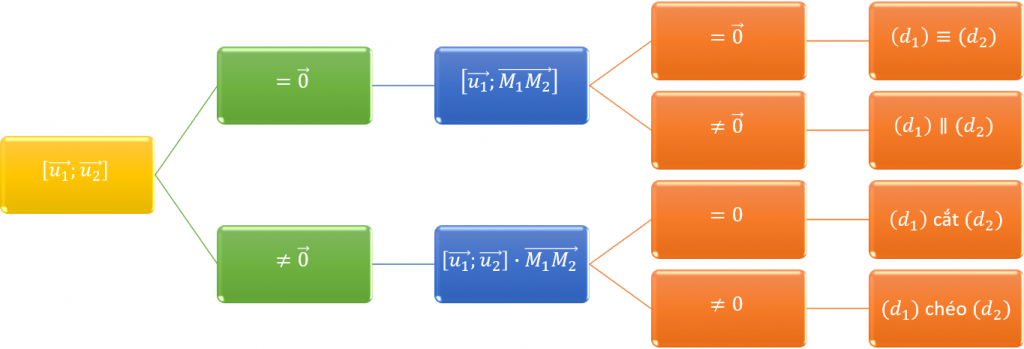
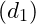 trùng
trùng 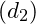 khi và chỉ khi
khi và chỉ khi ![Rendered by QuickLaTeX.com \left\{\begin{array}{ll}\left\mspace{1mu}[\vec{u_1}; \vec{u_2}\right]&=\vec{0}\\\left[\vec{u_1}; \overrightarrow{M_1M_2}\right]&=\vec{0}\end{array}\right.](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-20b6019c41c8fd622997f7b3f1ec8870_l3.png)
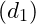 song song
song song 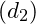 khi và chỉ khi
khi và chỉ khi ![Rendered by QuickLaTeX.com \left\{\begin{array}{ll}\left\mspace{1mu}[\vec{u_1}; \vec{u_2}\right]&=\vec{0}\\\left[\vec{u_1}; \overrightarrow{M_1M_2}\right]&\neq\vec{0}\end{array}\right.](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-00a5cc6f5241e06cc3af21529fd52507_l3.png)
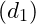 cắt
cắt 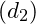 khi và chỉ khi
khi và chỉ khi ![Rendered by QuickLaTeX.com \left\{\begin{array}{ll}\left[\vec{u_1}; \vec{u_2}\right]&\neq\vec{0}\\\left[\vec{u_1}; \vec{u_2}\right]\cdot\overrightarrow{M_1M_2}&=0\end{array}\right.](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-8ff4fe0172bb5ec0b55aef556d6ce022_l3.png)
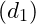 chéo
chéo 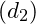 khi và chỉ khi
khi và chỉ khi ![Rendered by QuickLaTeX.com \left\{\begin{array}{ll}\left[\vec{u_1}; \vec{u_2}\right]&\neq\vec{0}\\\left[\vec{u_1}; \vec{u_2}\right]\cdot\overrightarrow{M_{1}M_{2}}&\neq0\end{array}\right.](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-72e6e865fc219d4511d445184001928b_l3.png)
![Rendered by QuickLaTeX.com [\vec{u_1}; \vec{u_2}]](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-b3c039b793c7a6ec45d972083f23dc0e_l3.png) được gọi là tích có hướng của
được gọi là tích có hướng của 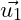 ,
, 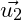
![Rendered by QuickLaTeX.com \left[\vec{u_1}; \vec{u_2}\right] \cdot \overrightarrow{M_1M_2}](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-abe076373735061536c06eeb6f9f36e4_l3.png) được gọi là tích hỗn hợp của
được gọi là tích hỗn hợp của 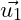 ,
, 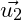 ,
, 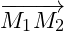
- Tích có hướng của hai véctơ là một véctơ
- Tích hỗn hợp của ba véctơ là một số
Các phép tính này đều có thể thực hiện dễ dàng nhờ vào phương thức tính toán Vector của máy tính CASIO fx-580VN nên bạn không cần bâng khuâng
2.2 Thủ thuật máy tính CASIO fx-580VN X
Bước 1 Chọn phương thức tính toán Vector

Bước 2 Định nghĩa ![]() ,
, ![]() ,
, ![]()
Bước 3 Tính ![]()
- Nếu
![Rendered by QuickLaTeX.com [\vec{u_1}; \vec{u_2}]=\vec{0}](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-babfbbbe159542f5e7a0d2edcd28f4f7_l3.png) thì tính
thì tính ![Rendered by QuickLaTeX.com [\vec{u_1}; \overrightarrow{M_1M_2}]](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-1f7594ef9da0fa841d8e24de1d7852aa_l3.png)
- Nếu
![Rendered by QuickLaTeX.com [\vec{u_1}; \vec{u_2}]\neq\vec{0}](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-598b988c473fd96f655838a3dff94a78_l3.png) thì tính
thì tính ![Rendered by QuickLaTeX.com [\vec{u_1}; \vec{u_2}] \cdot \overrightarrow{M_1 M_2}](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-8238fbb08fe7c94be01e6dee2a62aec9_l3.png)
Bước 4 Kết luận
- Nếu
![Rendered by QuickLaTeX.com [\vec{u_1}; \overrightarrow{M_1M_2}]=\vec{0}](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-4454816e95fc7616cc943784d98da196_l3.png) thì
thì 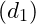 trùng
trùng 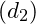 ngược lại
ngược lại 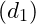 song song
song song 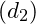
- Nếu
![Rendered by QuickLaTeX.com [\vec{u_1}; \vec{u_2}] \cdot \overrightarrow{M_1M_2}=0](https://nhutnguyenminh.com/wp-content/ql-cache/quicklatex.com-081b75800db15b7a10eb72badc0dca06_l3.png) thì
thì 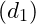 cắt
cắt 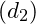 ngược lại
ngược lại 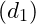 chéo
chéo 
2.3 Ví dụ minh họa
Xét vị trí tương đối của đường thẳng 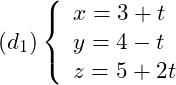 và đường thẳng
và đường thẳng 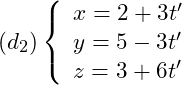
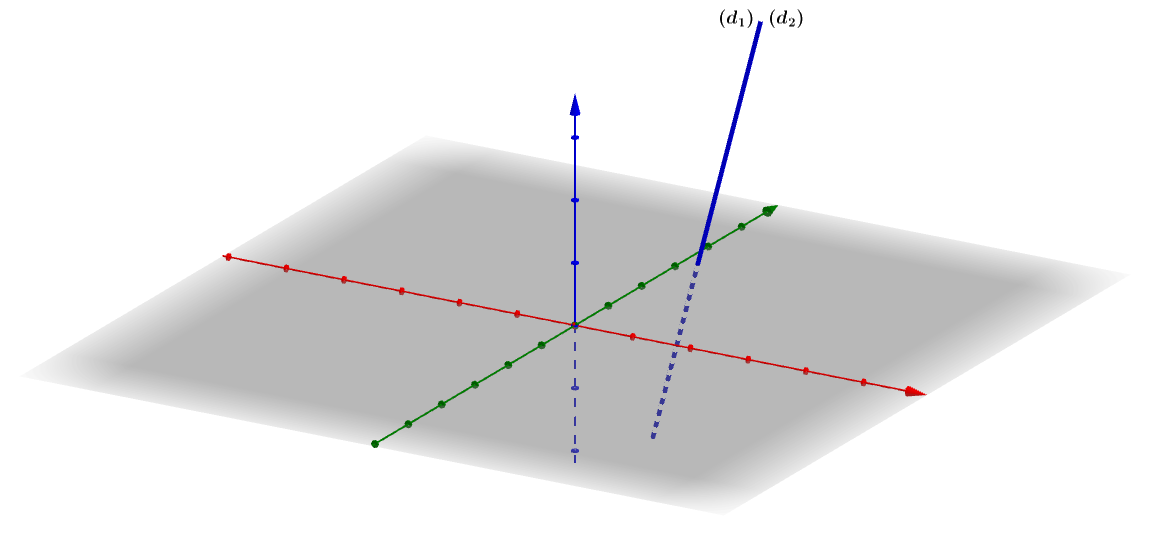
Dễ thấy ![]()
Bước 1 Chọn phương thức tính toán Vector

Bước 2 Khai báo ![]()
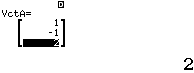
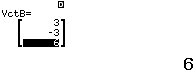
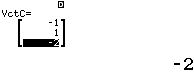
Bước 3 Tính tích có hướng ![]()
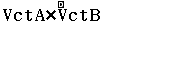
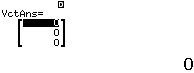
Suy ra ![]() và
và ![]() chỉ có thể trùng nhau hoặc song song
chỉ có thể trùng nhau hoặc song song
Bước 4 Tính tích có hướng ![]()
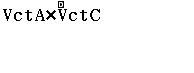
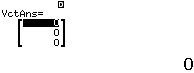
Vậy ![]() trùng
trùng ![]()
Xét vị trí tương đối của đường thẳng 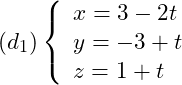 và đường thẳng
và đường thẳng 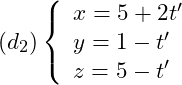
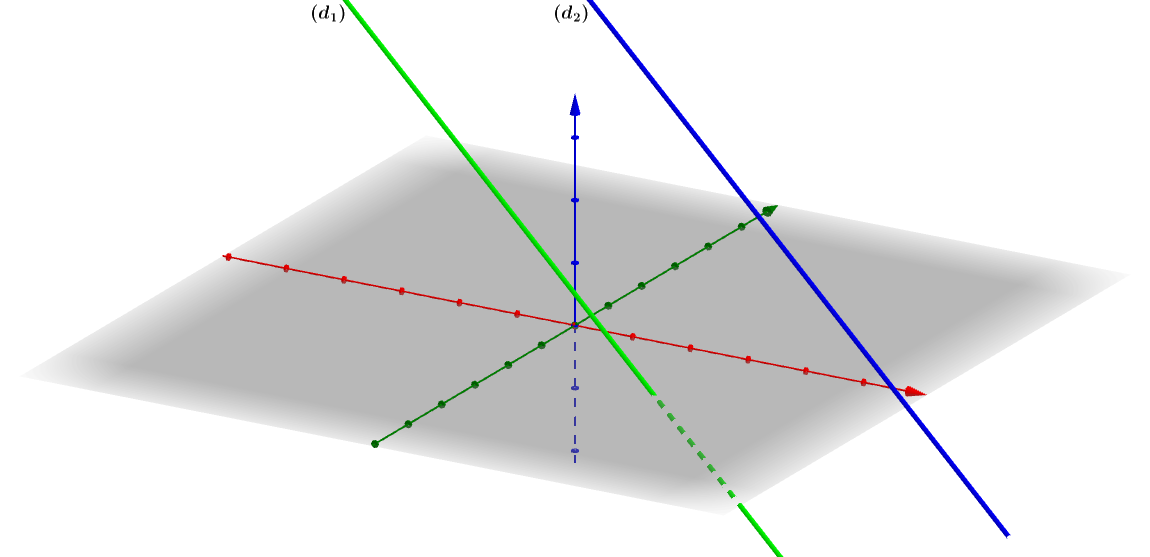
Dễ thấy ![]()
Bước 1 Chọn phương thức tính toán Vector

Bước 2 Khai báo ![]()
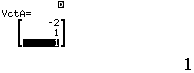
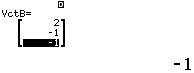
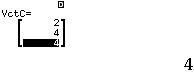
Bước 3 Tính tích có hướng ![]()
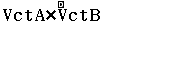
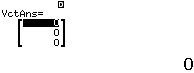
Suy ra ![]() và
và ![]() chỉ có thể trùng nhau hoặc song song
chỉ có thể trùng nhau hoặc song song
Bước 4 Tính tích có hướng ![]()
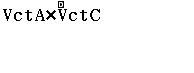
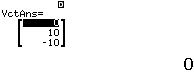
Vậy ![]() song song
song song ![]()
Xét vị trí tương đối của đường thẳng 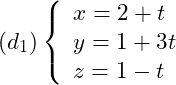 và đường thẳng
và đường thẳng 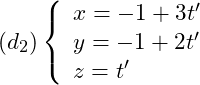
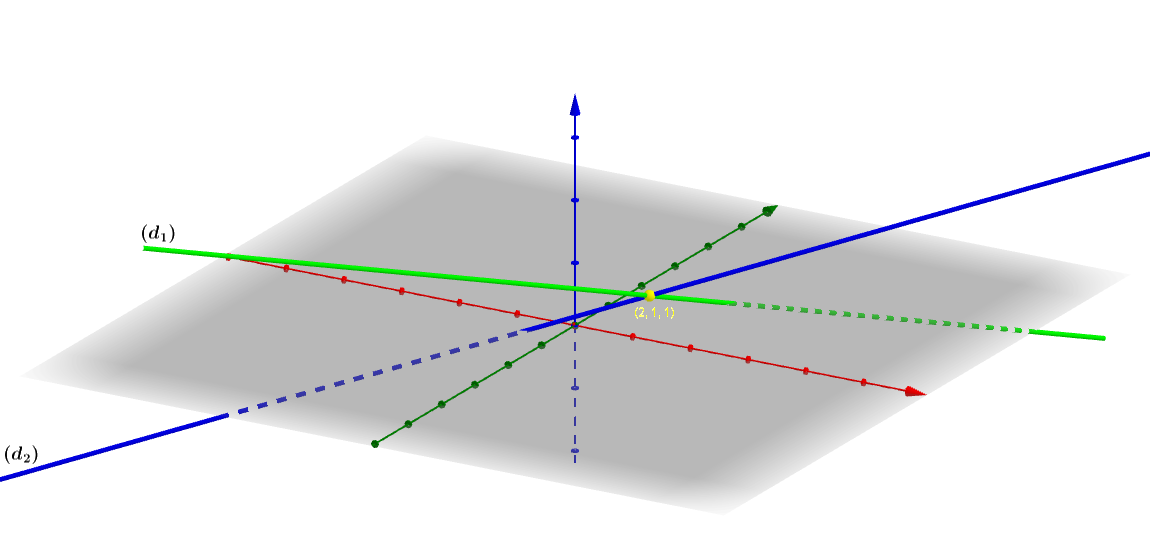
Dễ thấy ![]()
Bước 1 Chọn phương thức tính toán Vector

Bước 2 Khai báo ![]()
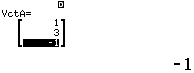
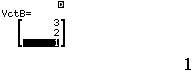
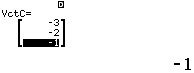
Bước 3 Tính tích có hướng ![]()
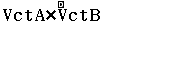
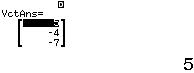
Suy ra ![]() và
và ![]() chỉ có thể cắt nhau hoặc chéo nhau
chỉ có thể cắt nhau hoặc chéo nhau
Bước 4 Tính tích hỗn hợp ![]()
Vì ![]() hiện tại là
hiện tại là ![]() nên chúng ta sẽ nhập
nên chúng ta sẽ nhập ![]()


Vậy ![]() cắt
cắt ![]()
Xét vị trí tương đối của đường thẳng 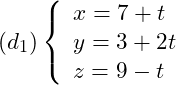 và đường thẳng
và đường thẳng 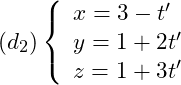
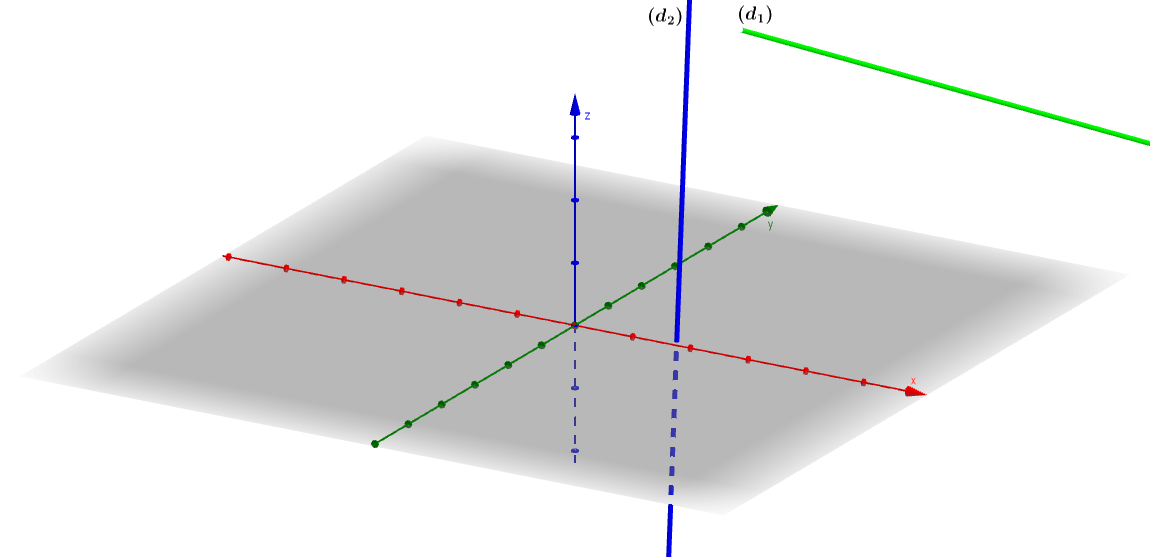
Dễ thấy ![]()
Bước 1 Chọn phương thức tính toán Vector

Bước 2 Khai báo ![]()
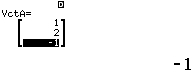
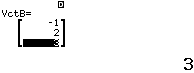
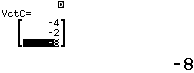
Bước 3 Tính tích có hướng ![]()
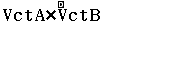
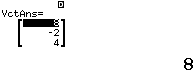
Suy ra ![]() và
và ![]() chỉ có thể cắt nhau hoặc chéo nhau
chỉ có thể cắt nhau hoặc chéo nhau
Bước 4 Tính tích hỗ hợp ![]()


Vậy ![]() chéo
chéo ![]()
