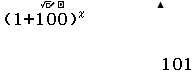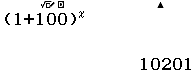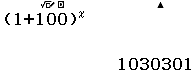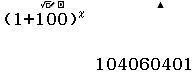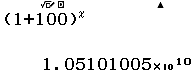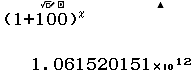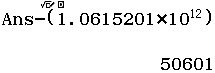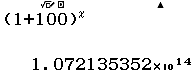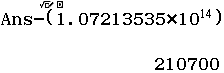Tam giác Pascal là một mảng tam giác của các hệ số nhị thức
Người ta thường sử dụng tam giác này để khai triển các hằng đẳng thức $(x+y)^2$, $(x-y)^2$, $(x+y)^3$, $(x-y)^3$ và tổng quát là khai triển $(x \pm y)^n$
Có nhiều phương pháp để lập tam giác Pascal, hôm nay mình sẽ giới thiệu đến các bạn hai phương pháp mà mình thường sử dụng
1 Dựa vào kiến thức Toán học
Bước 1 Dòng thứ nhất viết một số $1$
Bước 2 Dòng thứ nhì viết hai số $1$
Bước 3 Dòng thứ ba
- Bước 3.1 Số đầu tiên và số cuối cùng viết số $1$

- Bước 3.2 Số ở giữa bằng tổng của hai số ở hàng thứ nhì

Bước 4 Thực hiện tương tự Bước 3 để hoàn thành các dòng tiếp theo

- Số đầu tiên và số cuối cùng của một dòng luôn là số $1$
- Dòng thứ $n$ có $n$ số hạng
- Dòng thứ $n$ tương ứng với bậc $n-1$
2 Dựa vào kiến thức máy tính CASIO fx-580VN X
Ưu điểm lớn nhất của phương pháp này là bạn có thể lập được một dòng bất kì của tam giác, không phụ thuộc vào dòng phía trên
Bước 1 Nhập biểu thức $(1+100)^x$
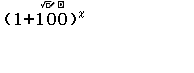
Bước 2 Nhấn phím CALC
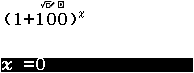
Bước 3 Nhập $0$
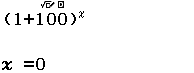
Bước 4 Nhấn phím $=$
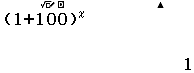
Bước 5 Thực hiện lại Bước 2, Bước 3, Bước 4 với $1, 2, 3, 4, 5, 6, 7$
Bước 6 Vì $x=5, 6, 7$ cho kết quả tính toán tràn màn hình nên chúng ta cần xử lí lại
Suy ra $(1+100)^5=10510100501$
Suy ra $(1+100)^6=1061520150601$
Vì chữ số ngay bên trái dấu $\times$ là chữ số $1$ nên ta phải bỏ ở một vị trí khác. Ở đây mình sẽ bỏ đi chữ số ngay bên trái chữ số này tức chữ số $5$
Suy ra $(1+100)^7=107213535210701$
- Màn hình hiển thị $210700$ nhưng mình lại suy ra $210701$ là vì giá trị $(1+100)^7$ đã tiệm cận khả năng nhớ của máy tính nên nó không còn chính xác
- Giá trị tiệm cận là những giá trị có dạng $a \times 10^{14}$ với $a \in R^*$
- Khi xử lí kết quả tính toán tràn màn hình là nếu chữ số cuối cùng là chữ số $0$ thì chúng ta nên kiểm tra lại
Bước 7 Hoàn thành tam giác Pascal
- Thêm chữ số $0$ vào đầu mỗi kết quả tính toán để tam giác cân đối, tránh sai sót khi sử dụng
- Tách mỗi kết quả tính toán thành từng đôi theo chiều từ phải sang trái

Do hạn chế của máy tính CASIO fx-580VN X nên chúng ta chỉ có thể lập được tám dòng tức lập được bảy bậc
Nếu muốn lập đến bậc cao hơn thì bạn có thể lập thủ công bằng cách sử dụng các kiến thức Toán học
Cao thì cao nhưng cũng chỉ từ bậc mười trở xuống, nếu cao hơn thì nên sử dụng công thức nhị thức Newton
$(a+b)^{n}=C_{n}^{0} a^{n}+C_{n}^{1} a^{n-1} b+\ldots+C_{n}^{k} a^{n-k} b^{k}+\ldots+C_{n}^{n-1} a b^{n-1}+C_{n}^{n} b^{n}$
3 Ứng dụng khai triển biểu thức
Vì mục đích chính là hướng dẫn cho các bạn biết cách ứng dụng tam giác Pascal vào việc khai triển nhị thức, xa hơn là đa thức, phân thức nên các ví dụ minh họa mà mình lựa chọn rất đơn giản
Khai triển $(x+y)^2$
Bước 1 Xác định hệ số của các hạng tử và dấu của chúng
- Xem dòng thứ ba của tam giác Pascal
- Dấu của các hạng tử là dấu $+$
$+1+2+1$
Bước 2 Biểu diễn $x$, tương ứng với mỗi hạng tử bậc của $x$ sẽ giảm dần từ $2$ đến $0$
$+1x^2+2x^1+1x^0$
Bước 3 Biểu diễn $y$, tương ứng với mỗi hạng tử bậc của $y$ sẽ tăng dần từ $0$ đến $2$
$+1x^2y^o+2x^1y^1+1x^0y^2$
Bước 4 Rút gọn biểu thức
$x^2+2xy+y^2$
Vậy $(x+y)^2=x^2+2xy+y^2$
Khai triển $(x-y)^3$
Bước 1 Xác định hệ số của các hạng tử và dấu của chúng
- Xem dòng thứ tư của tam giác Pascal
- Dấu của các hạng tử là dấu $+$ và $-$ đan xen (dấu của hạng tử đầu tiên là dấu $+$)
$+1-3+3-1$
Bước 2 Biểu diễn $x$, tương ứng với mỗi hạng tử bậc của $x$ sẽ giảm dần từ $3$ đến $0$
$+1x^3-3x^2+3x^1-1x^0$
Bước 3 Biểu diễn $y$, tương ứng với mỗi hạng tử bậc của $y$ sẽ tăng dần từ $0$ đến $3$
$+1x^3y^0-3x^2y^1+3x^1y^2-1x^0y^3$
Bước 4 Rút gọn biểu thức
$x^3-3x^2y+3xy^2-y^3$
Vậy $(x-y)^3=x^3-3x^2y+3xy^2-y^3$
Khai triển $(2x+3y)^2$
Bước 1 Xác định hệ số của các hạng tử và dấu của chúng
- Xem dòng thứ ba của tam giác Pascal
- Dấu của các hạng tử là dấu $+$
$+1+2+1$
Bước 2 Biểu diễn $2x$, tương ứng với mỗi hạng tử bậc của $2x$ sẽ giảm dần từ $2$ đến $0$
$+1(2x)^2+2(2x)^1+1(2x)^0$
Bước 3 Biểu diễn $3y$, tương ứng với mỗi hạng tử bậc của $3y$ sẽ tăng dần từ $0$ đến $2$
$+1(2x)^2(3y)^0+2(2x)^1(3y)^1+1(2x)^0(3y)^2$
Bước 4 Rút gọn biểu thức
$4x^2+12xy+9y^2$
Vậy $(2x+3y)^2=4x^2+12xy+9y^2$
Khai triển $\left(\dfrac{2}{x}-\dfrac{3}{y}\right)^3$
Bước 1 Xác định hệ số của các hạng tử và dấu của chúng
- Xem dòng thứ tư của tam giác Pascal
- Dấu của các hạng tử là dấu $+$ và $-$ đen xen (dấu của hạng tử đầu tiên là dấu $+$)
$+1-3+3-1$
Bước 2 Biểu diễn $\dfrac{2}{x}$, tương ứng với mỗi hạng tử bậc của $\dfrac{2}{x}$ sẽ giảm dần từ $3$ đến $0$
$+1\left(\dfrac{2}{x}\right)^3-3\left(\dfrac{2}{x}\right)^2+3\left(\dfrac{2}{x}\right)^1-1\left(\dfrac{2}{x}\right)^0$
Bước 3 Biểu diễn $\dfrac{3}{y}$, tương ứng với mỗi hạng tử bậc của $\dfrac{3}{y}$ sẽ tăng dần từ $0$ đến $3$
$+1\left(\dfrac{2}{x}\right)^3\left(\dfrac{3}{y}\right)^0-3\left(\dfrac{2}{x}\right)^2\left(\dfrac{3}{y}\right)^1+3\left(\dfrac{2}{x}\right)^1\left(\dfrac{3}{y}\right)^2-1\left(\dfrac{2}{x}\right)^0\left(\dfrac{3}{y}\right)^3$
Bước 4 Rút gọn biểu thức
$\dfrac{8}{x^3}-\dfrac{36}{x^2y}+\dfrac{54}{xy^2}-\dfrac{27}{y^3}$
Vậy $\left(\dfrac{2}{x}-\dfrac{3}{y}\right)^3=\dfrac{8}{x^3}-\dfrac{36}{x^2y}+\dfrac{54}{xy^2}-\dfrac{27}{y^3}$
Khai triển $(x+y+z)^2$
Dễ thấy $(x+y+z)^2=[(x+y)+z]^2$
Bước 1 Xác định hệ số của các hạng tử và dấu của chúng
- Xem dòng thứ ba của tam giác Pascal
- Dấu của các hạng tử là dấu $+$
$+1+2+1$
Bước 2 Biểu diễn $(x+y)$, tương ứng với mỗi hạng tử bậc của $(x+y)$ sẽ giảm dần từ $2$ đến $0$
$+1(x+y)^2+2(x+y)^1+1(x+y)^0$
Bước 3 Biểu diễn $z$, tương ứng với mỗi hạng tử bậc của $z$ sẽ tăng dần từ $0$ đến $2$
$+1(x+y)^2z^o+2(x+y)^1z^1+1(x+y)^0z^2$
Vì $(x+y)^2=x^2+2xy+y^2$ nên $+1(x^2+2xy+y^2)z^o$ $+$ $2(x+y)^1z^1$ $+$ $1(x+y)^0z^2$
Bước 4 Rút gọn biểu thức
$x^2+2xy+y^2+2xz+2yz+z^2$
Vậy $(x+y+z)^2=x^2+2xy+y^2+2xz+2yz+z^2$