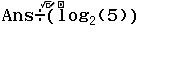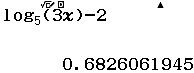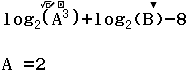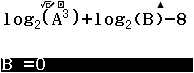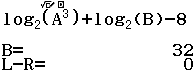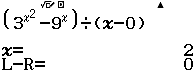Giải đề thi môn Toán Kỳ thi THPT Năm 2021 bằng máy tính CASIO fx-580VN X
Đề thi có tổng cộng 50 câu nhưng mình chỉ hướng dẫn những câu có thể ứng dụng máy tính CASIO fx-580VN X. Những câu còn lại thì mình không hướng dẫn vì đã có rất nhiều người hướng dẫn rồi
Có nhiều câu rất dễ, chỉ cần nhìn vào là có thể chọn ngay đáp án. Tuy nhiên mình vẫn quyết định hướng dẫn chi tiết cho các bạn
Cũng câu này nhưng nếu cho phức tạp hơn thì chắc chắn bạn không thể nhìn ra ngay được. Khi đó nếu biết sử dụng máy tính CASIO fx-580VN X sẽ là một lợi thế lớn
- Phần lớn các chỉ dẫn trong bài viết này đều được thực hiện trong phương thức tính toán Calculate
- Mã đề thi mà mình lựa chọn là 102
1 Đối tượng hướng đến
Bài viết này hướng đến nhiều đối tượng khác nhau nhưng chủ yếu hướng đến
- Học sinh lớp 12 chưa tham dự Kỳ thi Trung học Phổ thông
- Học sinh lớp 11 chuẩn bị lên lớp 12
- Những bạn yêu thích thủ thuật máy tính CASIO fx-580VN X
2 Các câu có thể giải được bằng máy tính CASIO fx-580VN X
Tất cả các thủ thuật được sử dụng trong bài viết này đều được mình hướng dẫn chi tiết trong Series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi Trung học Phổ thông Quốc gia
Trên khoảng ![]() đạo hàm của hàm số
đạo hàm của hàm số 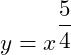 là
là
A. 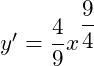
B. 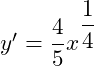
C. 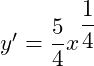
D. 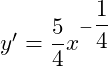
Giả sử chúng ta đã thiết lập sử dụng hai hàm và đã chọn phương thức tính toán Table
Bước 1 Nhập hàm f(x)
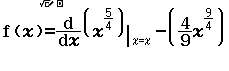
Bước 2 Nhập hàm g(x)
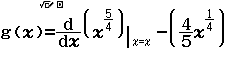
Bước 3 Nhập ![]()
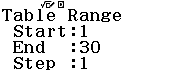
Bước 4

Quan sát bảng giá trị tìm được ta thấy không hàm nào cho giá trị bằng ![]() hoặc tiệm cận
hoặc tiệm cận ![]() nên chúng ta sẽ kiểm tra với phương án C và phương án D
nên chúng ta sẽ kiểm tra với phương án C và phương án D
Bước 5 Nhập lại hàm f(x)
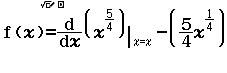
Bước 6 Nhập lại hàm g(x)
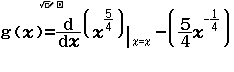
Bước 7 Nhập ![]()

Bước 8

Quan sát bảng trị tìm được ta thấy các giá trị của f(x) đều bằng ![]() hoặc tiệm cận
hoặc tiệm cận ![]()
Số tiệm cận ![]() là số có dạng
là số có dạng ![]() với
với ![]()
Vậy phương án C là đáp án
Tập xác định của hàm số ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã chọn phương thức tính toán Table
Bước 1 Nhập hàm f(x)
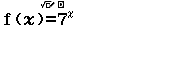
Bước 2 Nhập ![]()
Bước 3
Quan sát bảng giá trị tìm ta thấy không một giá trị nào làm cho f(x) bị ERROR nên tập xác định của hàm số đã cho là R
Vậy phương án D là đáp án
Cho hàm số ![]() . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng?
A. ![]()
B. 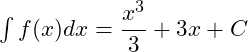
C. ![]()
D. ![]()
Giả sử chúng ta đã thiết lập sử dụng hai hàm và đã chọn phương thức tính toán Table
Bước 1 Nhập hàm f(x)
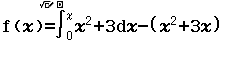
Bước 2 Nhập hàm g(x)
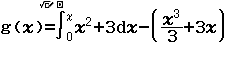
Bước 3 Nhập ![]()

Bước 4
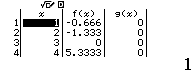
Quan sát bảng trị tìm được của ta thấy g(x) là hàm hằng
g(x) là hàm hằng vì tất cả các giá trị tìm được đều là hằng số và có cùng một giá trị
Vậy phương án B là đáp án
Cho ![]() và
và ![]() , khi đó
, khi đó ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Nhấn phím Ran# => nhấn phím STO => nhấn phím A

Bước 2 Nhập hàm ![]() => nhấn phím =
=> nhấn phím =
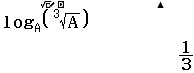
Vậy phương án B là đáp án
Đồ thị của hàm số ![]() cắt trục tung tại điểm có tung độ bằng
cắt trục tung tại điểm có tung độ bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
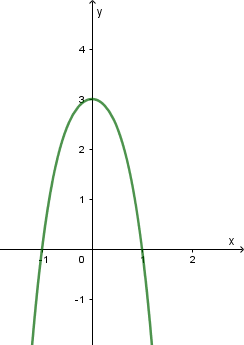
Bước 1 Nhập hàm số ![]() => nhấn phím CALC => nhập
=> nhấn phím CALC => nhập ![]()
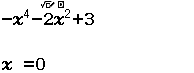
Bước 2 Nhấn phím =
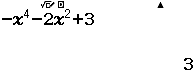
Vậy phương án D là đáp án
Cho hai số phức ![]() và
và ![]() . Số phức
. Số phức ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã chọn phương thức tính toán Complex
Bước 1 Nhập ![]()
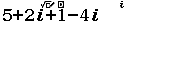
Bước 2 Nhấn phím =
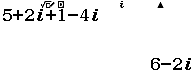
Vậy phương án C là đáp án
Cho hàm số ![]() . Khẳng định nào dưới đây là đúng?
. Khẳng định nào dưới đây là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã thiết lập sử dụng hai hàm và đã chọn phương thức tính toán Table
Bước 1 Nhập hàm f(x)
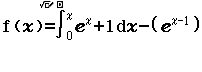
Bước 2 Nhập hàm g(x)
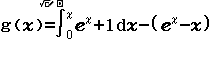
Bước 3 Nhập ![]()

Bước 4

Quan sát bảng giá trị tìm được ta nhận thấy không hàm nào là hàm hằng nên chúng ta sẽ kiểm tra với phương án C và phương án D
Bước 5 Nhập lại hàm f(x)

Bước 6 Nhập lại hàm g(x)

Bước 7 Nhập ![]()

Bước 8
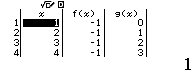
Quan sát bảng giá trị tìm được ta nhận thấy f(x) là hàm hằng
Vậy phương án C là đáp án
Tiệm cận đứng của đồ thị hàm số ![]() là đường thẳng có phương trình
là đường thẳng có phương trình
A. ![]()
B. ![]()
C. ![]()
D. ![]()
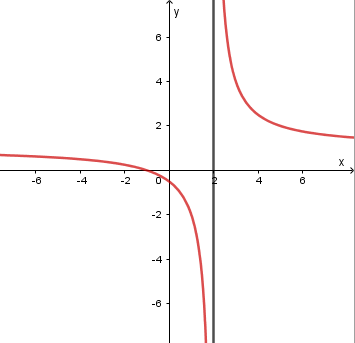
Bước 1 Nhập hàm ![]()

Bước 2 Nhấn phím CALC => nhập ![]()
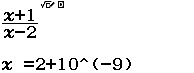
Bước 3 Nhấn phím =
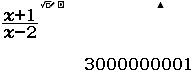
Vì ![]() nên
nên ![]() là đường tiệm cận đứng của đồ thị hàm số
là đường tiệm cận đứng của đồ thị hàm số
Vậy phương án C là đáp án
Phần thực của số phức ![]() bằng
bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã chọn phương thức tính toán Complex
Bước 1 Nhấn phím OPTN => nhấn phím 3

Bước 2 Nhập số phức ![]() => nhấn phím =
=> nhấn phím =
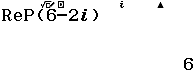
Vậy phương án C là đáp án
Tập nghiệm của bất phương trình ![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Giải phương trình ![]()

Bước 2 Nhấn phím ![]() => nhập
=> nhập ![]() => nhấn phím =
=> nhấn phím =
Suy ra nghiệm tìm được ở Bước 1 chính là ![]()
Bước 3 Lập bảng xét dấu
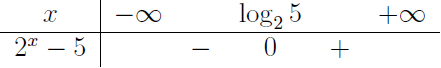
Lấy một giá trị bất kì thuộc khoảng ![]() thay vào hàm
thay vào hàm ![]() nếu kết quả tìm được là một số dương thì dấu cần tìm là dấu
nếu kết quả tìm được là một số dương thì dấu cần tìm là dấu ![]() và ngược lại
và ngược lại
Vậy phương án A là đáp án
Nghiệm của phương trình ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Nhập hàm ![]()
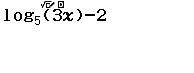
Bước 2
- Nhấn phím CALC
- Nhập thử lần lượt bốn giá trị ở bốn phương án. Phương án nào cho giá trị bằng
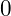 thì đó chính là đáp án
thì đó chính là đáp án
Vậy phương án D là đáp án
- Bạn không nên sử dụng tính năng SOLVE để tìm nghiệm của phương trình
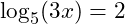 nói riêng hay phương trình Logarit nói chung vì quá trình này mất khá nhiều thời gian
nói riêng hay phương trình Logarit nói chung vì quá trình này mất khá nhiều thời gian - Ngoài sử dụng tính năng CALC bạn cũng có thể sử dụng phương thức tính toán Table
Cho số phức ![]() thỏa mãn
thỏa mãn ![]() . Số phức liên hợp của
. Số phức liên hợp của ![]() là
là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giả sử chúng ta đã chọn phương thức tính toán Complex
Bước 1 Nhấn phím OPTN => nhấn phím 2
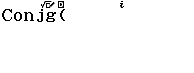
Bước 2 Nhập số phức ![]() => nhấn phím =
=> nhấn phím =
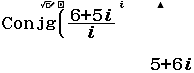
Vậy phương án C là đáp án
Trên đoạn ![]() hàm số
hàm số ![]() đạt giá trị lớn nhất tại điểm
đạt giá trị lớn nhất tại điểm
A. ![]()
B. ![]()
C. ![]()
D. ![]()
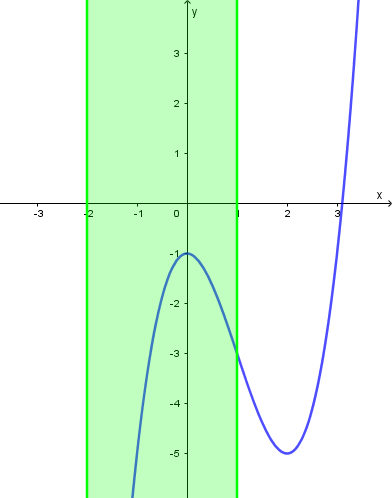
Giả sử chúng ta đã chọn phương thức tính toán Table
Bước 1 Nhập hàm số ![]()
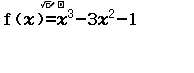
Bước 2 Nhập ![]()
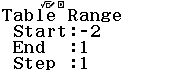
Bước 3 Nhấn phím =
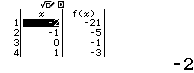
Vậy phương án B là đáp án
Với mọi ![]() thỏa mãn
thỏa mãn ![]() khẳng định nào dưới đây là đúng?
khẳng định nào dưới đây là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Bước 1 Nhập hàm ![]()
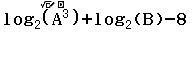
Bước 2 Nhấn phím SOLVE => nhập ![]() => nhấn phím = => nhấn phím =
=> nhấn phím = => nhấn phím =
Suy ra ![]() hay
hay ![]()
Bạn có thể nhập ![]() một số khác, mình nhập
một số khác, mình nhập ![]() là để
là để ![]() có giá trị là một số tự nhiên (để dễ xử lí)
có giá trị là một số tự nhiên (để dễ xử lí)
Vậy phương án B là đáp án
Có bao nhiêu số nguyên ![]() thỏa mãn
thỏa mãn ![]()
A. ![]()
B. Vô số
C. ![]()
D. ![]()
Bước 1 Sử dụng tính năng SOLVE giải phương trình ![]()
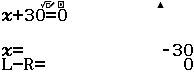
Suy ra tập xác định của bất phương trình đã cho là ![]()
Bước 2 Sử dụng tính năng SOLVE giải phương trình ![]()
Suy ra tập nghiệm của phương trình ![]() là
là ![]()
Bước 3 Sử dụng tính năng SOLVE giải phương trình ![]()

Suy ra tập nghiệm của phương trình ![]() là
là ![]()
Bước 4 Lập bảng xét dấu

Suy ra tập nghiệm của bất phương trình đã cho là ![]()

Vậy phương án C là đáp án