Tìm hạng của ma trận vuông bằng CASIO fx 880 BTG

19/10/202201/08/2023Nhut Nguyen Minh

Xin chào tất cả các bạn

Hôm nay, mình sẽ hướng dẫn các bạn tìm hạng của ma trận vuông bằng máy tính cầm tay CASIO fx 880 BTG

Mục lục nội dung

1 Kiến thức Toán học

Hạng của ma trận là cấp cao nhất của các định thức con khác 0

Nói cách khác hạng của ma trận A bằng r nếu tồn tại ít nhất một định thức con cấp r khác 0 và mọi định thức cấp con cao hơn r đều bằng 0

Hạng của ma trận A được kí hiệu là $r_A$

2 Các bước thực hiện

Giả sử mình cần tìm hạng của ma trận vuông A cấp n thì thực tuần tự theo các bước bên dưới

Bước 1 tính định thức của ma trận A

Nếu định thức của ma trận A khác 0 thì hạng của ma trận A bằng n
Nếu định thức của ma trận A bằng 0 thì hạng của ma trận A nhỏ hơn hoặc bằng n-1

Bước 2 tính các định thức của các ma trận con cấp n-1 của ma trận A

Nếu tồn tại định thức của ma trận con cấp n-1 khác 0 thì hạng của ma trận A bằng n-1
Nếu tất cả các định thức của ma trận con cấp n-1 đều bằng 0 thì hạng của ma trận A nhỏ hơn hoặc bằng n-2

Bước 3 …

Xem thêm Tính định thức Det của ma trận bằng CASIO fx 880 BTG

3 Ví dụ minh họa

Chẳng hạn mình cần tìm hạng của ma trận $A=\left[\begin{matrix} 1 & 2 & 6 & 7 \\ 0 & 2 & 5 & 5 \\ 6 & 0 & 8 & 6 \\ 7 & 6 & 7 & 7 \end{matrix}\right]$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 mở ứng dụng ma trận Matrix

Nhấn phím HOME => sử dụng các phím con trỏ chọn Matrix => nhấn phím OK

Bước 2 gán ma trận vào biến nhớ ma trận MatA

Bước 2.1 nhấn phím TOOLS => chọn MatA => nhấn phím OK

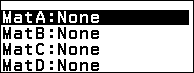
Bước 2.2

Nhấn phím OK => chọn 4 Rows => nhấn phím OK

Nhấn phím OK => chọn 4 Columns => nhấn phím OK

Nhấn phím OK

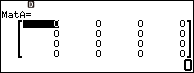
Bước 2.3 lần lượt nhất các phím …

… để nhập các phần tử của ma trận

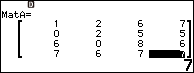
Bước 2.4 nhấn phím EXE

Bước 3 gọi lệnh Determinant

Nhấn phím CATALOG => chọn Matrix => nhấn phím OK => chọn Matrix Calc => nhấn phím OK => chọn Determinant => nhấn phím OK

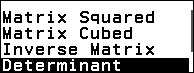
Bước 4 gọi ma trận MatA

Nhấn phím CATALOG => chọn Matrix => nhấn phím OK => chọn MatA => nhấn phím OK

Bước 5 nhấn phím EXE

Vì định thức của ma trận A bằng $-268 \neq 0$ nên hạng của ma trận A bằng 4

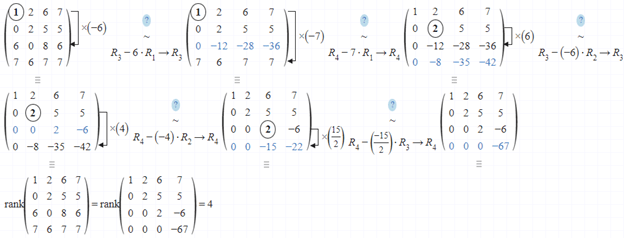
Chẳng hạn 2 mình cần tìm hạng của ma trận $B=\left[\begin{matrix} 9 & 2 & 2 & 2 \\ 4 & 0 & 7 & 1 \\ 8 & 1 & 4 & 0 \\ 35 & 40 & 45 & 159 \end{matrix}\right]$ thì thực hiện tuần tự theo các bước bên dưới

Thực hiện tương tự Bước 1 đến Bước 5 để tính định thức của ma trận B

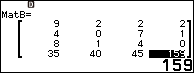
Vì định thức của ma trận B bằng 0 nên hạng của ma trận B nhỏ hơn hoặc bằng 3

Bây giờ chúng ta sẽ có gắng tìm một ma trận con cấp 3 có định thức khác 0, nếu tìm được thì kết luận hạng của ma trận B bằng 3

Ở đây mình sẽ chọn ma trận $\left[\begin{matrix}9&2&2\\4&0&7\\8&1&4\end{matrix}\right]$

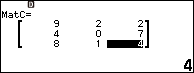
Vậy ma trận B có hạng là 3

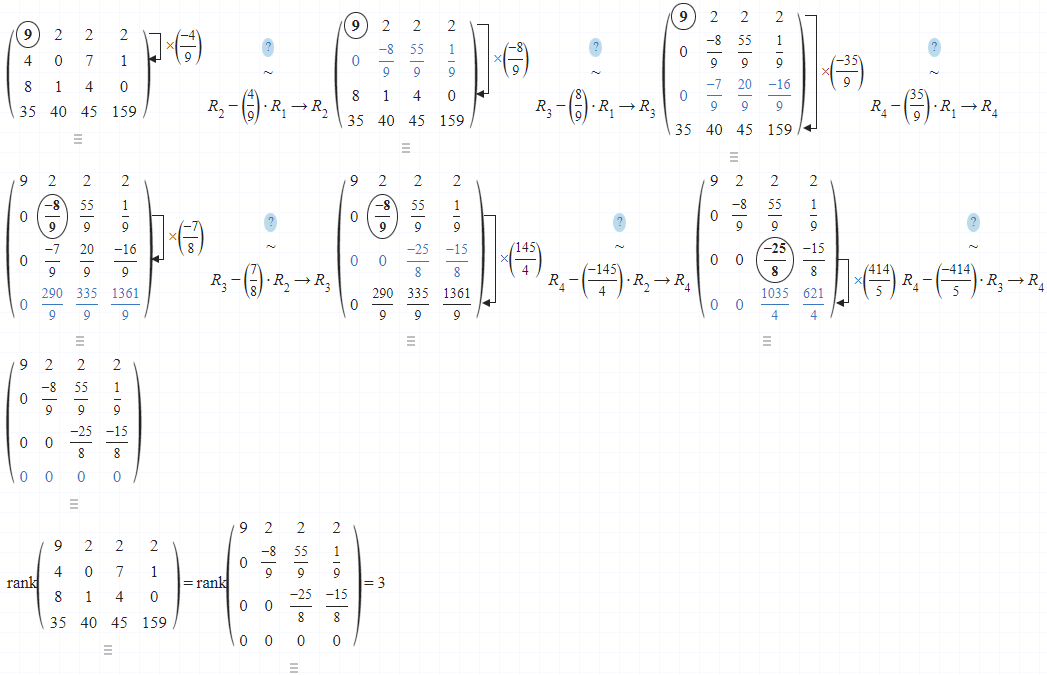
Nếu ma trận con cấp 3 mà bạn vừa chọn có định thức bằng 0 thì vẫn chưa thể kết luận hạng của ma trận B là nhỏ hơn hoặc bằng 2
Chúng ta chỉ có thể kết luận hạng của ma trận B nhỏ hơn hoặc bằng 2 khi tất cả các định thức con cấp 3 đều bằng 0

4 Lời kết

Máy tính cầm tay CASIO fx 880 BTG có thể tìm được hạng của ma trận vuông một cách nhanh chóng nhưng cũng có thể lâu lắc

Nhanh chóng hay lâu lắc phụ thuộc vào việc chọn các định thức con cấp n-1

Ngoài ra nếu ma trận cần tìm hạng là ma trận vuông cấp 5 thì việc áp dụng thủ thuật này tốn khá nhiều thời gian

Lúc bấy giờ bạn hãy sử dụng phép khử Gaussian bạn nhá

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

1 Kiến thức Toán học

2 Các bước thực hiện

3 Ví dụ minh họa

4 Lời kết

Trả lời Hủy