Cách tính tích hỗn hợp / tích hỗn tạp bằng CASIO fx 880 BTG

12/10/202229/08/2023Nhut Nguyen Minh

Xin chào tất cả các bạn

Trong các phép tính véc tơ, ngoài tích vô hướng, tích có hướng như các bạn đã biết còn có một loại tích nữa cũng có nhiều ứng dụng trong học tập kiểm tra và thi cử

Phép tính tích mà mình muốn nhắc ở đây chính là tích hỗn hợp (một số tài liệu còn gọi là tích hỗn tạp)

Việc tính tích hỗn hợp bằng kiến thức Toán học tốn khá nhiều công sức và thời gian

Vậy nên thay vì phải vất vả tính tích hỗn hợp bằng kiến thức Toán học, chúng ta nên bằng máy tính cầm tay CASIO fx 880 BTG các bạn nhá

https://www.youtube.com/watch?v=P9rxdUwEX_Q

Mục lục nội dung

1 Sơ lược về tích hỗn hợp

Trong không gian $Oxyz$ cho ba véc tơ $\vec{a}, \vec{b}, \vec{c}$

Lúc bấy giờ nếu lấy tích vô hướng của tích có hướng $[\vec{a}, \vec{b}]$ và $\vec{c}$ sẽ thu được tích hỗn hợp

$[\vec{a}, \vec{b}] \cdot \vec{c}$

Tích hỗn hợp của ba véc tơ là một số thực

Tích hỗn hợp thường được sử dụng để tính thể tích của hình tứ diện, hình hộp

2 Các bước thực hiện

Bước 1 mở ứng dụng véc tơ

Bước 2 gán véc tơ thứ nhất vào biến nhớ véc tơ VctA

Bước 3 gán véc tơ thứ nhì vào biến nhớ véc tơ VctB

Bước 4 gán véc tơ thứ ba vào biến nhớ véc tơ VctC

Bước 5 nhập $(VctA \times VctB) \cdot VctC$

Bước 6 nhấn phím EXE

3 Ví dụ minh họa

Chẳng hạn mình cần tính tích hỗn hợp của $\vec{a}=(3, 2, 7), \vec{b}=(2, 7, 6), \vec{c}=(6, 4, 0)$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 mở ứng dụng véc tơ

Nhấn phím HOME => sử dụng các phím con trỏ chọn Vector => nhấn phím OK

Bước 2 gán véc tơ $\vec{a}=(3, 2, 7)$ vào biến nhớ véc tơ VctA

Bước 2.1 nhấn phím TOOLS => chọn VctA => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

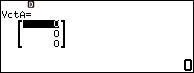
Bước 2.2 nhập 3 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập 7 => nhấn phím EXE

Bước 2.3 nhấn phím EXE

Bước 3 gán véc tơ $\vec{b}=(2, 7, 6)$ vào biến nhớ véc tơ VctB

Bước 3.1 nhấn phím TOOLS => chọn VctB => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

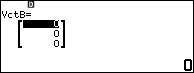
Bước 3.2 nhập 2 => nhấn phím EXE => nhập 7 => nhấn phím EXE => nhập 6 => nhấn phím EXE

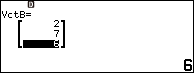
Bước 3.3 nhấn phím EXE

Bước 4 gán véc tơ $\vec{c}=(6, 4, 0)$ vào biến nhớ véc tơ VctC

Bước 4.1 nhấn phím TOOLS => chọn VctC => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

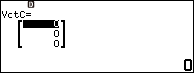
Bước 4.2 nhập 6 => nhấn phím EXE => nhập 4 => nhấn phím EXE => nhập 0 => nhấn phím EXE

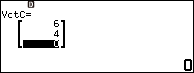
Bước 4.3 nhấn phím EXE

Bước 3 nhập $(VctA \times VctB) \cdot VctC$

Bước 3.1 nhấn phím ( => nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctA => nhấn phím OK

Bước 3.2 nhấn phím $\times$

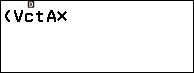
Bước 3.3 nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctB => nhấn phím OK => nhấn phím )

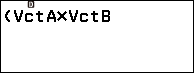
Bước 3.4 nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn Vector Calc => nhấn phím OK => chọn Dot Product => nhấn phím OK

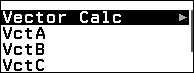
Bước 3.5 nhấn phím CATALOG => chọn Vector => nhấn phím OK => chọn VctC => nhấn phím OK

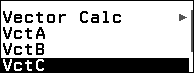
Bước 4 nhấn phím EXE

Vậy tích hỗn hợp của ba véc tơ $\vec{a}=(3, 2, 7), \vec{b}=(2, 7, 6), \vec{c}=(6, 4, 0)$ là $-238$

4 Lời kết

Việc tính tích hỗn hợp của ba véc tơ bằng máy tính cầm tay CASIO fx 880 BTG không có gì khó khăn, phức tạp

Có nhiều bước, nhiều tao tác như vậy là vì bản thân fx 880 BTG đã có nhiều thao tác và mình lại hướng dẫn chi tiết từng thao tác một

Tuy nhiên đó không phải là vấn đề, bạn đọc thì cũng thấy rất nhiều thao tác lập đi, lập lại phải không nào

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

1 Sơ lược về tích hỗn hợp

2 Các bước thực hiện

3 Ví dụ minh họa

4 Lời kết

Trả lời Hủy