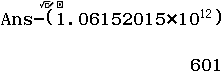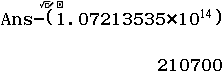Bàn về các thủ thuật máy tính CASIO fx-580VN X

05/08/202105/08/2021Nhut Nguyen Minh

Năm 2017 Bộ Giáo dục và Đào tạo đã thay đổi hình thức thi của môn Toán (TRẮC NGHIỆM) và giữ nguyên đến thời điểm hiện tại

Với hình thức thi này, việc sử dụng hiệu quả máy tính cầm tay nói chung, máy tính CASIO fx-580VN X nói riêng sẽ là một lợi thế lớn

Hiện tại, các thủ thuật máy tính đã được chia sẽ rất nhiều trên Internet cũng như trên https://nhutnguyenminh.com

Một số thủ thuật máy tính tiêu biểu

Xét sự đồng biến, nghịch biến của hàm số
Tìm cực trị của hàm số
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Tìm đường tiệm cận
Khảo sát sự biến thiên của hàm số
…

Trong bài viết chúng ta sẽ cùng nhau bàn về phương pháp sáng tạo, tính chính xác và tính ứng dụng của các thủ thuật máy tính

Mục lục nội dung

1 Phương pháp sáng tạo

Về cơ bản để có thể sáng tạo ra các thủ thuật máy tính chúng ta cần có kiến thức Toán học và kiến thức máy tính

Hai mảng kiến thức trên là tiên quyết, ngoài ra chúng ta còn cần thêm lòng đam mê và đôi khi là một chút may mắn

Thông qua https://nhutnguyenminh.com mình đã chia sẽ với các bạn khá nhiều thủ thuật

Các thủ thuật này một số là do mình sáng tạo, một số là phát triển và số còn lại là biên tập

Viết phương trình đường thẳng (trên mặt phẳng) đi qua hai điểm là một trong các thủ thuật do mình sáng tạo ra

Kiến thức Toán học

Giả sử phương trình đường thẳng cần tìm có dạng $y=ax+b$ và tọa độ của hai điểm đi qua là $(x_1, y_1), (x_2, y_2)$

Khi đó $a, b$ là nghiệm của hệ phương trình $\left \{\begin{array}{l}ax_1+b=y_1\\ ax_2+b=y_2 \end{array} \right.$

Kiến thức máy tính

Sử dụng phương thức tính toán Equation/ Func giải hệ phương trình $\left \{\begin{array}{l}ax_1+b=y_1\\ ax_2+b=y_2 \end{array} \right.$

Ví dụ 1

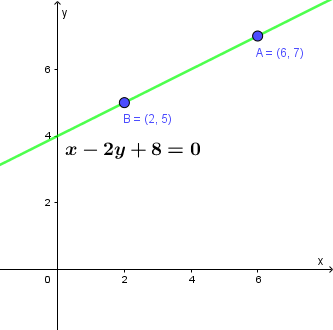
Viết phương trình đường thẳng đi qua hai điểm $A=(6; 7), B=(2; 5)$

Bước 1 Chọn phương thức tính toán Equation/ Func

Bước 2 Chọn Simul Equation

Bước 3 Nhấn phím 2

Bước 4 Nhập các hệ số của hệ phương trình $\left \{ \begin{array}{l}6a+b=7\\ 2a+b=5 \end{array} \right.$

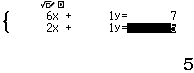
Bước 5 Nhấn phím =

Vậy phương trình đường thẳng cần tìm là $y=\dfrac{1}{2}x+4$

2 Tính chính xác

2.1 Thực trạng

Tính chính xác của phần lớn các thủ thuật máy tính hiện tại chỉ ở mức tương đối

Nói cách khác nó đúng, khả dụng với các trường hợp thường gặp, với các trường hợp đặc biệt có thể không đúng, không khả dụng

Ví dụ 2.1

Viết phương trình đường thẳng đi qua hai điểm $C=(3; 1), D=(3; 4)$

Bước 1 Nhập các hệ số của hệ phương trình $\left \{ \begin{array}{l}3a+b=1\\ 3a+b=4 \end{array} \right.$

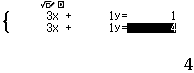
Bước 2 Nhấn phím =

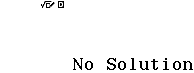
Vậy thủ thuật vừa giới thiệu không khả dụng trong trường hợp này

2.2 Nguyên nhân

Không giống như thuật giải Toán học, thuật giải (thủ thuật) máy tính không có cách nào chứng minh (kiểm tra) với mọi trường hợp

Thông thường để kiểm tra tính đúng đắn, người sáng tạo sẽ kiểm tra với một số trường hợp cụ thể rồi đưa ra kết luận

2.2.1 Chủ quan

Kiến thức Toán học, máy tính còn hạn chế
Sơ suất trong quá trình kiểm tra

2.2.2 Khách quan

Bài toán chống máy tính
Bài toán rơi vào các trường hợp đặc biệt

Ngoài còn một nguyên nhân đặc biệt nữa khả năng tính toán của máy tính

Thủ thuật vừa giới thiệu không khả dụng vì phương trình đường thẳng cần tìm song song với trục tung

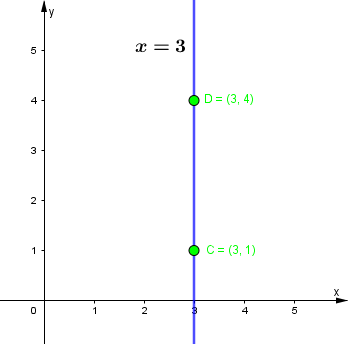
Nguyên nhân sơ suất trong quá trình kiểm tra

Giải pháp bổ sung chú ý nếu phương trình đường thẳng cần tìm trùng hoặc song song với trục tung thì thủ thuật không khả dụng

Viết phương trình đường thẳng đi qua hai điểm

Giả sử phương trình đường thẳng cần tìm có dạng $y=ax+b$ và tọa độ của hai điểm đi qua là $(x_1, y_1), (x_2, y_2)$

Khi đó $a, b$ là nghiệm của hệ phương trình $\left\{\begin{array}{l}ax_1+b=y_1\\ax_2+b=y_2\end{array}\right.$

Viết phương trình đường thẳng đi qua hai điểm

Nếu phương trình đường thẳng cần tìm trùng hoặc song song với trục tung thì thủ thuật không khả dụng

Ví dụ 2.2.1

Xử lí kết quả tính toán tràn màn hình $(1+100)^6$

Vậy $(1+100)^6=106~152~015~601$

Kết luận trên là Sai, chính xác là $1~061~520~150~601$

Nguyên nhân kiến thức Toán học, máy tính còn hạn chế

Chữ số bỏ đi là chữ số $1$ nhưng thật sự là chữ số $0$
Chữ số $0$ là chữ số đầu tiên nên máy tính không hiển thị

Giải pháp nếu vị trí chữ số bỏ đi là chữ số $1$ thì bỏ ở một vị trí khác

Ví dụ 2.2.2

Xử lí kết quả tính toán tràn màn hình $(1+100)^7$

Vậy $(1+100)^7=107~213~535~210~700$

Kết luận trên là Sai, chính xác là $107~213~535~210~701$

Nguyên nhân khả năng tính toán của máy tính

Giải pháp khi chữ số cuối cùng là chữ số $0$ thì cần kiểm tra cẩn thận lại bằng các thủ thuật khác

Xử lí kết quả tính toán tràn màn hình

Giả sử chúng ta có kết quả tính toán $a.bcdefghij \times 10^n$

Bước 1 Nhấn phím $-$

Bước 2

Nếu chữ số $j\neq1$ thì chúng ta sẽ nhập $a.bcdefghi \times 10^n$
Nếu chữ số $j=1$ thì chúng ta sẽ nhập $a.bcdefgh \times 10^n$

Bước 3 Nhấn phím =

Xử lí kết quả tính toán tràn màn hình

Nếu chữ số cuối cùng sau khi xử lí là chữ số $0$ thì chúng ta cần kiểm tra cẩn thận lại
Số mũ tối đa là có thể áp dụng thủ thuật này là $14$
Giá trị $a.bcdefghij \times 10^n$ có $n+1$ chữ số

Ví dụ 2.2.3

Cho $\displaystyle \int_{16}^{55} \dfrac{dx}{x \sqrt{x+9}}=a \ln 2+ b \ln 5+ c \ln 11$ với $a, b, c$ là các số hữu tỉ. Mệnh đề nào dưới đây là đúng

A. $a-b=-c$

B. $a+b=c$

C. $a+b=3c$

D. $a-b=-3c$

Bước 1 Biến đổi sơ cấp $\displaystyle \int_{16}^{55} \dfrac{dx}{x \sqrt{x+9}}=a \ln 2+ b \ln 5+ c \ln 11 \Leftrightarrow e^{^{\displaystyle \int_{16}^{55} \dfrac{dx}{x \sqrt{x+9}}}}=2^a5^b11^c$

Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập tích phân $\displaystyle e^{^{\displaystyle x \int_{16}^{55} \dfrac{dx}{x \sqrt{x+9}}}}$

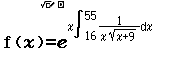
Bước 4 Nhập $Start=1, End=45, Step=1$

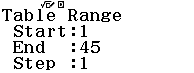
Bước 5 Tìm và ghi nhớ những f(x) có giá trị là số hữu tỉ

Quan sát bảng giá trị chúng ta nhận thấy $f(3)=1.818181818=\dfrac{20}{11}$

Bước 6 Chọn phương thức tính toán Calculate

Bước 7 Sử dụng tính năng FACT phân tích tử số và mẫu số thành thừa số nguyên tố

Suy ra $\dfrac{20}{11}=\dfrac{2^25^1}{11^1}$

Bước 8 Biến đổi sơ cấp rồi suy ra các giá trị $a_{1}, a_{2}, \ldots, a_{n}$

Vì $f(3)=\dfrac{20}{11}=\dfrac{2^25^1}{11^1}=2^25^111^{-1}$ nên $a=\dfrac{2}{3}, b=\dfrac{1}{3}, c=\dfrac{-1}{3}$

Vậy phương án A là đáp án

Ví dụ 2.2.4

Cho $\displaystyle \int_{5}^{21} \dfrac{dx}{x \sqrt{x+4}}=a \ln 3+b \ln 5+c \ln 7$ với $a, b, c$ là các số hữu tỉ. Mệnh đề nào dưới đây đúng

A. $a+b=-2 c$

B. $a+b=c$

C. $a-b=-c$

D. $a-b=-2 c$

Ví dụ 2.2.4 hoàn toàn tương tự Ví dụ 2.2.3 nhưng không áp dụng được thủ thuật Tính tích phân bằng máy tính Casio fx-580VN X

Nguyên nhân Ví dụ 2.2.4 chống máy tính, Ví dụ 2.2.3 áp dụng được chỉ là may mắn

Giải pháp sử dụng kiến thức Toán học

Các thủ thuật nâng cao thường gặp vấn đề này, đó là nguyên nhân mình ít chia sẽ chúng với các bạn

2.3 Giải pháp

2.3.1 Đối với người sáng tạo

Kiểm tra với nhiều trường hợp
Kiểm tra tất cả các trường hợp đặc biệt

Thủ thuật Viết phương trình đường thẳng đi qua hai điểm có 4 trường hợp đặc biệt là song song với trục tung (trục hoành), trùng với trục tung (trục hoành)

2.3.2 Đối với người sử dụng

Đọc kĩ thủ thuật, đặc biệt là các chú ý
Thực hành đầy đủ các ví dụ
Áp dụng giải các bài toán tương tự, ưu tiên đề thi chính thức, đề thi tham khảo

Làm như trên có nhiều lợi ít, tiêu biểu nhất là nhớ được thủ thuật, vận dụng thành thạo và nếu thủ thuật có vấn đề thì nhiều khả năng bạn sẽ phát hiện

3 Tính ứng dụng

Các tính năng, các thủ thuật cơ bản sẽ có tính ứng dụng cao hơn các tính năng, các thủ thuật nâng cao

Tính năng CALC và thủ thuật SOLVE được sử dụng rất nhiều
Tính năng tìm cực trị của hàm số bậc ba, thủ thuật Tính tích phân bằng máy tính Casio fx-580VN X được sử dụng ít hơn

Điều quan trọng là biết khi nào sử dụng thủ thuật máy tính, khi nào sử dụng kiến thức Toán học và khi nào sử dụng cả hai

Chi tiết và đầy đủ bạn có thể xem tại đây