Tính định thức của ma trận cấp 5 bằng máy tính CASIO fx-580VN X

06/08/202103/03/2023Nhut Nguyen Minh

Phương thức tính toán Matrix cho phép chúng ta thực hiện các “phép toán” cơ bản với ma trận như cộng, nhân, ma trận bình phương, ma trận lập phương, định thức, ma trận chuyển vị, ma trận đơn vị, ma trận nghịch đảo, …

Tuy nhiên phương thức này chỉ hỗ trợ tối đa đến ma trận cấp $4 \times 4$ . Muốn thực hiện với các ma trận có cấp cao hơn, chúng ta cần thực hiện thủ công ở một số bước

Trong phạm vi của bài viết này, mình sẽ hướng dẫn các bạn tính định thức của ma trận cấp 5 bằng máy tính CASIO fx-580VN X

Ngoài ra mình cũng hướng dẫn thêm hai phương pháp khác là sử dụng ứng dụng Photomath và dịch vụ WolframAlpha

Tính $A=\left|\begin{array}{lllll} 5 & 4 & 5 & 8 & 4 \\ 6 & 5 & 3 & 2 & 5 \\ 3 & 9 & 8 & 8 & 0 \\ 9 & 3 & 0 & 9 & 5 \\ 5 & 3 & 3 & 0 & 9 \end{array}\right|$

Mục lục nội dung

1 Dựa vào máy tính CASIO fx-580VN X

Chuẩn bị kiến thức

Ở đây mình chọn dòng thứ ba vì dòng này có một số 0, dòng nào có nhiều số 0 thì chúng ta sẽ ưu tiên chọn dòng đó

Dễ thấy $|A|=3|A_1|-9|A_2|+8|A_3|-8|A_4|+0|A_5|$ với $A_1$ , $A_2$ , $A_3$ , $A_4$ lần lượt

$\left|\begin{array}{llll} 4 & 5 & 8 & 4 \\ 5 & 3 & 2 & 5 \\ 3 & 0 & 9 & 5 \\ 3 & 3 & 0 & 9 \end{array}\right|, \left|\begin{array}{llll} 5 & 5 & 8 & 4 \\ 6 & 3 & 2 & 5 \\ 9 & 0 & 9 & 5 \\ 5 & 3 & 0 & 9 \end{array}\right|, \left|\begin{array}{llll} 5 & 4 & 8 & 4 \\ 6 & 5 & 2 & 5 \\ 9 & 3 & 9 & 5 \\ 5 & 3 & 0 & 9 \end{array}\right|, \left|\begin{array}{llll} 5 & 4 & 5 & 4 \\ 6 & 5 & 3 & 5 \\ 9 & 3 & 0 & 5 \\ 5 & 3 & 3 & 9 \end{array}\right|$

Ma trận $A_5$ thì không cần định nghĩa vì cho dù giá trị $|A_5|$ bằng bao nhiêu thì vẫn không ảnh hướng đến giá trị của $|A|$

Bước 1 Định nghĩa ma trận $MatA=A_1$

Bước 2 Định nghĩa ma trận $MatB=A_2$

Bước 3 Định nghĩa ma trận $MatC=A_3$

Bước 4 Định nghĩa ma trận $MatD=A_4$

Bước 5 Tính $3|A_1|-9|A_2|+8|A_3|-8|A_4|$

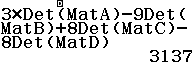
Vậy $|A|=3137$

Giả sử cần phải định nghĩa $A_5$ thì chúng ta sẽ thực hiện

Bước 1 Định nghĩa $A_1, A_2, A_3$ và $A_4$

Bước 2 Tính giá trị biểu thức $A'$ biết $A'=3|A_1|-9|A_2|+8|A_3|-8|A_4|$

Bước 3 Định nghĩa $A_5$ cho biến nhớ ma trận $MatA$

Bước 4 Tính $|A|$ biết $|A|=A'+0|A_5|$

2 Dựa vào ứng dụng Photomath

Photomath là một ứng dụng chạy trên nền tảng hệ điều hành Android hoặc IOS

Ứng dụng này hỗ trợ giải rất nhiều dạng toán khác nhau như Số học, Đại số, Giải tích, … và tất nhiên là có tính định thức

Ở đây mình sẽ hướng dẫn trên hệ điều hành Android, hệ điều hành IOS các bạn thực hiện tương tự

Bước 1 Truy cập vào cửa hàng Google Play tìm và cài đặt ứng dụng Photomath

Bước 2 Khởi động ứng dụng

Bước 3 Di chuyển Camera về phía của ma trận, chọn vào “nút tròn màu đỏ”, ứng dụng sẽ tự động nhận diện, tính toán và cho ra kết quả

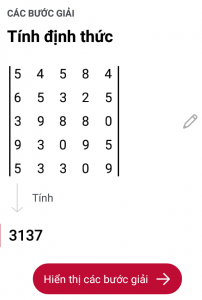
Nếu bạn muốn xem các bước tính toán trung gian thì hãy chọn vào Hiển thị các bước giải

Một số trường hợp ứng dụng không nhận diện hoặc nhận diện không chính xác ma trận thì bạn hãy nhập vào thông qua bàn phím

Bước 1 Chọn biểu tượng “máy tính cầm tay”

Bước 2 Chọn $f \int <>$

Bước 3 Chọn biểu tượng “ma trận”

Bước 4 Khai báo cấp của ma trận => chọn Chèn

Bước 5 Nhập ma trận và xem kết quả

3 Dựa vào dịch vụ trực tuyến Wolfram Alpha

Dịch vụ trực tuyến WolframAlpha hỗ trợ chúng ta thực hiện tính toán trên rất nhiều lĩnh vực như Mathematics, Science & Technology, Society & Culture, Every Life

Khả năng tính toán của Wolfram Alpha là rất lớn, nhiều bài toán phức tạp mà Photomath không giải được thì Wolfram Alpha vẫn giải được

Nâng cấp lên tài khoản Pro để hiển thị các bước tính toán trung gian
Chỉ với 69 000 VND bạn đã có thể sở hữu ngay ứng dụng chạy trên hệ điều hành Android

Bước 1 Nhập ma trận

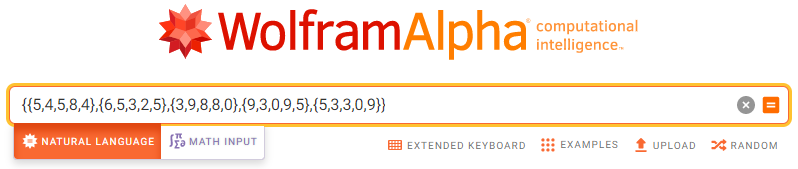
Phương pháp 1 Nhập theo ngôn ngữ tự nhiên {{5,4,5,8,4},{6,5,3,2,5},{3,9,8,8,0},{9,3,0,9,5},{5,3,3,0,9}}

Phương pháp 2 Nhập theo ngôn ngữ Toán học

Chọn MATH INPUT => chọn vào biểu tượng “ma trận cấp 5” => nhập các giá trị của ma trận

Bước 2 Nhấn phím Enter

WolframAlpha sẽ nhận diện và tự động tính toán cho ra các kết quả có liên quan như vết, định thức, ma trận nghịch đảo, …, giá trị Determinant chính là giá trị cần tìm

Vậy $|A|=3137$

Input	Bài toán đầu vào
Dimensions	Kích thước của ma trận
Trace	Vết của ma trận
Determinant	Định thức của ma trận
Inverse	Ma trận nghịch đảo
Characteristic polynomial	Đa thức đặc trưng
Eigenvalues	Giá trị riêng
Eigenvectors	Véctơ riêng
Diagonalization	Chéo hóa
Condition number	…

Ý nghĩa của một số kết quả đầu ra

Ngoài các phương pháp mà mình vừa giới thiệu các bạn cũng có thể tính bằng phần mềm Maple của Maplesoft

1 Dựa vào máy tính CASIO fx-580VN X

2 Dựa vào ứng dụng Photomath

3 Dựa vào dịch vụ trực tuyến Wolfram Alpha

Trả lời Hủy