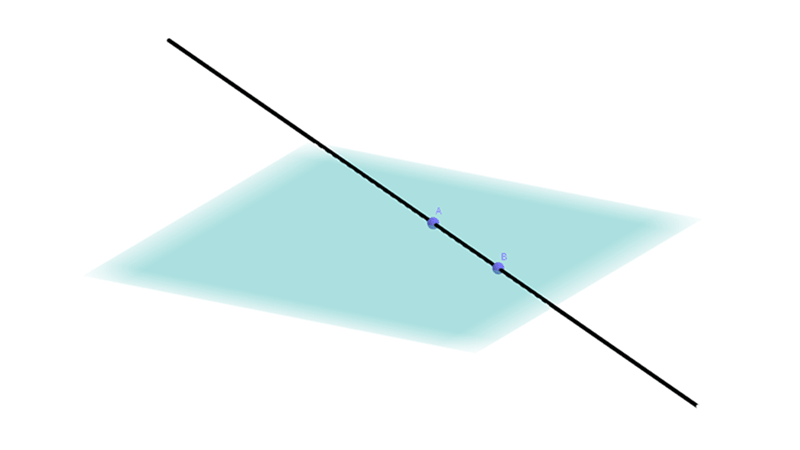
Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn xét vị trí tương đối giữa đường thẳng và mặt phẳng
Phương pháp Toán học thì đã có rất nhiều tài liệu hướng dẫn, mình không hướng dẫn lại
Phương pháp mà mình hướng dẫn ở đây chủ yếu dựa vào việc giải hệ ba phương trình ba ẩn tương ứng

1 Kiến thức Toán học
Trong không gian $Oxyz$ cho đường thẳng $(d)$ và mặt phẳng $(P)$ có phương trình tổng quát lần lượt là
$\left\{\begin{array}{c} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z+D_2=0 \end{array}\right.$ và $A_3x+B_3y+C_3z+D_3=0$
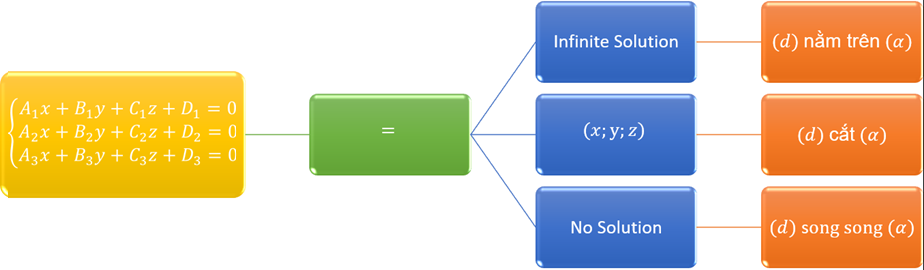
Xét hệ ba phương trình ba ẩn $\left\{\begin{array}{c} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z+D_2=0 \\ A_3x+B_3y+C_3z+D_3=0 \end{array}\right.$
- Hệ có vô số nghiệm thì $(d)$ nằm trên $(P)$
- Hệ có một nghiệm thì $(d)$ cắt $(P)$
- Hệ vô nghiệm thì $(d)$ song song $(P)$
2 Thủ thuật máy tính CASIO fx-580VN X
Bước 1 Giải hệ ba phương trình ba ẩn $\left\{\begin{array}{c} A_1x+B_1y+C_1z+D_1=0 \\ A_2x+B_2y+C_2z+D_2=0 \\ A_3x+B_3y+C_3z+D_3=0 \end{array}\right.$
Bước 2 Nếu máy tính thông báo
- Infinite Solution thì $(d)$ nằm trên $(P)$
- $(x; y; z)$ thì $(d)$ cắt $(P)$
- No Solution thì $(d)$ song song $(P)$
3 Ví dụ minh họa
Trong không gian $Oxyz$ cho đường thẳng $(d): \left\{\begin{array}{ccccc} x&=&-3&+&2t \\ y&=&-1&+&3t \\ z&=&1&+&2t \end{array}\right.$ và mặt phẳng $(P): 2x-2y+z+3=0$. Mệnh đề nào dưới đây là đúng?
A. $(d)$ nằm trên $(P)$
B. $(d)$ cắt $(P)$
C. $(d)$ vuông góc $(P)$
D. $(d)$ song song $(P)$
Dễ thấy phương trình tổng quát của đường thẳng $(d): \left\{\begin{array}{ccccc} 3x&-&2y&=&-7 \\ 2x&-&2z&=&-8 \end{array}\right.$
Bước 1 Giải hệ phương trình $\left\{\begin{array}{ccccccc} 3x&-&2y&+&0z&=&-7 \\ 2x&+&0y&-&2z&=&-8 \\ 2x&-&2y&+&1z&=&-3 \end{array}\right.$
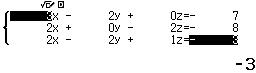
Bước 2 Nhấn phím =

Vậy $(d)$ nằm trên $(P)$
Trong không gian $Oxyz$ cho đường thẳng $(d): \left\{\begin{array}{CCCCC} x&=&1&-&2t \\ y&=&3t&-&1 \\ z&=&1&-&t \end{array}\right.$ và mặt phẳng $(P): 2x-3y+z-6=0$. Mệnh đề nào dưới đây là đúng?
A. $(d)$ nằm trên $(P)$
B. $(d)$ cắt $(P)$
C. $(d)$ vuông góc $(P)$
D. $(d)$ song song $(P)$
Dễ thấy phương trình tổng quát của đường thẳng $(d): \left\{\begin{array}{ccccc} 3x&+&2y&=&1 \\ -x&+&2z&=&1 \end{array}\right.$
Bước 1 Giải hệ phương trình $\left\{\begin{array}{ccccccc} 3x&+&2y&+&0z&=&1 \\ -1x&+&0y&+&2z&=&1 \\ 2x&-&3y&+ &1z&=&6\end{array}\right.$
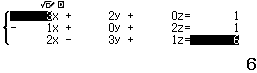
Bước 2 Nhấn phím =



Suy ra $(d)$ cắt $(P)$
Bước 3 Tính tích có hướng của $\vec{u_d}=(-2, 3, -1)$ và $\vec{n_p}=(2, -3, 1)$
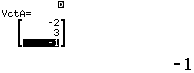
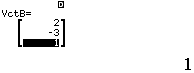
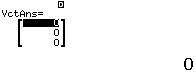
Vậy $(d)$ vuông góc $(P)$
Trong không gian $Oxyz$ cho đường thẳng $(d):\dfrac{x+1}{1}=\dfrac{y}{-3}=\dfrac{z-5}{-1}$ và mặt phẳng $(P): 3x-3y+2z+6=0$. Mệnh đề nào dưới đây là đúng?
A. $(d)$ nằm trên $(P)$
B. $(d)$ cắt $(P)$
C. $(d)$ vuông góc $(P)$
D. $(d)$ song song $(P)$
Dễ thấy phương trình tổng quát của đường thẳng $(d): \left\{\begin{array}{ccccc} 3x&+&y&=&-3 \\ x&+&z&=&4 \end{array} \right.$
Bước 1 Giải hệ phương trình $\left\{\begin{array}{ccccccc} 3x&+&1y&+&0z&=&-3 \\ 1x&+&0y&+&1z&=&4 \\ 3x&-&3y&+ &2z&=&-6\end{array}\right.$
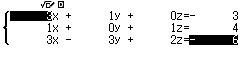
Bước 2 Nhấn phím =



Suy ra $(d)$ cắt $(P)$
Bước 3 Tính tích có hướng của $\vec{u_d}=(1, -3, -1)$ và $\vec{n_p}=(3, -3, 2)$
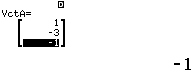
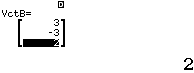
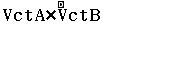
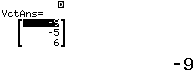
Vậy $(d)$ không vuông góc $(P)$
Trong không gian $Oxyz$ cho đường thẳng $(d): \left\{\begin{array}{CCC} \dfrac{3}{2}y&=&\dfrac{3}{2} \\\\ -\dfrac{1}{2}x&=&0 \end{array} \right.$ và mặt phẳng $(P): 2x-y+2=0$. Mệnh đề nào dưới đây là đúng?
A. $(d)$ nằm trên $(P)$
B. $(d)$ cắt $(P)$
C. $(d)$ vuông góc $(P)$
D. $(d)$ song song $(P)$
Bước 1 Giải hệ phương trình $\left\{\begin{array}{ccccccc} 0x&+&\dfrac{3}{2}y&+&0z&=&\dfrac{3}{2} \\ -\dfrac{1}{2}x&+ &0y&+&0z&=&0 \\ 2x&-&1y&+&0z&=&-2 \end{array}\right.$
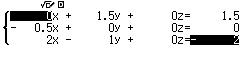
Bước 2 Nhấn phím =
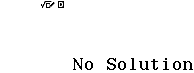
Vậy $(d)$ song song $(P)$
4 Chú ý
4.1 Phương trình đường thẳng không đưa được về dạng tổng quát
Nếu phương trình đường thằng được cho dưới dạng tham số hoặc chính tắc thì bạn cần chuyển sang dạng tổng quát trước khi áp dụng thủ thuật
$\left\{\begin{array}{c} x=x_{0}+pt \\ y=y_{0}+qt \\ z=z_{0}+rt \end{array}\right. \Leftrightarrow \dfrac{x-x_{0}}{p}=\dfrac{y-y_{0}}{q}=\dfrac{z-z_{0}}{r} \Leftrightarrow \left\{\begin{array}{c} \dfrac{x-x_{0}}{p}=\dfrac{y-y_{0}}{q} \\ \dfrac{x-x_{0}}{p}=\dfrac{z-z_{0}}{r} \end{array}\right.$
Trường hợp không chuyển được vì $p.q.r=0$ thì sử dụng kiến thức Toán học bên dưới để giải quyết
Trong không gian $Oxyz$ cho đường thẳng $(d)$ đi qua điểm $A$ và có véctơ chỉ phương $\vec{u_d}$, mặt phẳng $(P)$ có véctơ pháp tuyến $\vec{n_p}$
Khi đó
- $(d)$ nằm trên $(P)$ khi và chỉ khi $~$ $\left\{\begin{array}{c} \vec{u_d} \cdot \vec{n_p}=0 \\ A \in (P) \end{array}\right.$
- $(d)$ cắt $(P)$ khi và chỉ khi $\vec{u_d} \cdot \vec{n_p} \neq 0$
- $(d)$ song song $(P)$ khi và chỉ khi $\left\{\begin{array}{c} \vec{u_d} \cdot \vec{n_p}=0 \\ A \notin (P) \end{array}\right.$
4.2 Đường thẳng vuông góc với mặt phẳng
Nếu $[\vec{u_d}, \vec{n_p}]=\vec{0}$ thì $(d)$ vuông góc $(P)$
4.3 Véc tơ chỉ phương của đường thẳng
Phương trình tổng quát của đường thẳng $(d)$ có một véc tơ chỉ phương là $\vec{u_d}=\left(\left|\begin{array}{cc}B_1&C_1 \\ B_2&C_2\end{array}\right|, \left|\begin{array}{cc}C_1&A_1 \\ C_2&A_2\end{array}\right|, \left|\begin{array}{cc}A_1&B_1 \\ A_2&B_2\end{array}\right|\right)$