Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước tìm ước chung lớn nhất, bội chung nhỏ nhất của hai số, ba số, bốn số, …, bằng máy tính cầm tay CASIO fx 580 VN X
1 Ước chung lớn nhất
Để tìm ước chung lớn nhất của hai số $a_1, a_2$ ta sử dụng phím GCD với công thức $GCD(a_1, a_2)$
Để tìm ước chung lớn nhất của ba số $a_1, a_2, a_3$ ta sử dụng phím GCD với công thức $GCD(a_1, GCD(a_2, a_3))$
Chẳng hạn 1 mình cần tìm ước chung lớn nhất của hai số $479, 686$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím $\times$
Bước 2 nhập số $479$
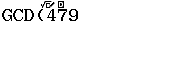
Bước 3 nhấn phím SHIFT => nhấn phím )
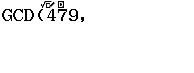
Bước 4 nhập số $686$
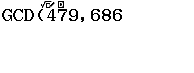
Bước 5 nhấn phím =
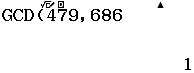
Vậy $UCLN(479, 686)=1$
Chẳng hạn 2 mình cần tìm ước chung lớn nhất của ba số $909, 153, 773$ thì thực hiện tuần tự theo các bước bên dưới
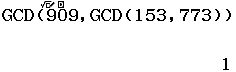
Vậy $UCLN(909, 153, 773)=1$
Xem thêm Ước chung lớn nhất
2 Bội chung nhỏ nhất
Để tìm bội chung nhỏ nhất của hai số $a_1, a_2$ ta sử dụng phím LCM với công thức $LCM(a_1, a_2)$
Để tìm bội chung nhỏ nhất của ba số $a_1, a_2, a_3$ ta sử dụng phím LCM với công thức $LCM(a_1, LCM(a_2, a_3))$
Chẳng hạn 3 mình cần tìm bội chung nhỏ nhất của hai số $759, 539$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhấn phím ALPHA => nhấn phím $\div$
Bước 2 nhập số $759$
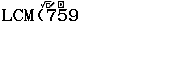
Bước 3 nhấn phím SHIFT => nhấn phím )
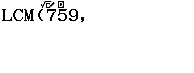
Bước 4 nhập số $539$
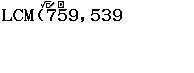
Bước 5 nhấn phím =
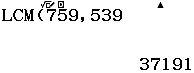
Vậy $BCNN(759, 539)=37~191$
Chẳng hạn 4 mình cần tìm bội chung nhỏ nhất của ba số $13, 690, 219$ thì thực hiện tuần tự theo các bước bên dưới
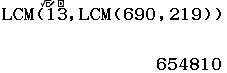
Vậy $BCNN(13, 690, 219)=654~810$
Xem thêm Bội chung nhỏ nhất
3 Lời kết
Phím GCD và LCM của máy tính cầm tay CASIO fx 580 VN X mặc dù cho phép chúng ta xác định nhanh ước chung lớn nhất và bội chung nhỏ nhất của hai số, ba số, bốn số, …
Tuy nhiên với những số có giá trị lớn thì bạn nên tìm ước chung lớn nhất bằng thuật giải Euclid sau đó áp dụng công thức $LCM(A, B)=\frac{AB}{GCD(A, B)}$ để tìm bội chung nhỏ nhất
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
