Xin chào tất cả các bạn, hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước thực hiện thủ thuật khai triển và rút gọn đa thức một ẩn với hệ số nguyên bằng máy tính cầm tay CASIO fx 580 VN X
Như các bạn đã viết, thao tác khai triển và rút gọn đa thức là một trong những thao tác thường nhất trong quá trình làm toán
Thao tác trên tuy không khó khăn nhưng với những đa thức phức tạp thì cũng tốn khá nhiều thời gian và công sức
Lúc bấy giờ, việc khai triển và rút gọn đa thức bằng máy tính cầm tay sẽ là một giải pháp tối ưu
1 Bật dấu phân cách ba chữ số
Khi dấu phân cách ba chữ số được bật thì kết quả tính toán sẽ tự động được tách thành từng bộ ba theo chiều từ phải sang trái
Bước 1 nhấn phím SHIFT => nhấn phím MENU

Bước 2 nhấn phím ![]() => nhấn phím
=> nhấn phím ![]()

Bước 3 nhấn phím 4

Bước 4 nhấn phím 1

2 Các bước khai triển và rút gọn
Bước 1 nhập đa thức
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
Bước 3 phân tích giá trị và dự đoán đa thức cần tìm
Bước 3.1 phân tích giá trị theo chiều từ phải sang trái theo nguyên tắc nếu có một bộ ba lớn bất thường thì lấy 1000 trừ cho bộ ba đó đồng thời cộng 1 vào bộ ba ngay bên trái
Bước 3.2 dự đoán đa thức cần tìm
Bước 4 nhập “đa thức đã cho trừ đa thức cần tìm” => nhấn phím CALC => nhấn phím SHIFT => nhấn phím . => nhấn phím = => nhấn phím =
- Nếu kết quả bằng 0 thì dự đoán chính xác
- Nếu kết quả khác 0 thì dự đoán không chính xác
3 Thực hành khai triển và rút gọn
Ví dụ 1 khai triển và rút gọn đa thức $(x+1)(x+2)+(3x^2+x+6)(x+7)$
Bước 1 nhập đa thức
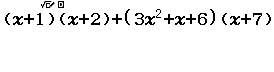
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
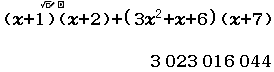
Bước 3 phân tích và dự đoán
- $3~023~016~044$ được phân tích thành $3~23~16~44$
- $3x^3+23x^2+16x+44$
Bước 4 kiểm tra
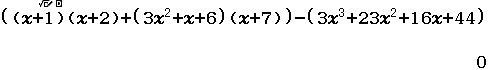
Vậy $(x+1)(x+2)+(3x^2+x+6)(x+7)=3x^3+23x^2+16x+44$
Ví dụ 2 Khai triển và rút gọn đa thức $(5x-3)(x^2+6x-7)+10x-21$
Bước 1 nhập đa thức
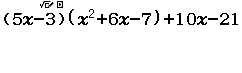
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
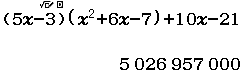
Bước 3 phân tích và dự đoán
- $5~026~957~000$ được phân tích thành $5~~~026+1~~~957-1000~~~000$ hay $5~27~-43~0$
- $5x^3+27x^2-43x$
Bước 4 kiểm tra
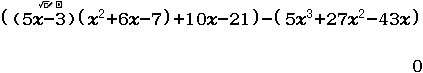
Vậy $(5x-3)(x^2+6x-7)+10x-21=5x^3+27x^2-43x$
Ví dụ 3 Khai triển và rút gọn đa thức $(x^2-3x+7)(x+2)$
Bước 1 nhập đa thức
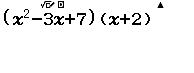
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
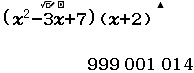
Bước 3 phân tích và dự đoán
- $999~001~014$ được phân tích thành $1~~~999-1000~~~001~~~014$ hay $1~-1~1~14$
- $x^3-x^2+x+14$
Bước 4 kiểm tra
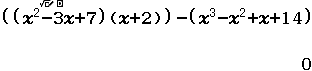
Vậy $(x^2-3x+7)(x+2)=x^3-x^2+x+14$
Ví dụ 4 Khai triển và rút gọn đa thức $(x^2-3x-7)(x+2)$
Bước 1 nhập đa thức
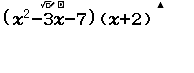
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
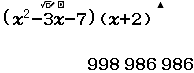
Bước 3 phân tích và dự đoán
- $998~986~986$ được phân tích thành $1~~~998+1-1000~~~986+1-1000~~~986-1000$ hay $1~-1~-13~-14$
- $x^3-x^2-13x-14$
Bước 4 kiểm tra
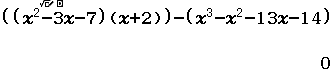
Vậy $(x^2-3x-7)(x+2)=x^3-x^2-13x-14$
Ví dụ 5 Khai triển và rút gọn đa thức $(x+5)(x+3)(x-7)-(4x^2-3x+7)(x-1)$
Bước 1 nhập đa thức
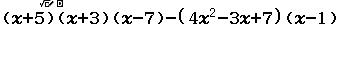
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
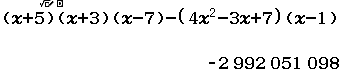
Bước 3 phân tích và dự đoán
- $2~992~051~098$ được phân tích thành $2+1~~~992-1000~~~051~~~098$ hay $3~-8~51~98$
- Vì giá trị tìm được ở Bước 2 nhỏ hơn không nên kết quả phân tích cuối cùng phải là $-3~8~-51~-98$
- $-3x^3+8x^2-51x-98$
Bước 4 kiểm tra
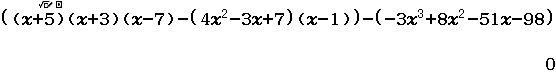
Vậy $(x+5)(x+3)(x-7)-(4x^2-3x+7)(x-1)=-3x^3+8x^2-51x-98$
Ví dụ 6 Khai triển và rút gọn đa thức $(x^2+2x+3)^2$
Bước 1 nhập đa thức
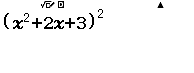
Bước 2 nhấn phím CALC => nhập 1000 => nhấn phím =
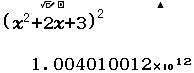
Bước 3 phân tích và dự đoán
- $1.004010012 \times 10^{12} =1~004~010~012~009$ được phân tích thành $1~4~10~12~9$
- $x^4+4x^3+10x^2+12x+9$
Xem thêm Xử lý kết quả tính toán tràn màn hình
Bước 4 kiểm tra
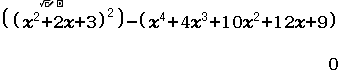
Vậy $(x^2+2x+3)^2=x^4+4x^3+10x^2+12x+9$
4 Lời kết
Mặc dù thủ thuật khai triển và rút gọn đa thức trên máy tính cầm tay CASIO fx 580 VN X chỉ áp dụng được với những đa thức một biến và có hệ số nguyên nhưng đây vẫn là một thủ thuật tuyệt với
Trong thời gian tới mình sẽ nghiên cứu và phát triển thêm thủ thuật này theo hướng áp dụng được cho các đa thức một biến có hệ số hữu tỉ hoặc đa thức hai biến
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
Nguyên tác
Trần Ngọc Ánh Phương