Đổi số phức từ đại số sang lượng giác bằng CASIO fx 880 BTG

Xin chào tất cả các bạn

Việc chuyển đổi số phức từ dạng đại số sang dạng lượng giác bằng kiến thức Toán học mặc dù đã có công thức nhưng vẫn tốn khá nhiều công sức và thời gian

Biết được khó khăn trên, hôm nay mình sẽ hướng dẫn các bạn cách chuyển đổi số phức từ dạng đại số sang dạng lượng giác bằng máy tính cầm tay CASIO fx 880 BTG

fx 880 BTG sẽ giúp chúng ta chuyển đổi một cách chính xác và nhanh chóng

1 Sơ lược về kiến thức Toán học

Mọi số phức đều có thể chuyển đổi từ dạng đại số sang dạng lượng giác

Mọi số phức đều có dạng đại số là và dạng lượng giác là

Chỉ cần nhập vào, fx 880 BTG sẽ tự động tìm ra và , lúc bấy giờ bạn chỉ cần “lắp ráp” lại là xong

2 Các bước thực hiện

Bước 1 cài đặt đơn vị góc là ra đi an

Bước 2 mở ứng dụng số phức Complex

Bước 3 nhập số phức

Phần tử đơn vị ảo i được nhập vào bằng cách nhấn phím SHIFT => nhấn phím 9

Bước 4 nhấn phím EXE

Bước 5 nhấn phím FORMAT => chọn Polar Coord

3 Ví dụ minh họa

Chẳng hạn mình cần chuyển đổi số phức sang dạng lượng giác thì thực hiện tuần tự theo các bước bên dưới

Bước 1 cài đặt đơn vị góc là ra đi an

Nhấn phím SETTINGS => chọn Calc Setting => nhấn phím OK => chọn Radian => nhấn phím OK => nhấn phím AC

Bước 2 mở ứng dụng số phức Complex

Nhấn phím HOME => chọn Complex => nhấn phím OK

Bước 3 nhập số phức

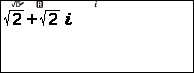
Bước 4 nhấn phím EXE

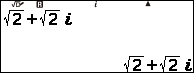
Bước 5 nhấn phím FORMAT => chọn Polar Coord => nhấn phím EXE

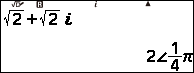
Suy ra và

Vậy dạng lượng giác của số phức là

4 Lời kết

Như các bạn đã biết việc khai căn bậc ba của một số phức ở dạng đại số không phải chuyện đơn giản

Mặc dù máy tính cầm tay CASIO fx 880 BTG vẫn chưa hỗ trợ chúng ta khai căn bậc ba của số phức nhưng hỗ trợ chúng ta chuyển đổi số phức từ dạng đại số sang dạng lượng giác đã là một đều tuyệt vời

Sau khi chuyển đổi xong các bạn chỉ cần áp dụng công thức

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo