Phương trình đường thẳng, đường tròn và đường cong Parabol là một trong những phương trình thường gặp trong chương trình Toán học Trung học Phổ thông
Tùy thuộc vào các dữ kiện cho trước mà sẽ có các cách viết khác nhau, điểm đi qua là một trong những dữ kiện thường gặp nhất
Hôm này mình sẽ hướng dẫn các bạn viết phương trình đường thẳng đi qua hai điểm, đường tròn hoặc đường cong Parabol đi qua ba điểm bằng máy tính CASIO fx-580VN X
1 Phương trình đường thẳng đi qua hai điểm
Có nhiều phương pháp để viết phương trình đường thẳng đi qua hai điểm cho trước
Trong phạm vi của bài viết này mình sẽ hướng dẫn các bạn viết bằng cách giải hệ hai phương trình hai ẩn
Giả sử phương trình đường thẳng cần tìm có dạng $y=ax+b$ và tọa độ của hai điểm đi qua là $(x_1, y_1), (x_2, y_2)$
Khi đó $a, b$ là nghiệm của hệ phương trình $\left\{\begin{array}{l}y_1=ax_1+b\\y_2=ax_2+b\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}ax_1+b=y_1\\ax_2+b=y_2\end{array}\right.$
Nếu phương trình đường thẳng cần tìm trùng hoặc song song với trục tung thì phương pháp này không khả dụng
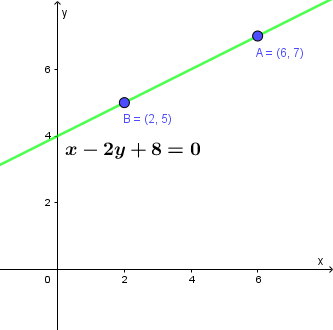
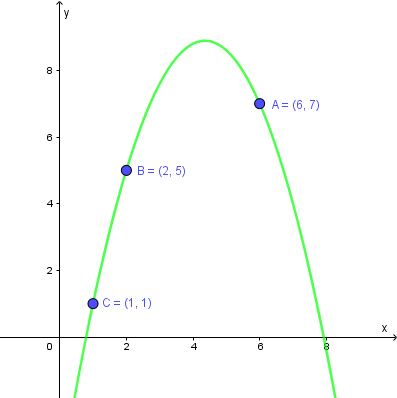
Viết phương trình đường thẳng đi qua hai điểm $A=(6; 7)$, $B=(2; 5)$
Bước 1 Chọn phương thức tính toán Equation/ Func
Bước 2 Chọn Simul Equation
Bước 3 Nhấn phím 2
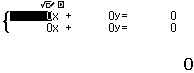
Bước 4 Nhập các hệ số của hệ phương trình $\left\{\begin{array}{l}6a+b=7\\2a+b=5\end{array}\right.$
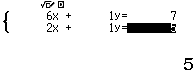
Bước 5 Nhấn phím =
Vậy phương trình đường thẳng cần tìm là $y=\dfrac{1}{2}x+4$
2 Phương trình đường tròn
Giả sử phương trình đường tròn cần tìm có dạng $x^2+y^2-2ax-2by+c=0$ và tọa độ ba điểm đi qua $(x_1; y_1)$, $(x_2; y_2)$, $(x_3; y_3)$
Khi đó $a, b, c$ là nghiệm của hệ phương trình
$\left\{\begin{array}{l}x_1^2+y_1^2-2ax_1-2by_1+c=0\\\\x_2^2+y_2^2-2ax_2-2by_2+c=0\\\\x_3^2+y_3^2-2ax_3-2by_3+c=0\end{array}\right. \Leftrightarrow \left\{\begin{array}{lll}-2ax_1-2by_1+c=-(x_1^2+y_1^2)\\\\-2ax_2-2by_2+c=-(x_2^2+y_2^2)\\\\-2ax_3-2by_3+c=-(x_3^2+y_3^2)\end{array}\right.$
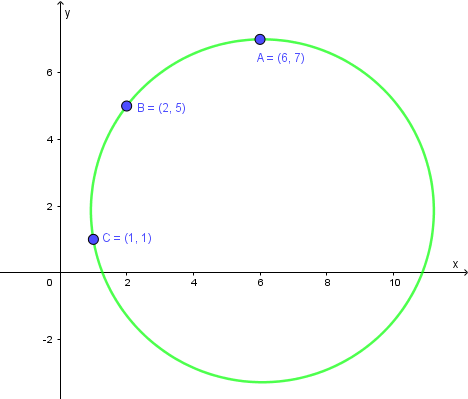
Viết phương trình đường tròn đi qua ba điểm $A=(6; 7)$, $B=(2; 5)$, $C=(1; 1)$
Bước 1 Chọn phương thức tính toán Equation/ Func
Bước 2 Chọn Simul Equation
Bước 3 Nhấn phím 3
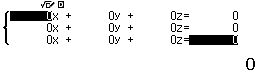
Bước 4 Nhập các hệ số của hệ phương trình $\left\{\begin{array}{lrrrr}-&12a~-&14b~+&c=-&85\\-&4a~-&10b~+&c=-&29\\-&2a~-&2b~+&c=-&2\end{array}\right.$
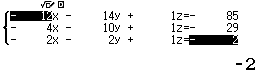
Bước 5 Nhấn phím =
Vậy phương trình đường tròn cần tìm là $x^2+y^2-2.\dfrac{85}{14}x-2.\dfrac{13}{7}y+\dfrac{97}{7}=0$
3 Phương trình cong Parabol
Giả sử phương trình đường cong Parabol cần tìm có dạng $y=ax^2+bx+c$ và tọa độ của ba điểm đi qua là $(x_1; y_1)$, $(x_2; y_2)$, $(x_3; y_3)$
Khi đó $a, b, c$ là nghiệm của hệ phương trình
$\left\{\begin{array}{l}y_1=ax_1^2+bx_1+c\\\\y_2=ax_2^2+bx_2+c\\\\y_3=ax_3^2+bx_3+c\end{array}\right. \Leftrightarrow \left\{\begin{array} {l}ax_1^2+bx_1+c=y_1\\\\ax_2^2+bx_2+c=y_2\\\\ax_3^2+bx_3+c=y_3\end{array}\right.$
Viết phương trình đường cong Parabol đi qua ba điểm $A=(6; 7)$, $B=(2; 5)$, $C=(1; 1)$
Bước 1 Chọn phương thức tính toán Equation/ Func
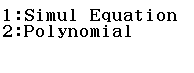
Bước 2 Chọn Simul Equation
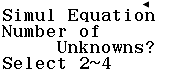
Bước 3 Nhấn phím 3
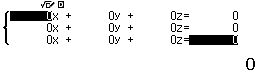
Bước 4 Nhập các hệ số của hệ phương trình $\left\{\begin{array}{rrrr}36a~+&6b~+&c=&7\\4a~+&2b~+&c=&5\\a~+&b~+&c=&1\end{array}\right.$
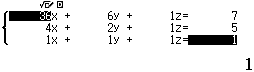
Bước 5 Nhấn phím =
Vậy phương trình đường cong Parabol cần tìm là là $y=-\dfrac{7}{10}x^2+\dfrac{61}{10}x-\dfrac{22}{5}$