Ai trong chúng ta cũng biết việc giải phương trình nói chung hay phương trình lượng giác nói riêng là tìm tất cả các giá trị của ẩn thỏa mãn phương trình đã cho
Tương ứng với mỗi loại phương trình sẽ có các cách giải khác nhau, với phương trình lượng giác thì thường giải bằng cách đưa về giải các phương trình lượng giác cơ bản
Cụ thể là đưa về một trong bốn phương trình $\sin x = a$, $\cos x = a$, $\tan x = a$ và $\cot x =a$ với $a \in R$
Trong phạm vi ngắn gọn của bài viết này, mình sẽ hướng dẫn các bạn sử dụng máy tính CASIO fx-580VN X hỗ trợ giải một số lớp phương trình lượng giác thường gặp
1 Công thức nghiệm của các phương trình lượng giác cơ bản
- $\sin f(x) = \sin g(x) \Leftrightarrow \left[\begin{array}{ll} f(x) = g(x) + k 2\pi\\ f(x) = \pi – g(x) + k 2\pi \end{array}\right.$ với $k \in Z$
- $\cos f(x) = \cos g(x) \Leftrightarrow f(x) = \pm g(x) + k 2\pi$ với $k \in Z$
- $\tan f(x) = \tan g(x) \Rightarrow f(x) = g(x) + k \pi$ với $k \in Z$
- $\cot f(x) = \cot g(x) \Rightarrow f(x) = g(x) + k \pi$ với $k \in Z$
Trong cùng một công thức nghiệm của một phương trình lượng giác không được dùng đồng thời nhiều đơn vị góc
2 Phương trình lượng giác cơ bản
Máy tính CASIO fx-580VN X có thể sử dụng để hỗ trợ giải một số lớp phương trình lượng giác. Tuy nhiên đối với phương trình $\sin x = a$ máy tính chỉ cho kết quả là $\arcsin a$
Lúc bấy giờ theo công thức nghiệm đã biết chúng ta sẽ kết luận các nghiệm của phương trình này là $x=\arcsin a + k 2\pi$ và $x= \pi -\arcsin a + k 2\pi$ với $k \in Z$
- Nếu $\arcsin a$ có giá trị là một “số đẹp” thì ghi số đó
- Nếu $\arcsin a$ có giá trị là một “số xấu” thì ghi $\arcsin a$
Thực hiện tương tự đối với các phương trình $\cos x =a$, $\tan x = a$ và $\cot x = a$
Chúng ta nên thiết lập đơn vị góc mặc định là Radian trước khi giải các phương trình lượng giác bằng máy tính CASIO fx-580VN X
Giải phương trình $\sin x=\dfrac{1}{2}$
Bước 1 Nhấn phím $\sin^{-1}$

Bước 2 Nhập $\dfrac{1}{2}$

Bước 3 Nhấn phím =

Vậy nghiệm của phương trình đã cho là $x=\dfrac{\pi}{6}+k2\pi$ và $x=\dfrac{5\pi}{6}+k2\pi$ với $k \in Z$
Giải phương trình $\cos x=\dfrac{1}{3}$
Bước 1 Nhấn phím $\cos^{-1}$

Bước 2 Nhập $\dfrac{1}{3}$

Bước 3 Nhấn phím =

Vậy nghiệm của phương trình đã cho là $x=\pm \arccos\left(\dfrac{1}{3}\right)+k2\pi$ với $k \in Z$
Giải phương trình $\tan(3x+15^o)=\sqrt{3}$
Bước 1 Nhấn phím $\tan^{-1}$

Bước 2 Nhập $\sqrt{3}$
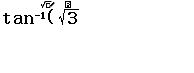
Bước 3 Nhấn phím =
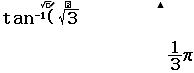
Bước 4 Sử dụng tính năng SOLVE giải phương trình $3x+\dfrac{\pi}{12}=\dfrac{\pi}{3}$
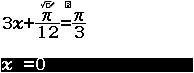
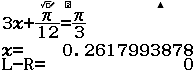

Vậy nghiệm của phương trình đã cho là $x=\dfrac{\pi}{12}+k\pi$ với $k \in Z$
- Dễ thấy $15^o=\dfrac{\pi}{12}^r$
- Thao tác chia nghiệm tìm được cho $\pi$ là để tìm ra nghiệm chính xác
Giải phương trình $\cot4x=\cot\dfrac{2\pi}{7}$
Sử dụng tính năng SOLVE giải phương trình $4x=\dfrac{2\pi}{7}$



Vậy nghiệm của phương trình đã cho là $x=\dfrac{\pi}{14}+k\pi$ với $k \in Z$
3 Phương trình bậc nhất đối với một hàm số lượng giác
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng $at+b=0$ trong đó $a, b$ là các hằng số $(a \neq 0)$ và $t$ là một trong các hàm số $\sin, \cos, \tan$ và $\cot$
Phương pháp giải
- Chuyển vế
- Chia hai vế của phương trình cho $a$ để đưa phương trình về phương trình lượng giác cơ bản
- Giải phương trình lượng giác cơ bản vừa tìm được
Giải phương trình $3\cos x+5=0$
Biến đổi sơ cấp $3\cos x+5=0 \Leftrightarrow \cos x=-\dfrac{5}{3}$
Dễ thấy phương trình đã cho vô nghiệm, thật vậy
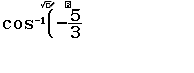

Giải phương trình $\sqrt{3}\tan x+1=0$
Bước 1 Biến đổi sơ cấp $\sqrt{3}\tan x+1=0 \Leftrightarrow \tan x=-\dfrac{1}{\sqrt{3}}$
Bước 2 Giải phương trình $\tan x=-\dfrac{1}{\sqrt{3}}$
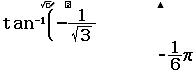
Vậy nghiệm của phương trình đã cho là $x=-\dfrac{\pi}{6}+k\pi$ với $k \in Z$
4 Phương trình bậc hai đối với một hàm số lượng giác
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng $at^2+bt+c=0$ trong đó $a, b, c$ là các hằng số $(a \neq 0)$ và $t$ là một trong các hàm số $\sin, \cos, \tan$ và $\cot$
Phương pháp giải
- Đặt biểu thức lượng giác bằng ẩn phụ
- Đặt điều kiện cho ẩn phụ (nếu có)
- Giải phương trình bậc hai vừa tìm được
- Giải các phương trình lượng giác cơ bản vừa tìm được
Giải phương trình $2 \sin^2(x) + 3 \sin(x) – 2 = 0$
Bước 1 Đặt $t = sin(x)$ với $t \in [-1; 1]$ phương trình trở thành $2 t^2 + 3 t – 2 = 0$
Bước 2 Giải phương trình bậc hai $2 t^2 + 3 t – 2 = 0$
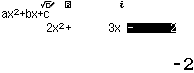
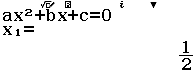
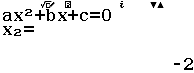
Nghiệm $t=\dfrac{1}{2} \in [-1; 1]$ nhận, nghiệm $t=-2 \notin [-1; 1]$ loại
Tập giá trị của hàm $\sin$ và hàm $\cos$ là $[-1; 1]$
Bước 3 Giải phương trình $\sin x=\dfrac{1}{2}$

Vậy nghiệm của phương trình đã cho là $x=\dfrac{\pi}{6}+k2\pi$ và $x=\dfrac{5\pi}{6}+k2\pi$ với $k \in Z$
Giải phương trình $3 \cot^2(x) – 5 \cot(x) – 7 = 0$
Bước 1 Đặt $t = \cot(x)$ phương trình đã cho trở thành $3t^2-5t-7=0$
Bước 2 Giải phương trình bậc hai $3t^2-5t-7=0$
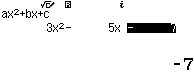
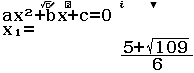
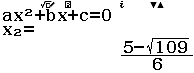
Bước 3 Giải phương trình $\cot x=\dfrac{5+\sqrt{109}}{6}$

Bước 4 Giải phương trình $\cot x=\dfrac{5-\sqrt{109}}{6}$
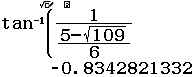
Vậy nghiệm của trình đã cho là $x=$ arccot $\dfrac{5+\sqrt{109}}{6}+k\pi$ và $x=$ arccot $\dfrac{5-\sqrt{109}}{6}+k\pi$ với $k \in Z$




yuyuyu