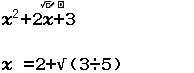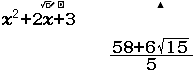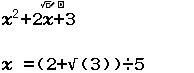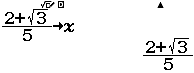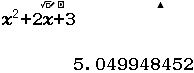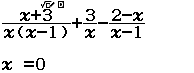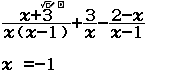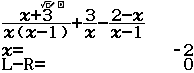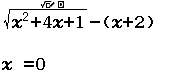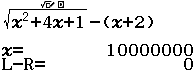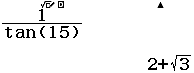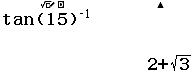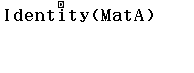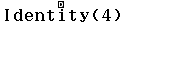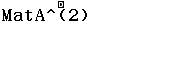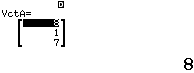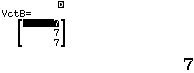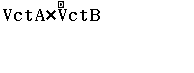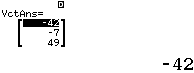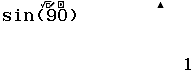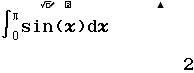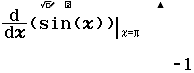Xin chào tất cả các bạn, hôm nay mình sẽ liệt kê một số sai lầm thường gặp khi sử dụng máy tính CASIO fx-580VN X
Với mỗi sai lầm mình đều cho ví dụ minh họa, chỉ ra nguyên nhân và đề xuất hướng khắc phục
Tất cả những đều này sẽ giúp các bạn tránh được những sai lầm không đáng có, góp phần nâng cao hiệu quả học tập, giảng dạy
1 Sai lầm trong các phương thức tính toán
1.1 Tính toán cơ bản
1.1.1 Tính năng CALC
Tính năng CALC là một trong những tính năng được sử dụng thường xuyên nhất
Tính năng này cho phép chúng ta tính giá trị của một biểu thức bất kì
Tính giá trị của biểu thức $x^2+2x+3$ khi $x=\dfrac{2+\sqrt{3}}{5}$
Bước 1 Nhập biểu thức $x^2+2x+3$
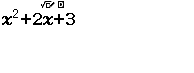
Bước 2 Nhấn phím CALC => nhập $\dfrac{2+\sqrt{3}}{5}$ => nhấn phím =
Vậy giá trị cần tìm là $\quicklatex{color=”#cf2e2e”} \dfrac{58+6 \sqrt{15}}{5}$
Kết luận trên là SAI vì khi nhấn phím CALC máy tính chuyển từ MathI sang LineI nên giá trị $2+\surd(3 \div 5)$ được hiểu là $\dfrac{10+ \sqrt{15}}{5}$
Khi nhập các giá trị có chứa phân số, căn thức bạn cần chú ý mở, đóng các dấu ngoặc cho chính xác hoặc gán vào biến nhớ trước nhập biểu thức
Vậy giá trị cần tìm là $\approx 5.049948452$
1.1.2 Tính năng SOLVE
Tương tự như tính năng CALC, tính năng SOLVE cũng là một trong những tính năng được sử dụng thường xuyên nhất
Tính năng SOLVE cho phép dò tìm nghiệm của một phương trình bất kì
Giải phương trình $\dfrac{x+3}{x(x-1)}+\dfrac{3}{x}-\dfrac{2-x}{x-1}=0$
Bước 1 Nhập vế trái của phương trình $\dfrac{x+3}{x(x-1)}+\dfrac{3}{x}-\dfrac{2-x}{x-1}$
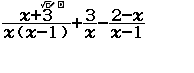
Bước 2 Nhấn phím SOLVE => nhập giá trị $x$ ban đầu (mình sẽ nhập $0$) => nhấn phím = > nhấn phím =
Vậy phương trình đã cho vô nghiệm
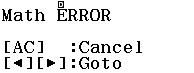
Kết luận trên là SAI vì phương trình đã cho có một nghiệm là $-2$
Thông báo Cannot Solve không có nghĩa là phương trình vô nghiệm, có hai nguyên nhân dẫn đến thông báo này
- Giá trị $x$ ban đầu không phù hợp
- Phương trình vô nghiệm
Hiện tại vẫn chưa có phương pháp nào giúp chúng ta phân biệt được thông báo trên đến từ nguyên nhân nào
Khi gặp thông báo Cannot Solve bạn hãy thử dò tìm lại với một vài giá trị $x$ ban đầu khác thuộc tập xác định của phương trình
Với giá trị $x$ ban đầu bằng $-1$ phương trình đã cho có một nghiệm là $-2$
Vậy phương trình đã cho có một nghiệm là $-2$
Giải phương trình $\sqrt{x^2+4x+1}-(x+2)=0$
Vậy phương trình đã cho có nghiệm là $ \quicklatex{color=”#cf2e2e”} 10~000~000$
Kết luận này là SAI vì phương trình vô nghiệm
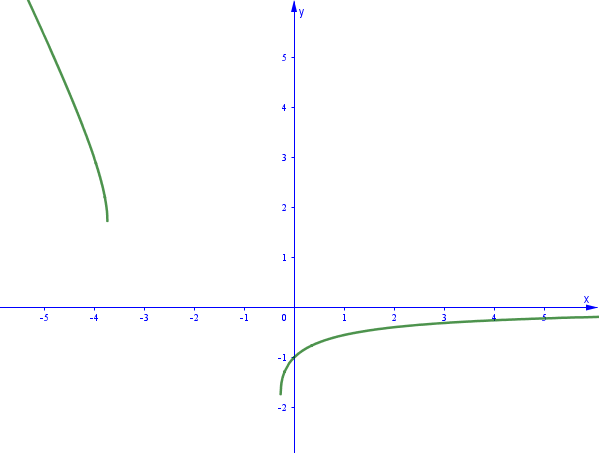
Thật vậy $\sqrt{x^2+4x+1}-(x+2)=0 \Leftrightarrow \left\{ \begin{array}{l} x \geq -2\\ 1=4 \end{array}\right.$
Nguyên nhân
$f(x): \sqrt{x^2+4x+1}$ và $g(x): x+2$
Suy ra $f(10^7)=\sqrt{100~000~040~000~001}$ và $g(10^7) = 10~000~002$
Xét biểu thức $\sqrt{100~000~040~000~001}-10~000~002 = $ 1.499 999 700 000 071 249 981 250 005 268 748 451 250 470 413 916 020 359 010 $\cdots \times 10^{-7}$
Giá trị vừa tìm được tiệm cận giá trị $0$ nên máy tính mới hiểu nhằm $10^7$ là nghiệm của phương trình
Giải pháp
Nếu phương trình có dạng $\sqrt{ax^2+bx+c}=dx+e$ trong đó $a=d^2$ và $b=2de$ và $c \neq e^2$ thì máy tính sẽ dò tìm được nghiệm là $10^7$ trong khi phương trình vô nghiệm
Nếu nghiệm dò tìm được có dạng $a \times 10^n$ với $a \in R^*, n \in N^*$ thì cần kiểm tra lại bằng phương thức tính toán Table
Bước 1 Nhập vế trái của phương trình $\sqrt{x^2+4x+1}-(x+2)$
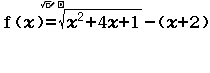
Bước 2 Nhập $Start=10^7-14, End=10^7+14, Step=1$

Bước 3 Nhấn phím =
Qua sát bảng giá trị ta thấy tất cả các giá trị của $x$ đều làm cho $f(x)$ bằng $0$ nên $10^7$ không là nghiệm của phương trình đã cho
Không nên sử dụng tính năng CALC để kiểm tra vì tính năng này cũng ngáo sửu trong trường hợp này
1.1.3 Hiểu sai tính năng của phím bấm
Tính giá trị của biểu thức $\dfrac{1}{\tan(15)}$

Vậy giá trị cần tìm là $\quicklatex{color=”#cf2e2e”} \approx 86.18592517$
Kết luận trên là SAI vì phím $\tan^{-1}$ là hàm lượng giác ngược $\arctan$ chứ không phải nghịch đảo của hàm lượng giác $\tan$
Tương tự $\sin^{-1}, \cos^{-1}$ lần lượt là các hàm lượng giác ngược $\arcsin, \arccos$ chứ không phải là nghịch đảo của các hàm lượng giác $\sin, \cos$
Vậy giá trị cần tìm là $2+\sqrt{3}$
Giải phương trình lượng giác $\tan x =2-\sqrt{3}$
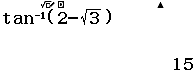
Vậy nghiệm của phương trình là $x=15+k180$ với $k \in Z$
| nPr | Chỉnh hợp |
| nCr | Tổ hợp |
| GCD | Ước chung lớn nhất |
| LCM | Bội chung nhỏ nhất |
| Pol | Chuyển sang toạ độ cực |
| Rec | Chuyển sang toạ chữ nhật |
| Int | Số nguyên của giá trị |
| Intg | Số nguyên lớn nhất không vượt quá giá trị (hàm phần nguyên) |
Cố gắng nhớ kĩ ý nghĩa của các phím bấm, nếu quên bạn có thể thử với các giá trị đơn giản, các giá trị mà bạn đã biết trước kết quả
Phân biệt tính năng của phím bấm GCD và LCM
Dễ thấy $2,3$ có ước chung lớn nhất là $1$
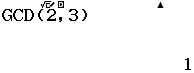
Vậy tính năng của phím bấm GCD là tìm ước chung lớn nhất và LCM là tìm bội chung nhỏ nhất
1.2 Tính toán ma trận
1.2.1 Tính năng Identity
Tính năng Identity cho phép tạo ma trận đơn vị cấp $1, 2, 3 ,4$
Tạo ma trận đơn vị cấp $4 \times 4$
Để tìm ma trận đơn vị cấp $4 \times 4$ bạn hãy chọn Identity rồi nhập cấp của ma trận chứ không phải chọn ma trận
1.2.2 Ma trận bình phương, lập phương và nghịch đảo
Cho ma trận $A=\left[\begin{array}{cccc} 2&9&5&2\\ 0&6&6&6\\ 0&1&8&3\\ 5&0&3&4 \end{array} \right]$ tìm ma trận $A^2$
Để tìm ma trận $A^2$ bạn hãy nhấn phím $x^2$ chứ không phải nhấn phím $x^{\square}$ rồi nhấn phím $2$
Tổng quát để tìm ma trận bình phương, ma trận lập phương, ma trận nghịch đảo chúng ta lần lượt nhấn các phím $x^2, x^3, x^{-1}$
1.3 Tính toán véctơ
Tính tích vô hướng và tích của hướng của $\vec{a}=(8, 1, 7), \vec{b}=(7, 7, 7)$
Bước 1 Định nghĩa $VctA=\vec{a}, VctB=\vec{b}$
Bước 2 Tính tích vô hướng $\vec{a} \cdot \vec{b}$
Bước 3 Tính tích có hướng $[\vec{a}, \vec{b}]$
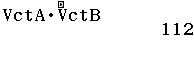
Vậy tích vô hướng và tích có hướng của $\quicklatex{color=”#cf2e2e”} \vec{a}$ và $\quicklatex{color=”#cf2e2e”} \vec{b}$ lần lượt là $\quicklatex{color=”#cf2e2e”} (-42, -7, 49)$ và $\quicklatex{color=”#cf2e2e”} 112$
Kết luận trên là SAI vì tích vô hướng là một số, tích có hướng là một véctơ
Nhầm lẫn giữa tính năng tính tích vô hướng và phím bấm tích có hướng
- Tính năng Dot Product cho phép tính tích vô hướng của hai véctơ
- Phím bấm $\times$ trong phương thức tính toán Vector cho phép tính tích có hướng của hai véctơ
1.4 Tính toán thống kê
1.4.1 Phương sai và độ lệch chuẩn
Máy tính CASIO fx-580VN X cung cấp cho chúng ta hai phương sai và hai độ lệch chuẩn
- $\sigma^2_x$ phương sai
- $\sigma_x$ độ lệch chuẩn
- $s^2_x$ phương sai
- $s_x$ độ lệch chuẩn
Tùy thuộc yêu cầu cụ thể khi tính toán thống kê mà chúng ta sẽ lựa chọn sử dụng cho phù hợp
Phương sai và độ lệnh giống như định nghĩa trong sách giáo khoa Đại số 10 là $\sigma^2_x$, $\sigma_x$
$$\sigma^2_x=\sqrt{\dfrac{\sum(x-\bar{x})^2}{n}}, \sigma_x=\dfrac{\sum(x-\bar{x})^2}{n}$$
1.4.2 Biến đôi $\quicklatex{color=”#00d084″} (x, y)$ hồi quy tuyến tính
Khi xử lí số liệu thống kê tìm phương trình hồi quy tuyến tính thực nghiệm của $y$ theo $x$ là $y=ax+b$, chúng ta thường hay nhầm lẫn hệ số $a$ là $A$ và hệ số $b$ là $B$
Phương trình hồi quy tuyến tính trên máy tính CASIO fx-580VN X có dạng $y=A+Bx$ do đó giá trị của hệ số $a$ là giá trị của $B$ và giá trị của hệ số $b$ là giá trị của $A$
2 Sai lầm khi thiết lập đơn vị góc
Máy tính CASIO fx-580VN X hỗ trợ ba loại đơn vị góc là Degree – Độ, Radian – Ra đi an, Gradian – Gra di an
Quan sát chỉ báo trên màn hình chúng ta dễ dàng biết được máy tính đang thiết lập đơn vị góc nào
 |  |  |
| Degree | Radian | Gradian |
Tùy thuộc vào từng bài toán cụ thể mà chúng ta sẽ thiết lập đơn vị góc cho phù hợp
$\sin(90)$ thì thiết lập đơn vị góc là Degree, $\int_0^\pi sin(x) dx$ hoặc $\dfrac{d}{dx}(\sin(x))|_{x=\pi}$ thì thiết lập đơn vị góc là Radian
3 Sai lầm khác
3.1 Mua nhầm máy tính giả
Sai lầm này có lẽ là sai lầm nghiêm trọng nhất cũng như tốn kèm nhất
- Các linh kiện cấu thành bo mạch có chất lượng thấp, hư hỏng bất cứ lúc nào
- Tốc độ xử lí chậm
- Hoạt động không ổn định
- Chương trình được lập trình một cách cấu thả dẫn đến dễ sai số trong quá trình tính toán
Giải pháp đơn giản nhất và hữu hiệu nhất là chọn nhà cung cấp uy tính
Hiện tại có nhiều nhà cung cấp uy tính, mình xin giới thiệu đến các bạn hai nhà cung cấp uy tính là TIKI và BITEXSHOP
- Ưu điểm của TIKI là giá cả cạnh tranh
- Ưu điểm của BITEXSHOP là thời gian bảo hành
3.2 Mua pin có chất lượng kém
Pin mà máy tính CASIO fx-580VN X sử dụng là pin AAA R03, bạn nên tìm mua chính xác loại pin này
Nếu mua nhằm pin chất lượng kém thì thời gian sử dụng giảm, hết pin bất cứ lúc nào, thậm chí gây hư hỏng bo mạch
3.3 Không gắn lại nắp gài
Bất cứ khi nào, lúc sử dụng cũng như lúc không sử dụng chúng ta đều nên gắn lại nắp gài
Nắp gài này được thiết kế đặc biệt giảm thiểu khả năng hư hỏng nếu lỡ làm rơi hoặc bị chèn ép khi để trong cặp
3.4 Không tháo pin khi không sử dụng trong thời gian dài
Cho dù máy tính vẫn hoạt động bình thường chúng ta cũng cần thay pin ít nhất hai năm một lần