Giải phương trình bậc năm bằng CASIO fx 880 BTG

Xin chào tất cả các bạn

Hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước giải phương trình bậc năm bằng máy tính cầm tay CASIO fx 880 BTG

Như các bạn đã biết, không có phương pháp tổng quát để giải phương trình bậc năm, thông thường chúng ta sẽ

• Cố gắng tìm ra một nghiệm nguyên hoặc nghiệm hữu tỉ
• Sau đó sử dụng sơ đồ Hoocne phân tích phương trình đã cho thành phương trình tích (một bậc nhất và một bậc bốn)

Lý thuyết là như vậy nhưng không phải phương trình bậc năm nào cũng có nghiệm nguyên hoặc nghiệm hữu tỉ

Ngoài ra việc giải phương trình bậc bốn không phải lúc nào cũng dễ dàng, mặc dù đã có phương pháp giải tổng quát

Tóm lại, trong phạm vi ngắn gọn của bài viết chúng ta chỉ tìm hiểu cách sử dụng máy tính cầm tay CASIO fx 880 BTG giải một số phương trình bậc năm mà thôi

1 Các bước giải phương trình

Bước 1 sử dụng tính năng Solver tìm ra một nghiệm của phương trình

Nếu nghiệm tìm được không là nghiệm nguyên thì gán nghiệm vào một biến nhớ bất kỳ

Xem thêm SHIFT SOLVE nghiệm của phương trình

Bước 2 sử dụng kết hợp bộ nhớ trả lời Ans, biến nhớ x và tính năng CALC biến đổi phương trình bậc năm thành phương trình tích (một bậc nhất, một bậc bốn)

Xem thêm Chia sơ đồ Hoocne

Bước 3 sử dụng tính năng Polynomial giải phương trình bậc bốn

Xem thêm Giải phương trình bậc bốn

2 Thực hành giải phương trình

Chẳng hạn mình cần giải phương trình bậc năm $12\,{x}^{5}+28\,{x}^{4}+15\,{x}^{3}+10\,{x}^{2}+3\,x-18$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 sử dụng tính năng Solver tìm ra một nghiệm của phương trình

Bước 1.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

Bước 1.2 nhập $12\,{x}^{5}+28\,{x}^{4}+15\,{x}^{3}+10\,{x}^{2}+3\,x-18$ => nhấn phím EXE => nhấn phím  => nhấn phím EXE

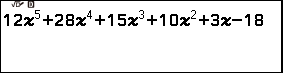
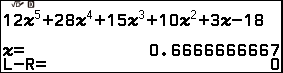
Bước 1.3 nhấn phím VARIABLE => nhấn phím OK => nhấn phím OK (gán nghiệm vừa tìm được vào biến nhớ A)

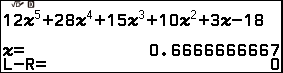
Bước 2 sử dụng kết hợp bộ nhớ trả lời Ans, biến nhớ và tính năng CALC biến đổi phương trình bậc năm thành phương trình tích (một bậc nhất, một bậc bốn)

Bước 2.1 nhấn phím HOME => chọn Calculate => nhấn phím OK

Bước 2.2 chia đa thức $12\,{x}^{5}+28\,{x}^{4}+15\,{x}^{3}+10\,{x}^{2}+3\,x-18$ cho đa thức $x-A$

Bước 2.2.1 nhập 12 => nhấn phím EXE

Bước 2.2.2 nhập $A \times Ans+x$

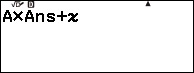
Bước 2.2.3

Nhấn phím TOOLS => nhấn phím OK => nhấn phím  => nhập 28 => nhấn phím OK => nhấn phím OK

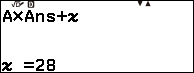
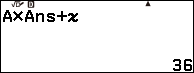
Nhấn phím TOOLS => nhấn phím OK => nhấn phím  => nhập 15 => nhấn phím OK => nhấn phím OK

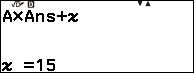
Nhấn phím TOOLS => nhấn phím OK => nhấn phím  => nhập 10 => nhấn phím OK => nhấn phím OK

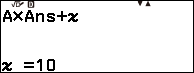
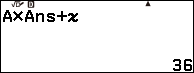
Nhấn phím TOOLS => nhấn phím OK => nhấn phím  => nhập 3 => nhấn phím OK => nhấn phím OK

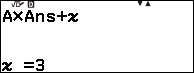
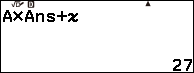
Nhấn phím TOOLS => nhấn phím OK => nhấn phím  => nhập -18 => nhấn phím OK => nhấn phím OK

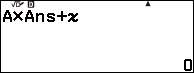
Suy ra đa thức thương và số dư cần tìm lần lượt là $12\,{x}^{4}+36\,{x}^{3}+39\,{x}^{2}+36\,x+27$ và $0$

Suy ra $12\,{x}^{5}+28\,{x}^{4}+15\,{x}^{3}+10\,{x}^{2}+3\,x-18=(x-A)(12\,{x}^{4}+36\,{x}^{3}+39\,{x}^{2}+36\,x+27)$

Để xem lại giá trị của biến nhớ A bạn hãy nhấn phím VARIABLE => nhấn phím OK => nhấn phím OK => nhấn phím OK

Bước 3 sử dụng tính năng Polynomial giải phương trình bậc bốn

Bước 3.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^4+bx^3+cx^2+dx+e$ => nhấn phím OK

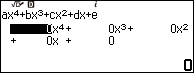
Bước 3.2 nhập các hệ số của phương trình bậc bốn

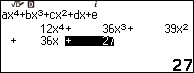
Bước 3.3 nhấn phím EXE

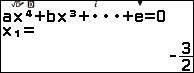
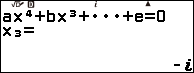
Vậy phương trình bậc năm đã cho có các nghiệm là $\frac{2}{3}, -\frac{3}{2}$ (nghiệm kép), $i, -i$

Nếu bạn đã cài đặt Off / Tắt nghiệm phức khi giải phương trình thì khi nhấn phím EXE máy tính cầm tay CASIO fx 880 BTG chỉ hiển thị nghiệm $-\frac{3}{2}$

Khi giải phương trình bậc bốn bằng máy tính cầm tay CASIO fx 880 BTG nếu thu được một nghiệm thực và hai nghiệm phức liên hợp thì nghiệm thực đó chắn chắn là nghiệm kép

https://youtu.be/AunYYF1y-TE

3 Lời kết

Trong thực hành không phải bao giờ việc giải phương trình bậc năm bằng máy tính cầm tay CASIO fx 880 BTG cũng thuận lợi như vậy

Có một số trường hợp …

• Việc chuyển nghiệm tìm được bằng tính năng Solver sang phân số căn thức khá phức tạp
• Việc chuyển nghiệm tìm được bằng tính năng Polynomial sang căn thức đôi khi cũng khá phức tạp

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo