Cách bấm máy tính CASIO fx 880 BTG tính phân phối chuẩn tắc
Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn tính nhanh phân phối chuẩn bằng máy tính cầm tay CASIO fx 880 BTG
Chúng ta sẽ tính phân phối chuẩn nhớ vào tính năng Norm Dist của ứng dụng tính toán thống Statistics
Từ đây về sau chúng ta không cần phải tra bảng giá trị của hàm LAPLACE ![]() nữa
nữa
1 Sơ lược vế tính năng phân phối chuẩn
Các hàm ![]() lấy đối số
lấy đối số ![]() và xác định xác suất phân phối chuẩn như hình minh họa
và xác định xác suất phân phối chuẩn như hình minh họa
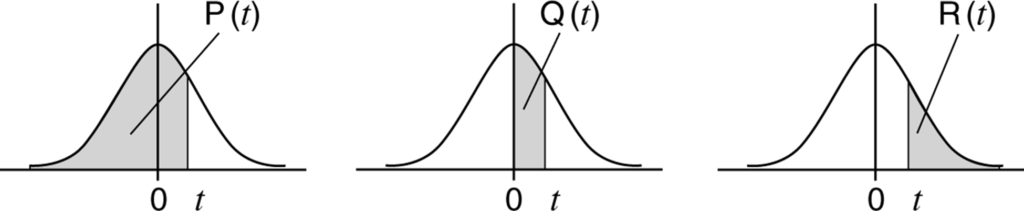
Hàm ![]() có đối số
có đối số ![]() đứng trước
đứng trước
Hàm ![]() tính toán đại lượng ngẫu nhiên chuẩn cho giá trị dữ liệu
tính toán đại lượng ngẫu nhiên chuẩn cho giá trị dữ liệu ![]() sử dụng giá trị trung bình
sử dụng giá trị trung bình ![]() và độ lệch chuẩn không gian mẫu
và độ lệch chuẩn không gian mẫu ![]() của dữ liệu thống kê đã nhập
của dữ liệu thống kê đã nhập
![]()
2 Thực hành tính phân phối
Trọng lượng của một sản phẩm ![]() có phân phối chuẩn với
có phân phối chuẩn với ![]()
Tính tỉ lệ những sản phẩm có trọng lượng từ ![]() đến
đến ![]()
Dễ thấy ![]()
![]()
![]()
![]()
![]()
Bước 1
Nhấn phím HOME => chọn Statistics => nhấn phím OK => chọn 1-Variable => nhấn phím OK => nhấn phím EXE => chọn Statistics Calc => nhấn phím OK




Bước 2
Nhấn phím CATALOG => chọn Statistics => nhấn phím OK => chọn Norm Dist => nhấn phím OK => chọn Q( => nhấn phím OK



Nhập 2 => nhấn phím ) => nhấn phím +

Nhấn phím CATALOG => chọn Statistics => nhấn phím OK => chọn Norm Dist => nhấn phím OK => chọn Q( => nhấn phím OK


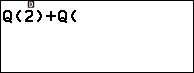
Nhập 1 => nhấn phím )
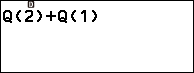
Bước 3 nhấn phím EXE
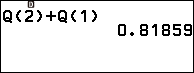
Vậy tỉ lệ những sản phẩm có trọng lượng từ ![]() đến
đến ![]() là
là ![]()
3 Lời kết
Ứng dụng Statistics của máy tính cầm tay CASIO fx 880 BTG ngoài hỗ trợ chúng tính nhanh phân phối chuẩn còn hỗ trợ …
- Thống kê biến đơn (số đặc trưng đo xu thế trung tâm và đo độ phân tán)
- Viết phương trình hồi quy tuyến tính y=ax+b
- Thống kê biến đôi
- …
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
