Phương trình có dạng $Ax+By+Cz+D=0$ với $A^2+B^2+C^2 > 0$ $(A, B, C$ không đồng thời bằng $0)$ được gọi là phương trình tổng quát của mặt phẳng
Về phương diện vị trí, hai mặt phẳng có ba vị trí tương đối là trùng nhau, song song và cắt nhau. Riêng trong trường hợp cắt nhau thì có một trường hợp đặc biệt là vuông góc
Việc xét vị trí tương đối của hai mặt phẳng không có gì khó khăn. Tuy nhiên để rút ngắn thời gian và đảm bảo sự chính xác chúng ta có thể sử dụng phương thức tính toán Verify trong máy tính CASIO fx-580VN X để hỗ trợ

1 Vị trí tương đối của hai mặt phẳng
Trong không gian $Oxyz$ cho hai mặt phẳng $(\alpha)$ và $(\alpha’)$ có phương trình lần lượt là $Ax+By+Cz+D=0$ và $A’x+B’y+C’z+D’=0$
Khi đó
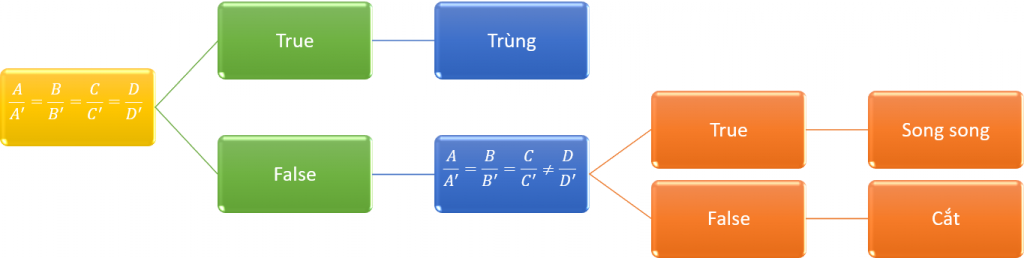
- $(\alpha)$ trùng $(\alpha’) \Leftrightarrow \dfrac{A}{A’}=\dfrac{B}{B’}=\dfrac{C}{C’}=\dfrac{D}{D’}$
- $(\alpha)$ song song $(\alpha’) \Leftrightarrow \dfrac{A}{A’}=\dfrac{B}{B’}=\dfrac{C}{C’}\neq\dfrac{D}{D’}$
- $(\alpha)$ cắt $(\alpha’) \Leftrightarrow (A:B:C) \neq (A’:B’:C’)$
- Nếu $(\alpha)$ và $(\alpha’)$ cắt nhau thì sẽ cắt theo một đường thẳng và phương trình của đường thẳng này là $\left\{\begin{array}{lllll} Ax&+By&+Cz&+D&=0\\A’x&+B’y&+C’z&+D’&=0\end{array}\right.$
- Phương trình trên được gọi là phương trình tổng quát của đường thẳng trong không gian
- Nếu $AA’+BB’+CC’=0$ thì $(\alpha)$ vuông góc $(\alpha’)$
2 Thủ thuật xét vị trí tương đối của hai mặt phẳng
Bước 1 Chọn phương thức tính toán Verify
Bước 2 Nhập biểu thức $\dfrac{A}{A’}=\dfrac{B}{B’}=\dfrac{C}{C’}=\dfrac{D}{D’}$
Dấu = trong biểu thức trên được nhập vào bằng cách nhấn phím OPTN rồi nhấn phím 1
Bước 3 Nhấn phím =
- Nếu máy thông báo True thì kết luận mặt phẳng $(\alpha)$ trùng với mặt phẳng $(\alpha’)$
- Nếu máy thông báo False thì thực hiện Bước 4
Bước 4 Nhập biểu thức $\dfrac{A}{A’}=\dfrac{B}{B’}=\dfrac{C}{C’}\neq\dfrac{D}{D’}$
Dấu $\neq$ trong biểu thức trên được nhập vào bằng cách nhấn phím OPTN rồi nhấn phím 2
Bước 5 Nhấn phím =
- Nếu máy thông báo True thì kết luận mặt phẳng $(\alpha)$ song song với mặt phẳng $(\alpha’)$
- Nếu máy thông báo False thì kết luận mặt phẳng $(\alpha)$ cắt mặt phẳng $(\alpha’)$
3 Ví dụ minh họa
Trong không gian $Oxyz$ cho mặt phẳng $(P): 6x+8y+9z+8=0$ và mặt phẳng $(Q): 36x+48y+54z+48=0$
Vị trí tương đối của hai mặt phẳng này là?

Bước 1 Chọn phương thức tính toán Verify
Bước 2 Nhập biểu thức $\dfrac{6}{36}=\dfrac{8}{48}=\dfrac{9}{54}=\dfrac{8}{48}$
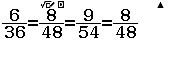
Bước 3 Nhấn phím =
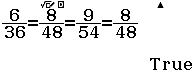
Vậy mặt phẳng $(P)$ trùng với mặt phẳng $(Q)$
Trong không gian $Oxyz$ cho mặt phẳng $(P): 7x+9y+3z+7=0$ và mặt phẳng $(Q): 14x+18y+6z+9=0$
Vị trí tương đối của hai mặt phẳng này là?

Bước 1 Chọn phương thức tính toán Verify
Bước 2 Nhập biểu thức $\dfrac{7}{14}=\dfrac{9}{18}=\dfrac{3}{6}=\dfrac{7}{9}$
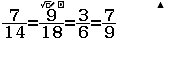
Bước 3 Nhấn phím =
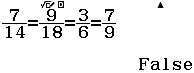
Suy ra mặt phẳng $(P)$ và mặt phẳng $(Q)$ chỉ có thể song song hoặc cắt nhau
Bước 4 Nhập biểu thức $\dfrac{7}{14}=\dfrac{9}{18}=\dfrac{3}{6}\neq\dfrac{7}{9}$
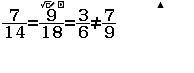
Bước 5 Nhấn phím =
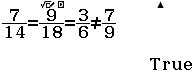
Vậy mặt phẳng $(P)$ song song với mặt phẳng $(Q)$
Trong không gian $Oxyz$ cho mặt phẳng $(P): 8x+2y+6z+8=0$ và mặt phẳng $(Q):4x+4y+9z+3=0$
Vị trí tương đối của hai mặt phẳng này là?
Bước 1 Chọn phương thức tính toán Verify
Bước 2 Nhập biểu thức $\dfrac{8}{4}=\dfrac{2}{4}=\dfrac{6}{9}=\dfrac{8}{3}$
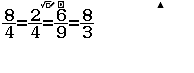
Bước 3 Nhấn phím =
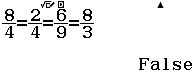
Suy ra mặt phẳng $(P)$ và mặt phẳng $(Q)$ chỉ có thể song song hoặc cắt nhau
Bước 4 Nhập biểu thức $\dfrac{8}{4}=\dfrac{2}{4}=\dfrac{6}{9}\neq\dfrac{8}{3}$
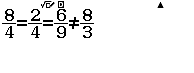
Bước 5 Nhấn phím =
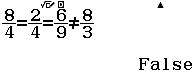
Vậy mặt phẳng $(P)$ cắt mặt phẳng $(Q)$
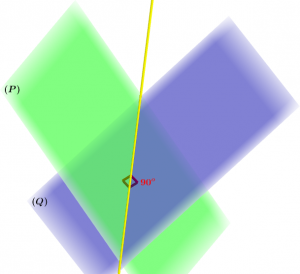
Trong không gian $Oxyz$ cho mặt phẳng $(P): 4x+y+3z+4=0$ và mặt phẳng $(Q):12x+12y-20z+3=0$
Vị trí tương đối của hai mặt phẳng này là?
Bước 1 Chọn phương thức tính toán Verify
Bước 2 Nhập biểu thức $\dfrac{4}{12}=\dfrac{1}{12}=\dfrac{3}{-20}=\dfrac{4}{3}$
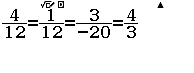
Bước 3 Nhấn phím =
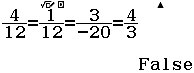
Suy ra mặt phẳng $(P)$ và mặt phẳng $(Q)$ chỉ có thể song song hoặc cắt nhau
Bước 4 Nhập biểu thức $\dfrac{4}{12}=\dfrac{1}{12}=\dfrac{3}{-20}\neq\dfrac{4}{3}$
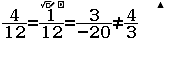
Bước 5 Nhấn phím =
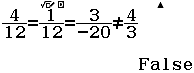
Vậy mặt phẳng $(P)$ cắt mặt phẳng $(Q)$ và đặc biệt hơn nửa chúng còn vuông góc với nhau
Thật vậy $4 \times 12+1 \times 12+3 \times (-20)=0$