Chức năng tính đạo hàm trong máy tính Casio fx-580VN X đã cho phép chúng ta tính đạo hàm của hàm số một biến
Tuy vẫn không được hiển thị dưới dạng tường minh nhưng nếu biết cách kết hợp với phương thức Table chúng ta vẫn giải quyết được các câu tính đạo hàm trong Kỳ thi Trung học Phổ thông Quốc gia

1 Đạo hàm tại một điểm
Phím ![]() cho phép chúng ta tính đạo hàm tại một điểm cho trước
cho phép chúng ta tính đạo hàm tại một điểm cho trước
Khi hàm số có chứa các hàm lượng giác, hàm lượng giác ngược thì bạn nhớ thiết lập Radian làm đơn vị góc mặc định
1.1 Đạo hàm cấp một
Tính $f’(2)$ biết $f(x)=\dfrac{x^2+2x+3}{5x+7}$
Bước 1 Nhấn phím ![]()
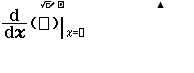
Bước 2 Nhập hàm số => nhập điểm lấy đạo hàm
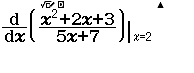
Bước 3 Nhấn phím =
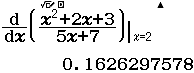
Vậy $f’(2) \approx 0.1626297578$
Tính $f’(\pi)$ biết $f(x)=\sin(2x+3).\cos(5x^2+7x+11)$
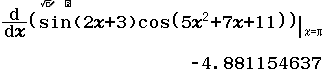
Vậy $f’(\pi) \approx -4.881154637$
1.2 Đạo hàm cấp hai
Máy tính Casio fx-580VN X không hỗ trợ chúng ta tính trực tiếp đạo hàm cấp hai nhưng chúng ta có vẫn thể tính gián tiếp nhờ vào định nghĩa bên dưới
$$f’’(x_0)=\lim_{h \rightarrow 0} \dfrac{f’(x_0+h)-f’(x_0)}{h}$$
Giả sử chúng ta cần tính $f’’(x_0)$
Bước 1 Gán $10^{-9}$ vào biến nhớ A
Bước 2 Tính $f’(A+x_0)$ => gán kết quả vào biến nhớ B
Bước 3 Tính $f’(x_0)$ => gán kết quả vào biến nhớ C
Bước 4 Tính $\dfrac{B-C}{A}$
Phương pháp này chỉ cho ra kết quả gần đúng nhưng với dạng bài kiểm tra/ thi trắc nghiệm thì vẫn sử dụng được
Tính $f’’(2)$ biết $f(x)=\dfrac{x^2+2x+3}{5x+7}$
Bước 1 Gán $10^{-9}$ vào biến nhớ A

Bước 2 Tính $f’(A+2)$ => gán vào biến nhớ B
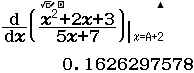

Bước 3 Tính $f’(2)$ => gán vào biến nhớ C
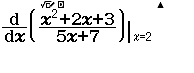

Bước 4 Tính $\dfrac{B-C}{A}$

Vậy $f’’(2) \approx \dfrac{11}{500}$
Tính $f’’(\pi)$ biết $f(x)=\sin(2x+3).\cos(5x^2+7x+11)$

Vậy $f’’(\pi) \approx -73.10934$
3 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia
Tính đạo hàm của hàm số h(x) với các phương án A, B, C, D cho trước
Bước 1 Thiết lập sử dụng cả hàm f(x) và hàm g(x)
Bước 2 Chọn phương thức Table
Bước 3 Nhập f(x) là đạo hàm của h(x) trừ hàm số ở phương án A
Bước 4 Nhập g(x) là đạo hàm của h(x) trừ hàm số ở phương án B
Bước 5 Nhập Start=1, End=30 và Step=1
Bước 6 Quan sát bảng giá trị
- Nếu có hàm số nào bằng không hoặc gần bằng không thì chọn phương án tương ứng
- Nếu không có thì nhấn phím AC, rồi thực hiện lại Bước 3, 4 cho phương án C và D
Hàm số $y=\log _{2} \sqrt{x^{2}+x}$ có đạo hàm là hàm
A. $y’=\dfrac{2 x+1}{(x^{2}+x)}$
B. $y’=\dfrac{2 x+1}{2(x^{2}+x) \ln 2}$
C. $y’=\dfrac{2 x+1}{(x^{2}+x) \ln 2}$
D. $y’=\dfrac{(2 x+1) \ln 2}{2(x^{2}+x)}$
Bước 1 Nhập hàm f(x)
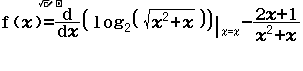
Bước 2 Nhập hàm g(x)
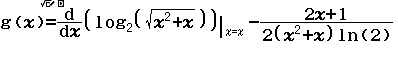
Bước 3 Nhập Start = 1, End = 30, Step = 1
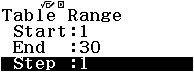
Bước 4 Nhấn phím =
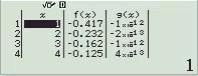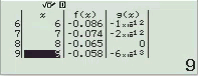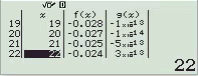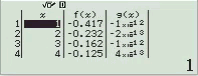
Quan sát bảng giá trị ta thấy giá trị của hàm g(x) tiệm cận 0. Vậy B là đáp án
Đạo hàm của hàm số $y=2^x$ là
A. $y’=2^x \ln 2$
B. $y’=2^x$
C. $y’=\dfrac{2^x}{\ln 2}$
D. $y’=x2^{x-1}$
Bước 1 Nhập hàm f(x)
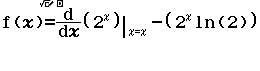
Bước 2 Nhập hàm g(x)
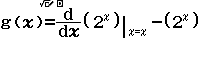
Bước 3 Nhập Start = 1, End = 30, Step = 1

Bước 4 Nhấn phím =
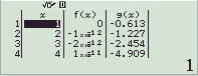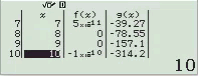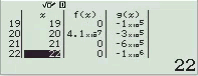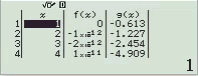
Quan sát bảng giá trị ta thấy giá trị của hàm f(x) tiệm cận 0. Vậy A là đáp án
Hàm số $y=2^{x^2-3x}$ có đạo hàm là
A. $(2x-3).2^{x^2-3x}.\ln 2$
B. $2^{x^2-3x}.\ln 2$
C. $(2x-3).2^{x^2-3x}$
D. $(x^2-3x).2^{x^2-3x-1}$
Bước 1 Nhập hàm f(x)
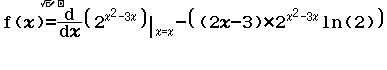
Bước 2 Nhập hàm g(x)
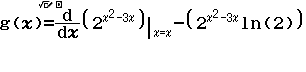
Bước 3 Nhập Start = 1, End = 30, Step = 1

Bước 4 Nhấn phím =
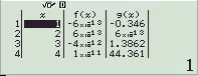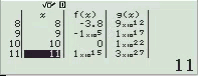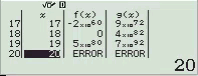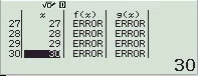
Quan sát bảng giá trị ta thấy giá trị của hàm f(x) tiệm cận 0. Vậy A là đáp án


