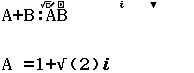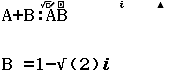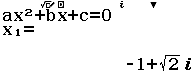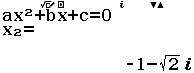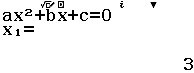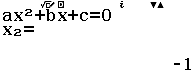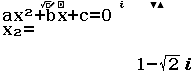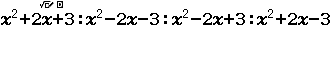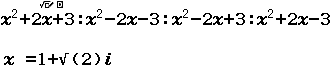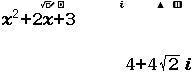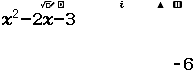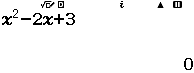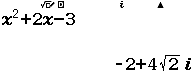Tích phân không xác định (nguyên hàm) không thể tính trực tiếp bằng máy tính Casio fx-580VN X nhưng tích phân xác định (tích phân) có thể tính được một cách dễ dàng
Ở đây mình sẽ hướng dẫn các bạn chi tiết cách tính tích phân của một hàm số bất kì. Đồng thời đề xuất hướng giải quyết khi kết quả là số vô tỉ

1 Trường hợp kết quả là số hữu tỉ
Tích phân $\int_1^2 x^3 dx$ bằng
A. $\dfrac{15}{3}$
B. $\dfrac{17}{4}$
C. $\dfrac{7}{4}$
D. $\dfrac{15}{4}$
Bước 1 Nhập tích phân $\int_1^2 x^3 dx$

Bước 2 Nhấn phím =

Vậy phương án D là đáp án
2 Trường hợp kết quả là số vô tỉ
$\int_1^2 e^{3x-1} dx$ bằng
A. $\dfrac{1}{3}(e^5-e^2)$
B. $\dfrac{1}{3}e^5-e^2$
C. $e^5-e^2$
D. $\dfrac{1}{3}(e^5+e^2)$
Bước 1 Nhập tích phân $\int_1^2 e^{3x-1} dx$
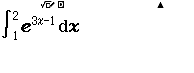
Bước 2 Nhấn phím =
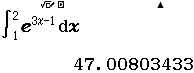
Bước 3 Chuyển các giá trị ở bốn phương án sang dạng hiển thị thập phân
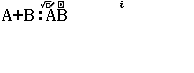
$\dfrac{1}{3}(e^5-e^2):\dfrac{1}{3}e^5-e^2:e^5-e^2:\dfrac{1}{3}(e^5+e^2)$
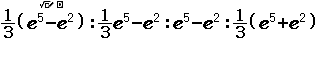
Bước 4 Nhấn phím =
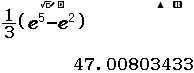


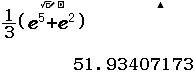
Vậy phương án A là đáp án
3 Trường hợp không yêu cầu tính giá trị của tích phân
Trường hợp không yêu cầu tính giá trị của tích phân thường nhằm hướng thí sinh giải bằng hình thức tự luận
Tuy nhiên nếu gặp các hàm dưới dấu tích phân phức tạp thì việc biến đổi sơ cấp (giải) sẽ tồn nhiều thời gian và công sức
Trong một số trường hợp chúng ta vẫn có thể sử dụng máy tính Casio fx-580VN X để hỗ trợ, rút ngắn thời gian tìm ra kết quả
Trường hợp này có rất nhiều dạng toán khác nhau nhưng mình chỉ trình bày thuật giải của dạng thường gặp nhất
Thiết lập chỉ sử dụng duy nhất hàm f(x) trước khi thực hiện thuật giải
Cho $\int_{a}^{b} f(x) d x=a_{1} \ln x_{1}+a_{2} \ln x_{2}+\ldots+a_{n} \ln x_{n}$ với $x_{1}, x_{2}, \ldots, x_{n}$ là các giá trị đã biết. Tìm các số hữu tỉ $a_{1}, a_{2}, \ldots, a_{n}$
Bước 1 Biến đổi sơ cấp $\int_{a}^{b} f(x) d x=a_{1} \ln x_{1}+a_{2} \ln x_{2}+\ldots+a_{n} \ln x_{n} \Leftrightarrow e^{\int_{a}^{b} f(x) d x}=x_{1}^{a_{1}} x_{2}^{a_{2}} \ldots x_{n}^{a_{n}}$
Bước 2 Chọn phương thức tính toán Table
Bước 3 Nhập tích phân $e^{x\int_{a}^{b} f(x) d x}$
Bước 4 Nhập $Start=1, End=45, Step=1$
Bước 5 Tìm và ghi nhớ những f(x) có giá trị là số hữu tỉ
Bước 6 Chọn phương thức tính toán Calculate
Bước 7 Sử dụng tính năng FACT phân tích tử số và mẫu số thành thừa số nguyên tố
Bước 8 Biến đổi sơ cấp rồi suy ra các giá trị $a_{1}, a_{2}, \ldots, a_{n}$
Cho $\int_{16}^{55} \frac{dx}{x \sqrt{x+9}}=a \ln 2+ b \ln 5+ c \ln 11$ với $a, b, c$ là các số hữu tỉ. Mệnh đề nào dưới đây là đúng
A. $a-b=-c$
B. $a+b=c$
C. $a+b=3c$
D. $a-b=-3c$
Bước 1 Biến đổi sơ cấp $\int_{16}^{55} \frac{dx}{x \sqrt{x+9}}=a \ln 2+ b \ln 5+ c \ln 11 \Leftrightarrow e^{\int_{16}^{55} \frac{dx}{x \sqrt{x+9}} }=2^a5^b11^c$
Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập tích phân $e^{x \int_{16}^{55} \frac{dx}{x \sqrt{x+9}}}$
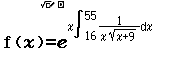
Bước 4 Nhập $Start=1, End=45, Step=1$
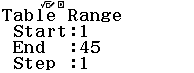
Bước 5 Tìm và ghi nhớ những f(x) có giá trị là số hữu tỉ
Quan sát bảng giá trị chúng ta nhận thấy $f(3)=1.818181818=\dfrac{20}{11}$
 |  |
Bước 6 Chọn phương thức tính toán Calculate

Bước 7 Sử dụng tính năng FACT phân tích tử số và mẫu số thành thừa số nguyên tố


Suy ra $\dfrac{20}{11}=\dfrac{2^25^1}{11^1}$
Bước 8 Biến đổi sơ cấp rồi suy ra các giá trị $a_{1}, a_{2}, \ldots, a_{n}$
Vì $f(3)=\dfrac{20}{11}=\dfrac{2^25^1}{11^1}=2^25^111^{-1}$ nên $a=\dfrac{2}{3}, b=\dfrac{1}{3}, c=\dfrac{-1}{3}$
Vậy phương án A là đáp án
4 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia
$\int_0^\pi \sin(x) + \cos(x) dx$ bằng
A. $1$
B. $2$
C. $-2$
D. $1$
Bước 1 Nhập tích phân
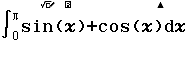
Bước 2 Nhấn phím =
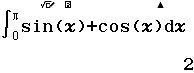
Vậy phương án B là đáp án
$\int_{0}^{1} e^{3 x+1} dx$ bằng
A. $\dfrac{1}{3}\left(e^{4}-e\right)$
B. $e^{4}-e$
C. $\dfrac{1}{3}\left(e^{4}+e\right)$
D. $e^{3}-e$
Bước 1 Tính tích phân $\int_0^1 e^{3x+1} dx$

Bước 2 Chuyển đổi dạng thức hiển thị

Vậy phương án A là đáp án
Cho $\int_{5}^{21} \frac{dx}{x \sqrt{x+4}}=a \ln 3+b \ln 5+c \ln 7$ với $a, b, c$ là các số hữu tỉ. Mệnh đề nào dưới đây đúng
A. $a+b=-2 c$
B. $a+b=c$
C. $a-b=-c$
D. $a-b=-2 c$
$\int_{5}^{21} \frac{dx}{x \sqrt{x+4}}=\frac{1}{2} \ln \left(\frac{15}{7}\right)= \frac{1}{2} \ln (3)+ \frac{1}{2} \ln (5)- \frac{1}{2}\ln (7)$
Vì $a=\frac{1}{2}, b=\frac{1}{2}, c=\frac{-1}{2}$ nên $a+b=-2 c$
Vậy phương án A là đáp án
Thuật giải vừa giới thiệu là thuật giải không hoàn toàn. Tức có một số bài cho dù rơi vào đúng dạng vẫn không giải được. Đây là một trong những nhược điểm “chết người” của các thủ thuật Casio
Tuy nhiên nhược điểm này chỉ gặp với các thủ thuật nâng cao, còn các thủ thuật cơ bản thì hầu như không bị