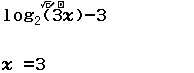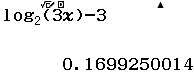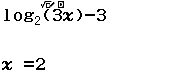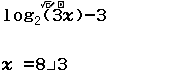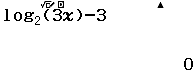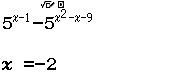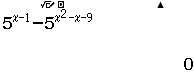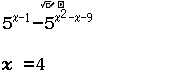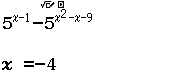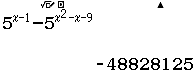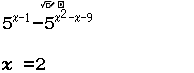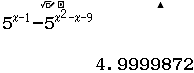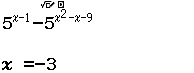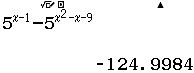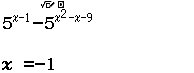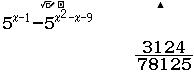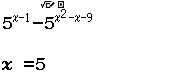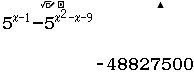Thứ Ba, Tháng Tư 16, 2024

Kỳ thi THPT Quốc gia

Giải phương trình mũ, phương trình logarit bằng máy tính Casio fx-580VN X

23/06/202123/06/2021Nhut Nguyen Minh

Bài này thuộc phần 9 trong 12 phần của series Ứng dụng máy tính Casio fx-580VN X trong Kỳ thi THPT Quốc gia

Như chúng ta đã biết tính năng SOLVE cho phép dò tìm nghiệm của một phương trình bất kì

Tuy nhiên do những hạn chế của tính năng này mà việc do tìm nghiệm của phương trình mũ, phương trình logarit không phải bao giờ cũng diễn ra như ý

Mặc khác chúng ta đã có bốn phương án cho trước nên thay vì tìm chúng ta nên thử

Mục lục nội dung

1 Giải phương trình mũ, phương trình logarit

1.1 Sử dụng phương thức tính toán Table

Câu 12, Đề thi tham khảo, Năm 2021

Nghiệm của phương trình $5^{2x-4}=25$ là

A. $x=3$

B. $x=2$

C. $x=1$

D. $x=-1$

Bước 1 Biến đổi phương trình sao cho vế phải bằng $0$

$5^{2x-4}=25 \Leftrightarrow 5^{2x-4}-25=0$

Bước 2 Chọn phương thức tính toán Table

Bước 3 Nhập vế trái của phương trình

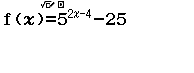
Bước 4 Nhập Start = “giá trị nhỏ nhất”, End = “giá trị lớn nhất”, Step = 1

Chú ý 1.1

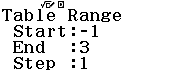
Giá trị nhỏ nhất, lớn nhất lấy từ các giá trị ở bốn phương án

Bước 5 Quan sát bảng giá trị của f(x)

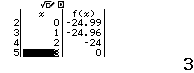
$f(3)=0$ nên $3$ là nghiệm của phương trình đã cho

1.2 Sử dụng tính năng CALC

Câu 13, Đề thi tham khảo, Năm 2021

Nghiệm của phương trình $\log_2 (3x)=3$ là

A. $x=3$

B. $x=2$

C. $x=\dfrac{8}{3}$

D. $x=\dfrac{1}{2}$

Bước 1 Biến đổi phương trình sao cho vế phải bằng $0$

$\log_2 (3x)=3 \Leftrightarrow \log_2 (3x)-3=0$

Bước 2 Nhập vế trái của phương trình

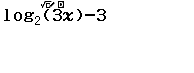
Bước 3 CALC lần lượt bốn giá trị ở bốn phương án

Suy ra $x=3$ không là nghiệm

Suy ra $x=2$ không là nghiệm

Vậy $x=\dfrac{8}{3}$ là nghiệm của phương trình đã cho

Chú ý 1.2

Nếu giá trị ở bốn phương án là các số nguyên thì nên sử dụng phương thức Table
Một số ít trường hợp khi “khoảng cách” giữa giá trị nhỏ nhất và lớn nhất lớn hơn 29 hoặc 45 thì máy tính thông báo Range ERROR. Khi gặp trường hợp này bạn hãy sử dụng tính năng CALC

2 Giải bất phương trình mũ, bất phương trình logarit

Câu 21, Đề thi tham khảo, Năm 2020

Tập nghiệm của bất phương trình $5^{x-1} \geq 5^{x^2-x-9}$ là

A. $[-2; 4]$

B. $[-4; 2]$

C. $(- \infty; -2)\cup[4; + \infty)$

D. $(- \infty; -4)\cup[2; + \infty)$

Bước 1 Biến đổi bất phương trình sao cho vế phải bằng $0$

$5^{x-1} \geq 5^{x^2-x-9} \Leftrightarrow 5^{x-1} - 5^{x^2-x-9} \geq 0$

Bước 2 Tìm tập hợp $A$

Biết tập hợp $A$ là những giá trị mút (không tính $-\infty, +\infty$ ) ở bốn phương án

Suy ra $A=\{-2; 4; -4; 2\}$

Bước 3 Tìm tập hợp $B$

Biết tập hợp $B$ là những phần tử của tập hợp $A$ làm cho vế trái của bất phương trình bằng $0$ hoặc không xác định

Sử dụng tính năng CALC để kiểm tra

Suy ra $-2; 4 \in B$

Suy ra $-4; 2 \notin B$

Vậy $B=\{-2, 4\}$

Chú ý 2

Trong quá trình CALC nếu máy tính thông báo Math ERROR thì đó chính là giá trị không xác định

Bước 4 Lập Bảng và điền các phần tử của B vào (sắp xếp theo thứ tự tăng dần)

Bảng

Bước 5 Tương ứng với mỗi khoảng hãy lấy một giá trị bất kì để xét dấu

Giải sử mình sẽ lấy $-3 \in (-\infty; -2)$ , $-1 \in (-2; 4)$ , $5 \in (4; +\infty)$

Suy ra $(-\infty; -2)$ tương ứng với dấu $-$

Suy ra $(-2; 4)$ tương ứng với dấu $+$

Suy ra $(4; +\infty)$ tương ứng với dấu $-$

Vậy tập nghiệm của bất phương trình đã cho là $[-2; 4]$

Ở đây mình lập bảng là để thuận tiện cho mình hướng dẫn cũng như cho các bạn theo dõi

Khi thành thạo bạn chỉ cần tìm tập hợp B, tương ứng với mỗi khoảng lấy một giá trị, xét dấu giá trị đó

3 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia

Câu 26, Mã đề thi 101, Năm 2019

Nghiệm của phương trình $\log_3 (x+1)+1=\log_3 (4x+1)$ là

A. $x=3$

B. $x=-3$

C. $x=4$

D. $x=2$

Bước 1 Nhập vế trái của phương trình

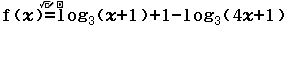
Bước 2 Nhập $Start = -3, End = 4, Step = 1$

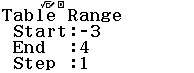
Bước 3 Bảng giá trị của f(x)

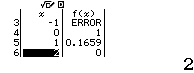
$f(2)=0$ nên $2$ là nghiệm của phương trình đã cho

Câu 17, Mã đề thi 101, Năm 2017

Tập nghiệm $S$ của bất phương trình $\log_2^2x - 5 \log_2 x + 4 \geq 0$

A. $S=(-\infty; 2] \cup [16; + \infty)$

B. $S=[2; 16]$

C. $S=(0; 2] \cup [16; + \infty)$

D. $S=(-\infty; 1] \cup [4; + \infty)$

Bước 1 $\log_2^2 x - 5 \log_2 x + 4 \geq 0$

Bước 2 $A=\{2; 16; 0; 1; 4\}$

Bước 3 $B=\{2; 16; 0\}$

Bước 4

Chú ý 3

Vì tập xác định của hàm số $\log_2^2x - 5 \log_2 x + 4$ là $(0; +\infty)$ nên chúng ta không cần quan tâm đến khoảng $(-\infty; 0)$

Bước 5

Vậy tập nghiệm của bất phương trình đã cho là $S=(0; 2] \cup [16; + \infty)$

Bài viết cùng Serie<< Ứng dụng Casio fx-580VN X giải các dạng toán về hàm số lũy thừa/ mũ/ logaritTính nguyên hàm bằng máy tính Casio fx-580VN X >>

Trả lời Hủy