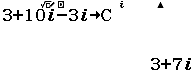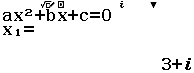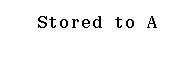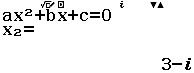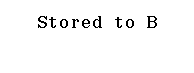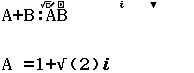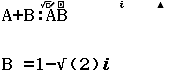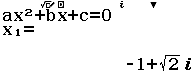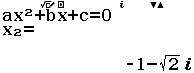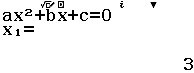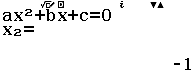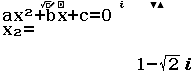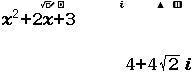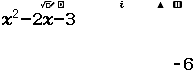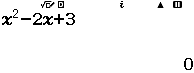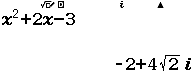- Nhập số phức
- Thực hiện các phép tính (cộng, trừ, nhân, chia, lũy thừa và khai căn)
- Tìm Argument
- Tìm số phức liên hợp
- Tìm phần thực và phần phần ảo
- Chuyển đổi số phức từ dạng đại số sang dạng lượng giác và ngược lại
Tất cả các nội dung trên đều đã được hướng dẫn chi tiết trong Tính toán số phức bằng máy tính Casio fx-580VN X
Ở đây mình chỉ hướng dẫn giải phương trình $az+b \bar{z}=c$ và giải một số dạng toán thường gặp
- Tất cả các thao tác trong bài viết này đều được thực hiện trong phương thức tính toán Complex
- Thao tác nào thực hiện trong phương thức tính toán khác mình sẽ có chỉ dẫn cụ thể
1 Giải phương trình $\quicklatex{color=”00d084″ size=26} az+b \bar{z}=c$
Bước 1 Biến đổi phương trình đã cho về dạng $az+b \bar{z}=c$
Bước 2 Xác định các số phức $a, b, c$ tương ứng
Bước 3 Gán các số phức $a, b, c$ lần lượt vào biến nhớ A, B, C
Bước 4 Nhập biểu thức $\dfrac{CConjg(A)-Conjg(C) B}{|A|^{2}-|B|^{2}}$
- Conjg(A) là số phức liên hợp của A và Conjg(C) là số phức liên hợp của C
- Số phức liên hợp được nhập vào bằng cách nhấn phím OPTN => nhấn phím 2
Cho số phức $z$ thỏa mãn $3(\bar{z}+i)-(2-i)z=3+10i$. Mô-đun của $z$ bằng
A. $3$
B. $5$
C. $\sqrt{5}$
D. $\sqrt{3}$
Bước 1 Biến đổi sơ cấp
$3(\bar{z}+i)-(2-i)z=3+10i \Leftrightarrow -(2-i)z+3 \bar{z}=3+10i-3i$
Bước 2 Gán $-(2-i)$ cho biến nhớ A, $3$ cho biến nhớ B, $3+10i-3i$ biến nhớ C
Bước 3 Nhập biểu thức $\dfrac{CConjg(A)-Conjg(C) B}{|A|^{2}-|B|^{2}}$ => nhấn phím =
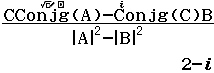
Bước 4 Nhấn phím Abs => nhấn phím Ans => nhấn phím =

Vậy phương án C là đáp án
2 Ứng dụng trong Kỳ thi Trung học Phổ thông Quốc gia
Gọi $z_1, z_2$ là hai nghiệm phức của phương trình $z^2-6z+10=0$. Giá trị của $z_1^2+z_2^2$ bằng
A. $16$
B. $56$
C. $20$
D. $26$
Bước 1 Chọn phương thức tính toán Equation/ Func
Bước 2 Giải phương trình $z^2-6z+10=0$
Bước 3 Lần lượt gán nghiệm $x_1= 3+i$ và $x_2=3-i$ vào biến nhớ A, B
Bước 4 Chọn phương thức tính toán Complex

Bước 5 Nhập biểu thức $A^2+B^2$ => nhấn phím =

Vậy phương án A là đáp án
Tìm hai số thực $x$ và $y$ thỏa mãn $(2x-3yi)+(1-3i)=x+6i$ với $i$ là đơn vị ảo
A. $x=-1; y=-3$
B. $x=-1; y=-1$
C. $x=1; y=-1$
D. $x=1; y=-3$
Bước 1 Biến đổi sơ cấp
$(2x-3yi)+(1-3i)=x+6i \Leftrightarrow (2x-3yi)+(1-3i)-(x+6i)=0$
Bước 2 Nhập vế trái của phương trình $(2x-3yi)+(1-3i)-(x+6i)$
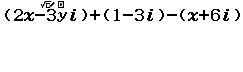
Bước 3 Nhấn phím CALC => nhập $x=-1$ => nhập $y=-3$
Vậy phương án A là đáp án
Phương trình nào dưới đây nhận hai số phức $1+ \sqrt{2}i$ và $1- \sqrt{2}i$ làm nghiệm
A. $z^2+2z+3=0$
B. $z^2-2z-3=0$
C. $z^2-2z+3=0$
D. $z^2+2z-3=0$
Cách 1 Sử dụng định lý Viète
Bước 1 Nhập đa biểu thức $A+B:AB$
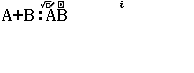
Bước 2 Nhấn phím CALC => nhập $A = 1+ \sqrt{2}i$ => nhập $B = 1- \sqrt{2}i$
Bước 3 Nhấn phím =
Vậy phương án C là đáp án
Cách 2 Giải phương trình
Bước 1 Chọn phương thức tính toán Equation/ Func
Bước 2 Giải phương trình $z^2+2z+3=0$
Suy ra phương án A không là đáp án
Bước 3 Giải phương trình $z^2-2z-3=0$
Suy ra phương án B không là đáp án
Bước 4 Giải phương trình $z^2-2z+3=0$
Vậy phương án C là đáp án
Cách 3 Sử dụng tính năng đa biểu thức và tính năng CALC
Bước 1 Nhập $x^2+2x+3:x^2-2x-3:x^2-2x+3:x^2+2x-3$
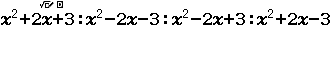
Bước 2 Nhấn phím CALC => nhập $x=A = 1+ \sqrt{2}i$
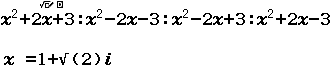
Bước 3 Nhấn phím =
Vậy phương án C là đáp án