Thủ thuật tính đạo hàm cấp hai tại một điểm bằng máy tính cầm tay đã có từ nhiều năm trước
Hôm nay mình sẽ hướng dẫn cho các bạn một thủ thuật mới, cũng là tính đạo hàm cấp hai tại một điểm nhưng thực hiện bằng bảng tính Spreadsheet của máy tính cầm tay CASIO fx 880 BTG
Việc tính đạo hàm cấp hai tại một điểm bằng bảng tính Spreadsheet có nhiều ưu điểm hơn so với thủ thuật truyền thống
1 Các bước thực hiện
Chẳng hạn mình cần tính $f”(2)$ biết $f(x)=\frac{2x-3}{5x^2-7x+11}$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 gán hàm số $f(x)=\frac{2x-3}{5x^2-7x+11}$ vào hàm nhớ f(x)
Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập hàm số $\frac{2x-3}{5x^2-7x+11}$ => nhấn phím OK
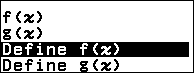
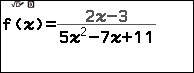
Xem thêm Gán một hàm số bất kì vào hàm nhớ f(x)
Bước 2 mở ứng dụng bảng tính Spreadsheet
Nhấn phím HOME => sử dụng các phím ![]() con trỏ chọn Spreadsheet => nhấn phím OK
con trỏ chọn Spreadsheet => nhấn phím OK

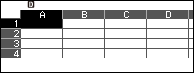
Bước 3 nhập các giá trị
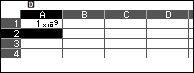
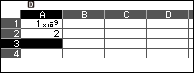
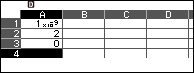
- Nhập $10^{-9}$ vào ô A1 => nhấn phím EXE
- Nhập 2 vào ô A2 => nhấn phím EXE
- Nhập 0 vào ô A3 => nhấn phím EXE
Đôi lời giải thích về các giá trị
- $10^{-9}$ và 0 là bắt buộc phải nhập khi tính đạo hàm cấp hai bằng thủ thuật này
- 2 là điểm cần tính đạo hàm cấp hai
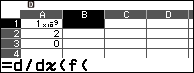
Bước 4 nhập công thức =d/dx(f(x),A1+A2)
Bước 4.1 chọn ô B1 => nhập kí tự đặc biệt =
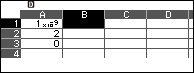
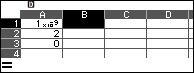
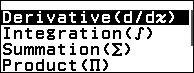
Bước 4.2 nhấn phím CATOLOG => chọn Func Analysis => nhấn phím OK => Derivative => nhấn phím OK

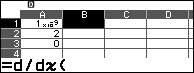
Bước 4.3 nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhấn phím x => nhấn phím ) => nhập , => nhập A1+A2 => nhấn phím EXE

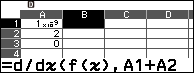
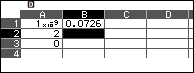
Bước 5 sao chép công thức của ô B1 rồi dán vào ô B2
- Chọn ô B1 => nhấn phím TOOLS => chọn Copy & Paste => nhấn phím OK
- Chọn ô B2 => nhấn phím OK => nhấn phím AC


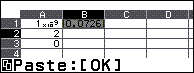
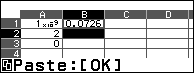
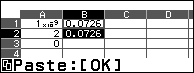
Bước 6 nhập công thức $=(B1-B2) \lrcorner A1$
Chọn C1 => nhập công thức $=(B1-B2) \lrcorner A1$ => nhấn phím EXE



Giá trị của ô C1 chính là giá trị gần đúng của $f’’(2)$
Để hiển thị được nhiều chữ số thập phân hơn bạn hãy nhấn TOOLS => chọn Show Cell => nhấn phím OK => chọn Value => nhấn phím OK => nhấn phím AC



Vậy $f”(2) \approx -0.1457358029$
2 Ưu điểm và nhược điểm của thủ thuật
Bất kì thủ thuật nào cũng có ưu điểm và nhược điểm riêng, thủ thuật này tất nhiên cũng không ngoại lệ
2.1 Ưu điểm
- Có thể tính được đạo hàm cấp hai tại một điểm khác một cách nhanh chóng
- Có thể tính được đạo hàm cấp hai tại một điểm khác của một hàm số khác một cách nhanh chóng
2.2 Nhược điểm
Khó thực hiện nếu bạn chưa biết cách sử dụng bảng tính bảng tính Spreadsheet
Xem thêm Cách sử dụng bảng tính Spreadsheet
3 Khai thác thủ thuật
Khai thác hai ưu điểm trên chúng ta dễ dàng tính được đạo hàm cấp hai tại một điểm khác của cùng một hàm số hoặc khác hàm số
3.1 Tính đạo hàm cấp hai tại một điểm khác (cùng hàm số)
Giả sử mình cần tính $f”(-2)$ biết $f(x)=\frac{2x-3}{5x^2-7x+11}$ thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Chọn ô A2 => nhập -2 => nhấn phím EXE


Vậy $f”(-2) \approx -0.02409876543$
3.2 Tính đạo hàm cấp hai tại một điểm khác (khác hàm số)
Giả sử mình cần tính $f”(-2)$ biết $f(x)=2x^2+3x+5$ thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Bước 1 gán hàm số $2x^2+3x+5$ vào hàm nhớ f(x)
Bước 1.1 nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập hàm số $2x^2+3x+5$=> nhấn phím EXE
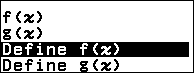
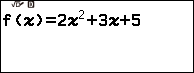
Bước 2 cập nhật lại các giá trị trong bảng tính
Nhấn phím TOOLS => chọn Recalculate => nhấn phím OK

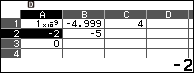

Vậy $f”(-2) \approx 4$
https://youtu.be/d3pA9p74EiU
4 Lời kết
Tuy cách tính đạo hàm cấp hai tại một điểm bằng bảng tính Spreadsheet của máy tính cầm tay CASIO fx 880 BTG chỉ cho ra kết quả gần đúng nhưng nó vẫn có nhiều giá trị trong học tập, kiểm tra và thi cử
- Nếu là tự luận sẽ xác định được kết quả mà chúng ta tính được là đúng hay là sai
- Nếu là trắc nghiệm sẽ khoanh được đáp án
- Hỗ trợ thủ thuật tìm cực trị của một hàm số bất kì
- …
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo