Xin chào tất cả các bạn, hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước tìm các số nguyên a, b, c khi cho biết tích phân bằng máy tính cầm tay CASIO fx 880 BTG
Về cơ bản có chúng ta sẽ sử dụng chức năng tính tích phân Integration và tính năng phân tích thừa số nguyên tố Prime Factor
Trong phạm vi ngắn gọn của bài viết này chúng ta sẽ giải quyết dạng thường gặp nhất là $\int_a^b f(x) dx=a_1\ln x_1+a_2\ln x_2+a_3\ln x_3$
Xem thêm
- Xác định các số nguyên hoặc hữu tỉ a, b khi cho biết tích phân
- Xác định các số hữu tỉ a, b, c khi cho biết tích phân
1 Các bước tìm các số nguyên
Bước 1 sử dụng chức năng tính tích phân Integration giá trị biểu thức $e^{\int_a^b f(x) dx}$
Bước 2 sử dụng tính năng phân tích thừa số nguyên tố Prime Factor phân tích tử số và mẫu số vừa tìm được thành thừa số nguyên tố
Bước 3 dựa vào thừa số nguyên tố vừa phân tích và biểu thức $x_1^{a_1}x_2^{a_2}x_3^{a_3}$ suy ra $a_1, a_2, a_3$
2 Thực hành tìm các số nguyên
Biết $I=\int_3^4 \frac{1}{x^2+x}dx=a\ln 2+b\ln3+c\ln5$ với $a, b, c$ là các số nguyên. Giá trị của biểu thức $a+b+c$ bằng
A. 6
B. 2
C. -2
D. 0
Bước 1 nhấn phím SHIFT => nhấn phím 8 => nhấn phím 
=> nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Integration => nhấn phím OK => nhập $\int_3^4 \frac{1}{x^2+x}dx$ => nhấn phím EXE
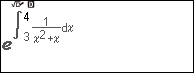
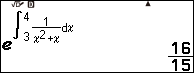
Bước 2
Nhập 16 => nhấn phím EXE => nhấn phím FORMAT => chọn Prime Factor => nhấn phím EXE
Nhập 15 => nhấn phím EXE => nhấn phím FORMAT => chọn Prime Factor => nhấn phím EXE
Bước 3 xác định các số nguyên a, b, c
Dễ thấy $\frac{16}{15}=\frac{2^4}{3.5}=2^4.3^{-1}.5^{-1}=2^a.3^b.5^c$, suy ra $a=4, b=-1, c=-1$
Vậy $a+b+c=2$
https://youtube.com/shorts/P1p4RmzglRU?feature=share
3 Lời kết
Trên đây là chi tiết các bước tìm các số nguyên a, b, c khi cho tích phân bằng máy tính cầm tay CASIO fx 880 BTG
Thao tác khá nhanh và khá đơn giản, nhanh hơn thao tác tìm các số nguyên hoặc các số hữu tỉ a, b khi cho tích phân khá nhiều
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
