Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn chi tiết các bước sử dụng máy tính cầm tay CASIO fx 880 BTG hỗ trợ lập nhanh bảng biến thiên
Việc lập bảng biến thiên bằng máy tính cầm tay cần phải sử dụng khá nhiều tính năng và thủ thuật

1 Các bước lập bảng
Bước 1 tập xác định
- Nếu là hàm đa thức thì tập xác định là R
- Nếu là hàm phân thức thì sử dụng tính năng Solver dò tìm nghiệm của mẫu thức, lúc bấy giờ tập xác định là R hiệu nghiệm vừa tìm được
Bước 2 xét sự biến thiên
Bước 2.1
- Sử dụng tính năng Function tìm giới hạn tại vô cực và giới hạn vô cực (nếu có) của hàm số
- Sử dụng tính năng Function tìm các đường tiệm cận của đồ thị (nếu có)
Bước 2.2 lập bảng biến thiên của hàm số
- Sử dụng kiến thức Toán học và tính năng Equation giải phương trình $y’=0$
- Sử dụng tính năng Function và Derivative xét dấu đạo hàm và xét chiều biến thiên
- Sử dụng tính năng Function xác định cực trị của hàm số (nếu có)
Chúng ta không nên sử dụng tính năng Function, Derivative và Solver giải trực tiếp phương trình $y’=0$
Bước 3 sử dụng tính năng QR Code vẽ đồ thị hàm số
Bước 3.1 vẽ các đường tiệm cận của đồ thị (nếu có)
Bước 3.2 xác định một số điểm đặc biệt của đồ thị
- Sử dụng tính năng Function xác định giao điểm của đồ thị với trục tung
- Sử dụng tính năng Function và Equation xác định giao điểm của đồ thị với trục hoành
- Chỉ ra trục và tâm đối xứng của đồ thị (nếu có)
2 Thực hành lập bảng
Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=\frac{1}{8}x^3-\frac{3}{8}x^2-\frac{9}{8}x-\frac{5}{8}$
Bước 1 vì hàm số đã cho là hàm đa thức nên có tập xác định là R
Bước 2 xét sự biến thiên
Bước 2.1
Tìm $\lim_{x \rightarrow -\infty}y$ và $\lim_{x \rightarrow +\infty}y$
Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập $\frac{1}{8}x^3-\frac{3}{8}x^2-\frac{9}{8}x-\frac{5}{8}$ => nhấn phím EXE
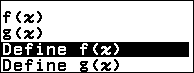
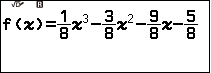
Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập $10^9$ => nhấn phím EXE
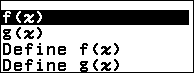
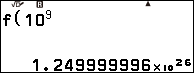
Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập $-10^9$ => nhấn phím EXE
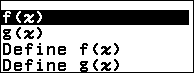
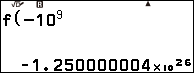
Suy ra $\lim_{x \rightarrow -\infty}y=-\infty$ và $\lim_{x \rightarrow +\infty}y=+\infty$
Vì hàm số đã cho là hàm đa thức nên đồ thị không có các đường tiệm cận
Bước 2.2 lập bảng biến thiên của hàm số
$y’=\frac{3}{8}x^2-\frac{6}{8}x-\frac{9}{8}$
Tìm nghiệm của phương trình $y’=0$
Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím EXE


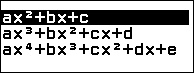
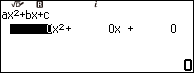
Nhập $\frac{3}{8}$ => nhấn phím EXE => nhập $-\frac{6}{8}$ => nhấn phím EXE => nhập $-\frac{9}{8}$ => nhấn phím EXE
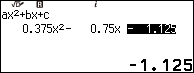
Nhấn phím EXE => nhấn phím EXE
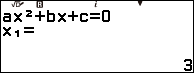
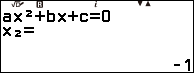
Suy ra phương trình $y’=0$ có nghiệm là $x=3$ hoặc $x=-1$
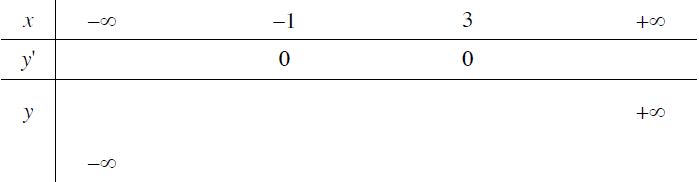
Xác định các khoảng đồng biến, nghịch biến
Nhấn phím HOME => chọn Calculate => nhấn phím OK


Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

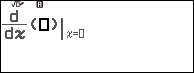
Để xác định dấu của mỗi khoảng chúng ta sẽ chọn ra một giá trị đại diện (giá trị bất kỳ thuộc khoảng), tính giá trị của $y’$ tại giá trị đại diện, nếu kết quả dương thì khoảng đang xét mang dấu cộng và ngược lại
Nhấn phím FUNCTON => chọn f(x) => nhấn phím OK => nhập x) => nhấn phím SHIFT => nhấn phím ![]() => nhập -2 => nhấn phím EXE
=> nhập -2 => nhấn phím EXE
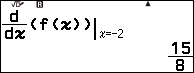
Nhấn phím FUNCTON => chọn f(x) => nhấn phím OK => nhập x) => nhấn phím SHIFT => nhấn phím ![]() => nhập 0 => nhấn phím EXE
=> nhập 0 => nhấn phím EXE
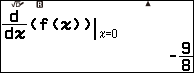
Nhấn phím FUNCTON => chọn f(x) => nhấn phím OK => nhập x) => nhấn phím SHIFT => nhấn phím ![]() => nhập 4 => nhấn phím EXE
=> nhập 4 => nhấn phím EXE
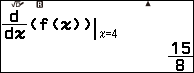
Suy ra hàm số đồng biến trên mỗi khoảng $(-\infty, -1)$ và $(3, +\infty)$, nghịch biến trên khoảng $(-1, 3)$
Xác định cực đại, cực tiểu
Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập -1 => nhấn phím EXE
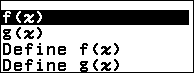

Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập 3 => nhấn phím EXE
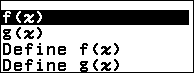

Suy ra
- Hàm số đạt cực đại tại điểm $x=-1$ và giá trị cực đại của hàm số là $y(-1)=0$
- Hàm số đạt cực tiểu tại điểm $x=3$ và giá trị cực tiểu của hàm số là $y(3)=-4$
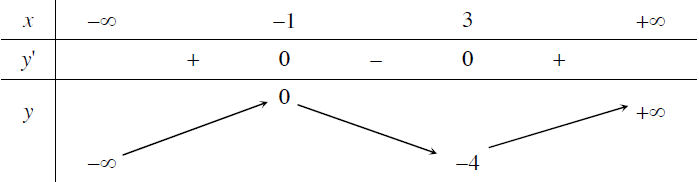
Bước 3 vẽ đồ thị hàm số
Bước 3.1 vì hàm số là hàm đa thức nên đồ thị không có các đường tiệm cận
Bước 3.2
Xác định giao điểm của đồ thị với trục tung
Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập 0 => nhấn phím EXE

Suy ra giao điểm của đồ thị với trục tung là $\left(0, -\frac{5}{8}\right)$
Xác định giao điểm của đồ thị với trục hoành
Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK


Nhập $\frac{1}{8}$ => nhấn phím EXE => nhập $-\frac{3}{8}$ => nhấn phím EXE => nhập $-\frac{9}{8}$ => nhấn phím EXE => nhập $-\frac{5}{8}$ => nhấn phím EXE
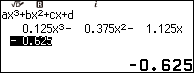
Nhấn phím EXE=> nhấn phím EXE
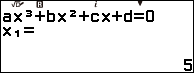
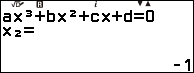
Suy ra giao điểm của đồ thị với trục hoành là $(-1, 0)$ và $(5, 0)$
Vẽ đồ thị hàm số
Ở màn hình hiển thị nghiệm của phương trình $y=0$ bạn hãy nhấn phím SHIFT => nhấn phím x => sử dụng điện thoại thông minh quét mã QR Code sẽ thu được đồ thị của hàm số đã cho
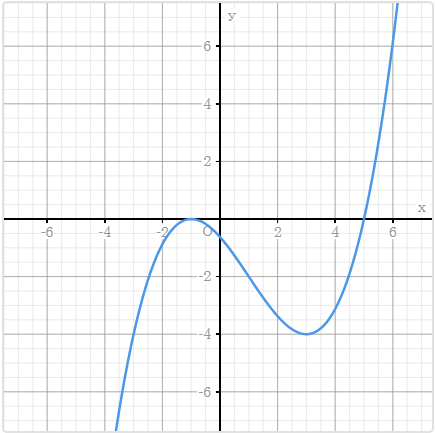
https://youtu.be/xAQXrMuzJEU
3 Lời kết
Không một tính năng nào của máy tính cầm tay CASIO fx 880 BTG cho phép chúng ta lập trực tiếp bảng biến thiên, muốn lập được chúng ta phải sử dụng kết hợp khá nhiều tính năng
Dù vậy, việc sử dụng các tính năng của máy tính cầm tay cũng giúp chúng ta lập được bảng biến thiên chính xác và khá nhanh
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp