Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn thủ thuật chuyển / biểu diễn phân số thành liên phân số hữu hạn bằng máy tính cầm tay CASIO fx 880 BTG
Thủ thuật này tuy không nhanh bằng thủ thuật ban hành giải thuật lập trình nhưng vẫn nhanh hơn nhiều so với việc chuyển bằng phương pháp Toán học thuần túy
1 Sơ lược về liên phân số hữu hạn
Cho phân số $\frac{a}{b}$ với $a, b$ là những số nguyên, $b$ lớn hơn $0$
Lúc bấy giờ áp dụng thuật toán Euclide cho hai số nguyên $a, b$ ta sẽ chuyển được phân số $\frac{a}{b}$ sang liên phân số hữu hạn $[q_0; q_1, q_2, \dots, q_n]$
$\frac{a}{b}=q_0+\frac{1}{q_1+\frac{1}{q_2+\frac{1}{\cdots+\frac{1}{q_n}}}}$
- Biểu thức $q_0+\frac{1}{q_1+\frac{1}{q_2+\frac{1}{\cdots+\frac{1}{q_n}}}}$ được gọi là liên phân số hữu hạn cấp $n$
- $q_0$ là số nguyên, $q_1, q_2, \dots, q_n$ là những số nguyên dương và $q_n > 1$
- $q_s$ được gọi là số hạn thứ $s$ của liên phân số
Mỗi liên phân số hữu hạn biểu thị cho một số hữu tỉ và mỗi số hữu tỉ đều có thể biểu diễn dưới dạng một liên phân số hữu hạn
2 Các bước chuyển / biểu diễn
Giả sử mình cần chuyển phân số $\frac{a}{b}$ thành liên phân số hữu hạn thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Bước 1 tìm $q_0$
Bước 1.1 nhập tử số a
Bước 1.2 nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Remainder => nhấn phím OK
Bước 1.3 nhập mẫu số b => nhấn phím EXE
Lúc bấy giờ chúng ta sẽ tìm được thương $q_0$ và số dư $r_0$
Bước 2 tìm $q_1$
Bước 2.1 chỉnh sửa biểu thức đang hiển thị trên màn hình máy tính cầm tay thành $A \div R F$
Bước 2.2 nhấn phím VARIABLE => nhập mẫu số b => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
Lúc bấy giờ chúng ta sẽ tìm được thương $q_1$ và số dư $r_1$
Bước 3 tìm $q_2$
Nhấn phím VARIABLE => nhập thương $r_1$=> nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
Lúc bấy giờ chúng ta sẽ tìm được thương $q_2$ và số dư $r_2$
Bước 4, Bước 5, Bước 6, …
Thực hiện tương tự Bước 3 đến khi nào số dư $r_n$ bằng $0$ thì dừng thủ thuật và kết luận liên phân số hữu hạn
3 Thực hành chuyển / biểu diễn
Chẳng hạn mình cần chuyển phân số $\frac{289}{113}$ thành liên phân số hữu hạn thì thực hiện tuần tự theo các bước bên dưới
Bước 1 tìm $q_0$
Bước 1.1 nhập 289

Bước 1.2 nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Remainder => nhấn phím OK



Bước 1.3 nhập 113 => nhấn phím EXE


Ghi nháp [2;]
Bước 2 tìm $q_1$
Bước 2.1 chỉnh sửa biểu thức đang hiển thị trên màn hình máy tính cầm tay thành $A \div R F$

Bước 2.2 nhấn phím VARIABLE => nhập 113 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
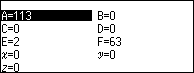
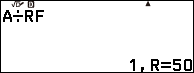
Ghi nháp [2;1]
Bước 3 tìm $q_2$
Nhấn phím VARIABLE => nhập 63 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
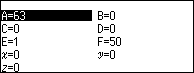
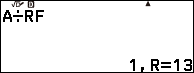
Ghi nháp [2; 1, 1]
Bước 4 tìm $q_3$
Nhấn phím VARIABLE => nhập 50 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
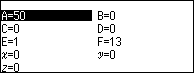
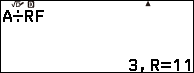
Ghi nháp [2; 1, 1, 3]
Bước 5 tìm $q_4$
Nhấn phím VARIABLE => nhập 13 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
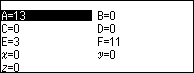

Ghi nháp [2; 1, 1, 3, 1]
Bước 6 tìm $q_5$
Nhấn phím VARIABLE => nhập 11 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
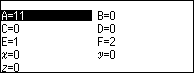

Ghi nháp [2; 1, 1, 3, 1, 5]
Bước 7 tìm $q_6$
Nhấn phím VARIABLE => nhập 2 => nhấn phím EXE => nhấn phím BACK => nhấn phím EXE
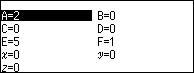

Ghi nháp [2; 1, 1, 3, 1, 5, 2]
Vì số dư $R=0$ nên chúng ta dừng thủ thuật và kết luận liên phân số hữu hạn
Vậy liên phân số hữu hạn cần tìm là [2; 1, 1, 3, 1, 5, 2]
Xem thêm Chuyển liên phân số hữu hạn thành phân số và Chuyển số vô tỉ sang liên phân số vô hạn
https://youtu.be/2RgR-nqnqOM
4 Lời kết
Đến đây mình đã hướng dẫn cho các bạn xong thủ thuật chuyển / biểu diễn phân số thành liên phân số hữu hạn bằng máy tính cầm tay CASIO fx 880 BTG
Các tính năng được sử dụng trong thủ thuật này là …
- Tính năng tìm thương và dư của phép chia Remainder
- Biến nhớ VARIABLE
- Tính năng tự động lưu thương vào biến nhớ E, số dư vào biến nhớ F
Xin chào tạm biệt và hạn gặp lại các bạn trong những bài viết tiếp theo