Chuyển nghiệm vô tỉ sang nghiệm căn thức bằng CASIO fx 880 BTG

25/10/202202/03/2023Nhut Nguyen Minh

Tính năng Solver của máy tính cầm tay CASIO fx 880 BTG cho phép chúng ta dò tìm nghiệm của một phương trình bất kì

Tuy nhiên, tính năng này cũng có một số hạn chế nhất định như …

Nếu phương trình có nhiều nghiệm thì chỉ tìm được một nghiệm
Nếu nghiệm tìm được là nghiệm hữu tỉ thì nghiệm sẽ hiển thị dưới dạng thập phân hữu hạn hoặc thập phân vô hạn tuần hoàn
Nếu nghiệm tìm được là nghiệm vô tỉ thì nghiệm sẽ hiển thị dưới dạng thập phân vô hạn không hoàn

Khi giải phương trình chúng ta luôn mong muốn tìm được tìm được tất cả các nghiệm và nghiệm sẽ được hiển thị dưới dạng phân số hoặc căn thức

Mong muốn trên sẽ thành sự thật khi chúng ta biết sử dụng thêm các thủ thuật phù hợp

Hôm nay, mình sẽ hướng dẫn các bạn cách chuyển nghiệm vô tỉ sang nghiệm căn thức bằng máy tính cầm tay CASIO fx 880 BTG

Mục lục nội dung

1 Các bước thực hiện

Bước 1 sử dụng tính năng Solver do tìm nghiệm của phương trình vô tỉ

Bước 2 gán nghiệm vô tỉ vừa tìm được vào biến nhớ A

Bước 3 mở ứng dụng tính toán thông thường Calculate

Bước 3.1 Ghi nhớ “dấu của nghiệm”

Bước 3.2 Nếu biểu thức $\sqrt{A^2}$ hiển thị được dưới dạng “căn bậc hai của một số hữu tỉ” thì nghiệm của phương trình đã cho bằng “dấu của nghiệm” “căn bậc hai của một số hữu tỉ”

Bước 3 chỉ khả dụng trong một số trường hợp, nếu không chuyển được thì thực hiện tiếp các bước bên dưới …

Bước 4 mở ứng dụng bảng giá trị Table

Bước 4.1 cài đặt chỉ sử dụng hàm f(x)

Bước 4.2 gán biểu thức $A^2+Ax$ vào hàm nhớ f(x)

Bước 4.3 khai báo Start = -22, End = 22, Step = 1

Bước 5 quan sát cột f(x) và cố gắng tìm ra một giá trị nguyên

Giả sử $f(x_0)$ là một số nguyên, lúc bấy giờ A sẽ là nghiệm của phương trình bậc hai $x^2+x_0x-f(x_0)=0$

Bước 6 sử dụng tính năng Equation giải phương trình bậc hai một ẩn $x^2+x_0x-f(x_0)=0$

2 Ví dụ minh họa

Chẳng hạn 1 mình cần giải phương trình vô tỉ $\sqrt{2x+3}-x=1$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 sử dụng tính năng Solver do tìm nghiệm của phương trình vô tỉ $\sqrt{2 x + 3}-x=1$

Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

Nhập phương trình $\sqrt{2 x + 3}-x=1$

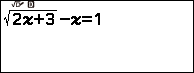
Nhấn phím OK => nhập 0 => nhấn phím OK => nhấn phím OK

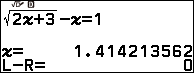
Xem thêm Cách dò tìm nghiệm Solver của phương trình

Bước 2 gán nghiệm vô tỉ vừa tìm được vào biến nhớ A

Nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK

Xem thêm Cách gán nghiệm của phương trình vào biến nhớ

Bước 3 mở ứng dụng tính toán thông thường Calculate

Nhấn phím HOME => chọn Calculate => nhấn phím OK

Bước 3.1 dễ thấy dấu của nghiệm vô tỉ vừa tìm được là “cộng”

Bước 3.2 nhập biểu thức $\sqrt{A^2}$ => nhấn phím EXE

Vậy nghiệm của phương trình đã cho là $+\sqrt{2}=\sqrt{2}$

Chẳng hạn 2 mình cần giải phương trình vô tỉ $\sqrt{2x+3}+7=x$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 sử dụng tính năng Solver do tìm nghiệm của phương trình vô tỉ $\sqrt{2x+3}+7=x$

Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

Nhập phương trình $\sqrt{2x+3}+7=x$

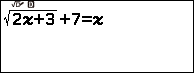
Nhấn phím OK => nhập 0 => nhấn phím OK => nhấn phím OK

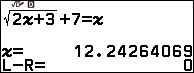
Bước 2 gán nghiệm vô tỉ vừa tìm được vào biến nhớ A

Nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK

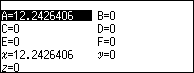
Bước 3 mở ứng dụng tính toán thông thường Calculate

Nhấn phím HOME => chọn Calculate => nhấn phím OK

Bước 3.1 dễ thấy dấu của nghiệm vô tỉ vừa tìm được là “cộng”

Bước 3.2 nhập biểu thức $\sqrt{A^2}$ => nhấn phím EXE

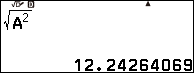
Vì biểu thức $\sqrt{A^2}$ không chuyển được nghiệm vô tỉ sang nghiệm căn thức nên chúng ta thực cần thực hiện tiếp các bước bên dưới

Bước 4 mở ứng dụng bảng giá trị Table

Nhấn phím HOME => chọn Table => nhấn phím OK

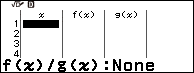
Bước 4.1 cài đặt chỉ sử dụng hàm f(x)

Nhấn phím TOOLS => chọn Table Type => nhấn phím OK => chọn f(x) => nhấn phím OK => nhấn phím AC

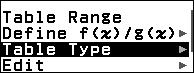
Bước 4.2 gán hàm $A^2+Ax$ vào hàm nhớ f(x)

Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK => nhập $A^2+Ax$ => nhấn phím EXE

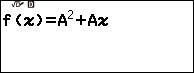
Bước 4.3 khai báo Start = -22, End = 22, Step = 1

Nhấn phím TOOLS => chọn Table Range => nhấn phím OK => nhập -22 => nhấn phím OK => nhập 22 => nhấn phím OK => nhập 1 => nhấn phím OK => nhấn phím OK

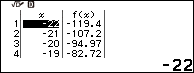
Xem thêm Cách tạo bảng giá trị Table

Bước 5 quan sát cột f(x) và cố gắng tìm một giá trị nguyên

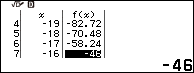
Dễ thấy $f(-16)=-46$ là một số nguyên

Lúc bấy giờ nghiệm của phương trình vô tỉ đã cho cũng là nghiệm của phương trình bậc hai một ẩn $x^2-16x+46=0$

Có vô số phương trình bậc hai một ẩn nhận nghiệm của phương trình vô tỉ làm nghiệm nhưng không phải bao giờ chúng ta cũng tìm được một cách dễ dàng

Bước 6 sử dụng tính năng Equation giải phương trình bậc hai một ẩn $x^2-16x+46=0$

Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK

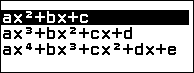
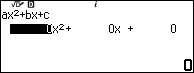
Nhập 1 => nhấn phím EXE => nhập -16 => nhấn phím EXE => nhập 46 => nhấn phím EXE

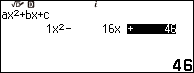
Nhấn phím EXE

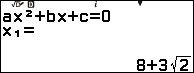
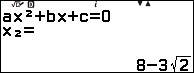
Xem thêm Cách giải phương trình bậc hai một ẩn

Tuy phương trình $x^2-16x+46=0$ có hai nghiệm nhưng chúng ta dễ dàng phân biệt được đâu là nghiệm của phương trình vô tỉ đã cho

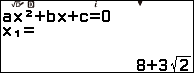
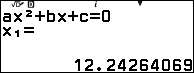
Vậy nghiệm của phương trình đã cho là $8+3\sqrt{2}$

Xem thêm Cách chuyển nghiệm thập phân sang nghiệm phân số

3 Lời kết

Bằng cách kết hợp các tính năng của máy tính cầm tay CASIO fx 880 BTG chúng ta đã chuyển được nghiệm vô tỉ sang nghiệm căn thức một cách khá dễ dàng

Trong trường hợp không may, không chuyển được (cột f(x) không có giá trị nguyên) thì bạn hãy thay đổi các giá trị Start, End, Step

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo

5 thoughts on “Chuyển nghiệm vô tỉ sang nghiệm căn thức bằng CASIO fx 880 BTG”

Nguyễn Minh Đạt
28/11/2022 at 21:00
Dạ trong khi Dễ thấy f(-16)=-46 là một số nguyên
Bước 6 sử dụng tính năng Equation giải phương trình bậc hai một ẩn x^2-16x+46=0
Sao mình lại lấy là dương 46 ạ em chưa hiểu thầy ơiii
Với lại star: -22
end: 22
Step: 1
Này thầy cho máy tính chạy max 45 giá trị nên lấy khoảng là -22 tới 22 đúng không thầy.
- Nhut Nguyen Minh
  28/11/2022 at 21:44
  Ý thứ nhất ở đây mình sử dụng hàm A^2+Ax nên khi tìm được f(-16)=-46 thì suy ra phương trình bậc hai là x^2-16x=-46 tương đương x^2-16x+46=0
  Ý thứ nhì star: -22 và end: 22 và step: 1 là những giá trị thường được sử dụng, tuy nhiên không phải bao giờ với star: -22 và end: 22 và step: 1 cũng tìm được phương trình bậc hai
  - Nguyễn Minh Đạt
    01/12/2022 at 16:26
    Dạ em cảm ơn thầy nhiều ạ
Võ Sĩ Đạt
05/03/2023 at 22:33
Tại sao lại chọn A bình + Ax để quét table vậy thầy !!!
- Nhut Nguyen Minh
  06/03/2023 at 07:41
  Dựa vào phương trình bậc hai một ẩn ax^2+bx+c=0 đó bạn, giải thích khá dài dòng, nếu bạn muốn biết chi tiết vui lòng Inbox cho mình thông qua địa chỉ https://www.facebook.com/nnmnhut

1 Các bước thực hiện

2 Ví dụ minh họa

3 Lời kết

5 thoughts on “Chuyển nghiệm vô tỉ sang nghiệm căn thức bằng CASIO fx 880 BTG”

Trả lời Hủy