Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn cho các bạn chi tiết các bước sử dụng chức năng tạo bảng giá trị Table và chức năng tính đạo hàm tại một điểm Derivative của máy tính cầm tay CASIO fx 880 BTG xác định số điểm cực trị của hàm số
Trong phạm vi ngắn gọn của bài viết này chúng ta chỉ xác định số điểm cực trị của hàm số trong khoảng hoặc nữa khoảng hoặc đoạn
Xem thêm Xác định số nghiệm của phương trình bằng máy tính cầm tay
1 Các bước xác định
Giả sử mình cần xác định số điểm cực trị của hàm số h(x) trong khoảng (a, b) thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Bước 1 mở ứng dụng bảng giá trị Table
Bước 2 cài đặt chỉ sử dụng hàm f(x)
Bước 3 khai báo f(x) là $\frac{d}{dx}(h(x))|_{x=x}$
Bước 4 khai báo Start=a, End=b và $Step=(b-a) \div 44$
Bước 5 xác định số lần đổi dấu của f(x), có bao nhiêu lần đổi dấu thì có bấy nhiêu điểm cực trị
- Nếu dấu của đạo hàm thay đổi n lần từ dương sang âm thì hàm số có n điểm cực đại
- Nếu dấu của đạo hàm thay đổi n lần từ âm sang dương thì hàm số có n điểm cực tiểu

2 Thực hành xác định
Chẳng hạn mình cần xác định số điểm cực trị của hàm số $y=x-\sin 2x+3$ trong khoảng $(-\frac{\pi}{3}, 4 \pi)$ thì thực hiện tuần tự theo các bước bên dưới
Vì hàm số đã cho có chứa các hàm số lượng giác (sin) nên cần cài đặt đơn vị góc là rađian trước khi thực hiện
Xem thêm Cài đặt đơn vị góc (Độ, Rađian, Građian)
Bước 1 mở ứng dụng bảng giá trị Table
Nhấn phím HOME => chọn Table => nhấn phím OK


Bước 2 cài đặt chỉ sử dụng hàm f(x)
Nhấn phím TOOLS => chọn Table Type => nhấn phím OK => chọn f(x) => nhấn phím OK => nhấn phím AC



Bước 3 khai báo f(x) là $\frac{d}{dx}(x-\sin 2x+3)|_{x=x}$
Bước 3.1 nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK



Bước 3.2 nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative (d / dx) => nhấn phím OK => nhập $\frac{d}{dx}(x-\sin 2x+3)|_{x=x}$



Bước 3.3 nhấn phím OK

Bước 4 khai báo $Start=-\frac{\pi}{3}, End=4\pi$ và $Step=(4\pi–\frac{\pi}{3}) \div 44$
Nhấn phím TOOLS => chọn Table Range => nhấn phím OK => nhập $-\frac{\pi}{3}$ => nhấn phím EXE => nhập $4\pi$ => nhấn phím EXE => nhập $(4\pi–\frac{\pi}{3}) \div 44$ => nhấn phím EXE => nhấn phím EXE
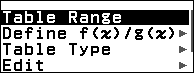
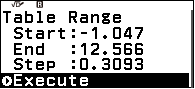

Bước 5 xác định số lần đổi dấu của f(x), có bao nhiêu lần đổi dấu thì có bấy nhiêu điểm cực trị

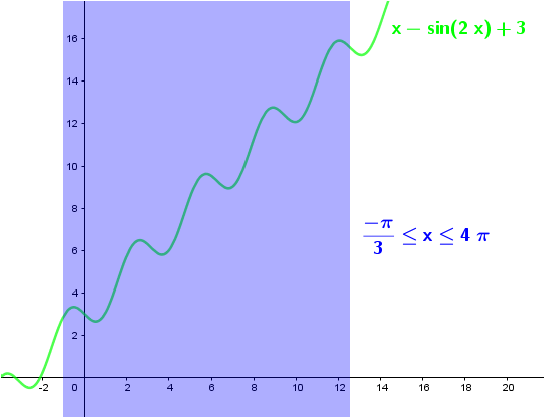
Dựa vào bảng giá trị vừa tìm được chúng ta dễ dàng nhận thấy dấu của đạo hàm thay đổi 5 từ dương sang âm nên hàm số có 5 điểm cực đại
Vậy số điểm cực trị (cực đại) của hàm số $x-\sin 2 x+3$ trong khoảng $(-\frac{\pi}{3}, 4 \pi)$ là 5
https://youtu.be/TX46rPwa81A
3 Lời kết
Việc sử dụng khéo léo chức năng tạo bảng giá trị Table và chức năng tính đạo hàm tại một điểm Derivative của máy tính cầm tay CASIO fx 880 BTG cho phép chúng ta xác định chính xác và nhanh chóng số điểm cực trị của hàm số trong một khoảng nào đó
Việc xác định số điểm cực trị của hàm số trên tập xác định hoặc xác định chính xác tọa độ của điểm cực trị của hàm số cần thực hiện thêm một số thao tác phù hợp
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
Tài liệu tham khảo
Nguyễn Thành Nhân, Nghiên cứu ứng dụng chức năng Table của máy tính CASIO fx-580VN X vào hỗ trợ giải một số dạng toán phổ thông, Tạp chí Khoa học Đại học Đồng Tháp, Tập 9, Số 3, 2020, 3-12