Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn cách tính khoảng cách giữa hai điểm cực trị của hàm số bằng máy tính cầm tay CASIO fx 880 BTG

1 Khoảng cách giữa hai điểm cực trị của hàm số bậc ba
Chẳng hạn mình cần tính khoảng cách giữa hai điểm cực trị của hàm số bậc ba $y=x^3-3x^2+2x$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 giải phương trình bậc ba tương ứng
Bước 1.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK



Bước 1.2 nhập các hệ số của phương trình
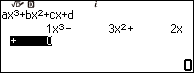
Bước 1.3 nhấn phím EXE để tìm nghiệm
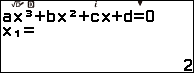
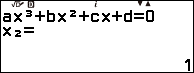

Bước 1.4 nhấn phím EXE để tìm hai điểm cực trị
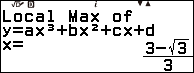
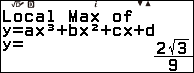
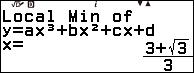
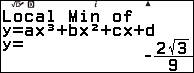
Xem thêm Cách tìm cực trị của hàm số bậc ba
Bước 2 gán hoành độ, trung độ của hai điểm cực trị vào các biến nhớ
Bước 2.1 nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK
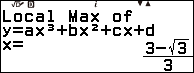
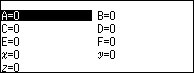

Bước 2.2 nhấn phím VARIABLE => chọn biến nhớ B => nhấn phím OK => chọn Store => nhấn phím OK
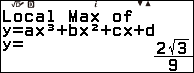
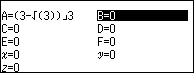

Bước 2.3 nhấn phím VARIABLE => chọn biến nhớ C => nhấn phím OK => chọn Store => nhấn phím OK
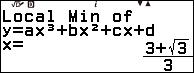


Bước 2.4 nhấn phím VARIABLE => chọn biến nhớ D => nhấn phím OK => chọn Store => nhấn phím OK
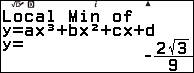
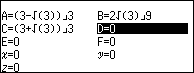

Tóm lại chúng ta đã gán được …
- Hoành độ, trung độ của điểm cực đại vào biến nhớ A, B
- Hoành độ, trung độ của điểm cực tiểu vào biến nhớ C, D

Xem thêm Cách gán nghiệm của phương trình vào biến nhớ
Bước 3 tính khoảng cách giữa hai điểm cực trị
Nhập biểu thức $\sqrt{\left({C-A}\right)^2+\left({D-B}\right)^2}$ => nhấn phím EXE

Vậy khoảng cách giữa hai điểm cực trị của hàm số đã cho là $\frac{2\sqrt{39}}{9}$
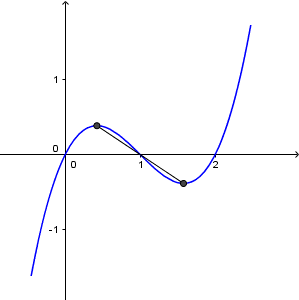
2 Khoảng cách giữa hai điểm cực trị của hàm số bất kì
Muốn tính được khoảng cách giữa hai điểm cực trị của hàm số bất kì bạn cần tìm chính xác hoành độ và trung độ của hai điểm cực trị trước
Bạn có thể sử dụng kiến thức Toán học hoặc thủ thuật máy tính cầm tay
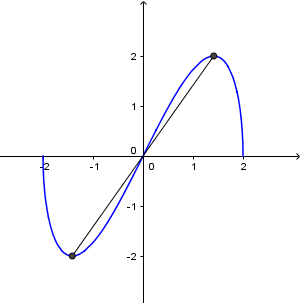
Chẳng hạn mình cần tính khoảng cách giữa hai điểm cực trị của hàm số $y=x\sqrt{-x^2+4}$ thì thực hiện tuần tự theo các bước bên dưới
Bước i thực hiện theo các chỉ dẫn trong bài viết cách tìm cực trị của một hàm số bất kì chúng ta sẽ tìm được hoành độ và trung độ của hai điểm cực trị
Bước ii gán hoành độ và trung độ của hai điểm cực trị vào các biến nhớ
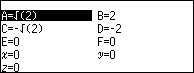
Bước iii tính giá trị biểu thức $\sqrt{\left({C-A}\right)^2+\left({D-B}\right)^2}$
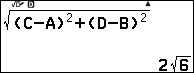
Vậy khoảng cách giữa hai điểm cực trị của hàm số đã cho là $2\sqrt{6}$
https://youtu.be/HehukinbzGc
3 Lời kết
Ngoài thủ thuật tính khoảng cách giữa hai điểm cực trị của hàm số, máy tính cầm tay CASIO fx 880 BTG còn hỗ trợ chúng ta các thủ thuật khác có liên quan đến hai điểm cực trị như …
- Viết phương trình đường thẳng đi qua hai điểm cực trị
- Trung điểm của đoạn thẳng cực trị
- Viết phương trình đường trung trực của đường thẳng đi qua hai điểm cực trị
- …
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo