Tính năng Solver trên máy tính cầm tay CASIO fx 880 BTG chính là tính năng SOLVE trên các dòng máy tính cầm tay tiền nhiệm
Tính năng Solver cho phép chúng ta dò tìm nghiệm của một phương trình bất kì (đa thức, phân thức, vô tỉ, …)
Tuy nhiên, tính năng này vẫn có một số hạn chế nhất định, dễ thấy nhất là nếu phương trình có nhiều nghiệm thì chỉ tìm ra một nghiệm
Hôm nay, mình sẽ hướng dẫn các bạn cách tìm tất cả các nghiệm của phương trình bằng tính năng Solver của máy tính cầm tay CASIO fx 880 BTG
1 Các bước thực hiện
Giả sử chúng ta cần dò tìm tất cả các nghiệm của phương trình $f(x)=0$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 sử dụng tính năng Solver dò tìm nghiệm của phương trình $f(x)=0$
Bước 2
- Giả sử tìm được nghiệm $x_1$
- Gán $x_1$ vào biến nhớ A
Bước 3 sử dụng tính năng Solver dò tìm nghiệm của phương trình $f(x) \div (x-A)$
Bước 4
- Giả sử tìm được nghiệm $x_2$
- Gán $x_2$ vào biến nhớ $B$
Bước 5 sử dụng tính năng Solver dò tìm nghiệm của phương trình $f(x) \div (x-A) \div (x-B)$
Bước 6
- Nếu tìm được nghiệm $x_3$ thì gán $x_3$ vào biến nhớ $C$ và tiếp tục sử dụng tính năng Solver dò tìm nghiệm của phương trình $f(x) \div (x-A) \div (x-B) \div (x-C)$
- Nếu thông báo Cannot Solve xuất hiện thì dừng quá trình dò tìm nghiệm và kết luận tập nghiệm của phương trình
2 Một số thông báo
Trong quá trình dò tìm nghiệm của phương trình chắc chắn bạn sẽ gặp thông báo Cannot Solve hoặc Continue
2.1 Cannot Solve
Thông báo Cannot Solve có nghĩa là không tìm được nghiệm, không tìm được nghiệm không có nghĩa là phương trình vô nghiệm
Khi gặp thông báo này mà chúng ta kết luận phương trình vô nghiệm thì cũng có rủi ro nhất định
Tuy nhiên, với hầu hết các phương trình đại số (đa thức, phân thức, vô tỉ) thì thông báo Cannot Solve gần như đồng nhất với phương trình vô nghiệm
2.2 Continue
Khi gặp thông báo Continue bạn hãy nhấn phím EXE để tiếp tục quá trình dò tìm nghiệm
3 Ví dụ minh họa
Chẳng hạn mình cần dò tìm tất cả các nghiệm của phương trình $x(29+10x)=-21$ thì thực hiện tuần tự theo các bước bên dưới
Dễ thấy phương trình đã cho tương đương với $x(29+10x)+21=0$
Bước 1 sử dụng tính năng Solver dò tìm nghiệm của phương trình $x(29+10x)+21=0$
Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK



Nhập $x(29+10x)+21$
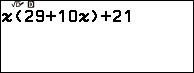
Nhấn phím OK => nhập 0 => nhấn phím OK => nhấn phím OK


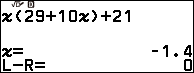
Xem thêm Cách dò tìm nghiệm Solver của phương trình
Bước 2 gán nghiệm $x=-1.4$ vừa tìm được vào biến nhớ A
Nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK
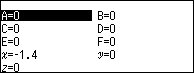

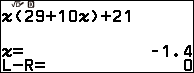
Xem thêm Cách gán nghiệm của phương trình vào biến nhớ
Bước 3
Nhấn phím EXE => chỉnh sửa phương trình hiện tại thành phương trình $\left({x\left({29+10x}\right)+21}\right) \div \left({x-A}\right)$
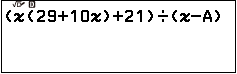
Nhấn phím OK => chọn x => nhập 0 => nhấn phím OK => nhấn phím OK


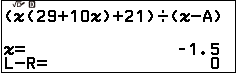
Bước 4 gán nghiệm $x=-1.5$ vừa tìm được vào biến nhớ B
Nhấn phím VARIABLE => chọn biến nhớ B => nhấn phím OK => chọn Store => nhấn phím OK
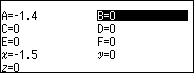

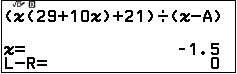
Bước 5
Nhấn phím EXE => chỉnh sửa phương trình hiện tại thành phương trình $\left({x\left({29+10x}\right)+21}\right) \div \left({x-A}\right) \div \left({x-B}\right)$
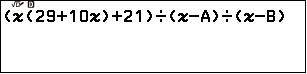
Nhấn phím OK => chọn x => nhập 0 => nhấn phím OK => nhấn phím OK




Vậy tập nghiệm của phương trình đã cho là $\{-\frac{7}{5}, -\frac{3}{2}\}$
Khi dò tìm được các nghiệm là số tự nhiên, số nguyên, số thập phân hữu hạn thì có thể nhập trực tiếp không cần gán vào các biến nhớ
Xem thêm Cách chuyển nghiệm thập phân sang nghiệm phân số
4 Bài tập thực hành
Dò tìm tất cả các nghiệm của phương trình $\frac{x^2(x^2-1)–2}{x^2+1}=0$ bằng máy tính cầm tay CASIO fx 880 BTG
Gợi ý
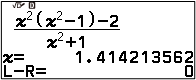
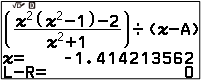
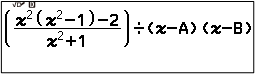

Vậy tập nghiệm của phương trình đã cho là $\{\sqrt{2}, \sqrt{2}\}$
Xem thêm Cách chuyển nghiệm vô tỉ sang nghiệm căn thức
https://youtu.be/rqJkLx5f9S0
5 Lời kết
Thủ thuật dò tìm tất cả các nghiệm của phương trình bằng tính năng Solver của máy tính cầm tay CASIO fx 880 BTG là một trong những thủ thuật kinh điển, có nhiều ứng dụng trong học tập, kiểm tra và thi cử
Thủ thuật này vẫn có thể thực hiện được trên các dòng máy tính cầm tay tiền nhiệm, tuy nhiên trên CASIO fx 880 BTG sẽ cho ra kết quả nhanh nhất
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo