Xin chào tất cả các bạn
Hôm nay mình sẽ hướng dẫn các bạn cách tìm đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số bằng máy tính cầm tay CASIO fx 880 BTG

1 Kiến thức Toán học
Đường thẳng $y=y_0$ được gọi là đường tiệm cận ngang của đồ thị hàm số $y=f(x)$ nếu $\lim_{x \rightarrow +\infty} f(x)=y_0$ hoặc $\lim_{x \rightarrow -\infty} f(x)=y_0$
Đường thẳng $x=x_0$ được gọi là đường tiệm cận đứng của đồ thị hàm số $y=f(x)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn
- $\lim_{x \rightarrow x_0^-} f(x)=+\infty$
- $\lim_{x \rightarrow x_0^-} f(x)=-\infty$
- $\lim_{x \rightarrow x_0^+} f(x)=+\infty$
- $\lim_{x \rightarrow x_0^+} f(x)=-\infty$
Bạn chỉ cần nhớ được hai mảng kiến thức này và biết cách tính giới hạn của hàm số là sẽ tìm được đường tiệm cận một cách chính xác và nhanh chóng
Xem thêm Cách tính giới hạn của hàm số
2 Các bước tìm đường tiệm cận ngang
Chẳng hạn mình cần tìm đường tiệm cận ngang của đồ thị hàm số $f(x)=\frac{1}{\sqrt{x}}+1$ xác định trên khoảng $(0; +\infty)$ thì thực hiện tuần tự theo các bước bên dưới
Gợi ý
- Nếu chúng ta tìm được $\lim_{x \rightarrow +\infty} \left(\frac{1}{\sqrt{x}}+1\right)$ bằng một số thực nào đó thì đường tiệm cận ngang của đồ thị hàm số đã cho chính là y = “số thực vừa tìm được”
- Nếu không tìm được số thực nào hết thì hàm số đã cho không có đường tiệm cận ngang
Bước 1 nhập hàm số vào máy tính

Bước 2 nhấn phím TOOLS => chọn CALC => nhấn phím OK


Bước 3 nhập $10^9$ => nhấn phím EXE => nhấn phím EXE


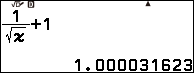
Suy ra $\lim_{x \rightarrow +\infty} f(x)=\lim_{x \rightarrow +\infty} \left(\frac{1}{\sqrt{x}}+1\right)=1$
Vậy đường tiệm cần ngang của hàm số đã cho là $y=1$
Một hàm số có thể có một hoặc hai hoặc … hoặc không có đường tiệm cận ngang
3 Các bước tìm đường tiệm cận đứng
Chẳng hạn mình cần tìm đường tiệm cận đứng của đồ thị hàm số $y=\frac{2x^2+x+1}{2x-3}$ tuần tự theo các bước bên dưới
Gợi ý
- Dễ thấy $\frac{3}{2}$ là giá trị làm cho hàm số không xác định
- Nếu chúng ta tìm được $\lim_{x \rightarrow \left(\frac{3}{2}\right)^+} \frac{2x^2+x+1}{2x-3}$ hoặc $\lim_{x \rightarrow \left(\frac{3}{2}\right)^-} \frac{2x^2+x+1}{2x-3}$ bằng vô cùng thì đường tiệm cận đứng của đồ thị hàm số đã cho chính là $x=\frac{3}{2}$
- Nếu không có giới hạn nào có kết quả là vô cùng thì hàm số đã cho không có đường tiệm cận đứng
Bước 1 nhập hàm số vào máy tính
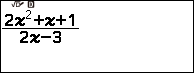
Bước 2 nhấn phím TOOLS => chọn CALC => nhấn phím OK

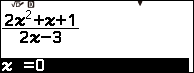
Bước 3 nhập $\frac{3}{2}+10^{-9}$ => nhấn phím EXE => nhấn phím EXE
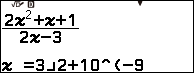
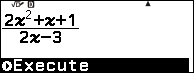
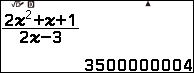
Suy ra $\lim_{x \rightarrow \left(\frac{3}{2}\right)^+} \frac{2x^2+x+1}{2x-3}=+\infty$
Vậy đường tiệm cận đứng của đồ thị hàm số đã cho là $x=\frac{3}{2}$
Một hàm số có thể có hoặc không có đường tiệm cận đứng
https://youtu.be/-CCJYMo0E5Q
4 Lời kết
Việc tìm ra các đường tiệm cận của đồ thị hàm số bằng máy tính cầm tay CASIO fx 880 BTG không có gì khó khăn, bạn chỉ cần …
- Nhớ được hai mảng kiến thức Toán học được trình bày ở đầu bài viết
- Thực hiện được thủ thuật tính giới hạn của hàm số
… là có thể tìm được một cách chính xác và nhanh chóng
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo