Tìm cực trị của một hàm số bất kì bằng CASIO fx 880 BTG

07/10/202229/08/2023Nhut Nguyen Minh

Xin chào tất cả các bạn

Hôm này mình sẽ hướng dẫn các bạn tìm chính xác và nhanh chóng cực trị của một hàm số bất kì bằng bảng tính Spreadsheet của máy tính cầm tay CASIO fx 880 BTG

Mục lục nội dung

1 Nhắc lại kiến thức Toán học

Thủ thuật máy tính cầm tay nào cũng được sáng tạo ra từ việc kết hợp kiến thức Toán học và kiến thức máy tính cầm tay

Dưới đây là hai mảng kiến thức Toán học có liên quan trực tiếp đến thủ thuật này

1.1 Các bước tìm cực trị của một hàm số

Để tìm cực trị của một hàm số f(x) chúng ta sẽ thực hiện tuần tự theo các bước bên dưới

Bước 1 tìm đạo hàm cấp một $f'(x)$

Bước 2 giải phương trình $f'(x)=0$

Giả sử chúng ta tìm được các nghiệm là $x_i$ $(i=1, 2, 3, …)$

Bước 3 tìm đạo hàm cấp hai $f''(x)$

Bước 4 tính $f''(x_i)$

Nếu $f''(x_i) < 0$ thì hàm số đạt cực đại tại $x_i$
Nếu $f''(x_i) > 0$ thì hàm số đạt cực tiểu tại $x_i$

Qua các bước giải trên chúng ta thấy quá trình tìm cực trị của một hàm số nhanh hay chậm chủ yếu phụ thuộc vào hàm f(x)

Nếu f(x) là một hàm phức tạp thì khi tính đạo hàm cấp một sẽ tốn nhiều thời gian, giải phương trình $f'(x)=0$ và tính đạo hàm cấp hai cũng vậy

1.2 Công thức tính đạo hàm cấp hai tại những điểm là nghiệm của phương trình f’(x) = 0

Nếu $x_0$ là nghiệm của phương trình $f'(x)=0$ thì $f''(x_0)$ sẽ được tính theo công thức $f''(x_0)=\lim_{h \rightarrow 0} \frac{f'(x_0+h)}{h}$

2 Các bước thực hiện

Bước 1 sử dụng tính năng FUNCTION gán hàm số f(x) vào hàm nhớ f(x)

Bước 2 sử dụng tính năng dò tìm nghiệm Solver, tính năng tính đạo hàm Derivative (d/dx) và tính năng VARIABLE để tìm nghiệm của phương trình $f'(x)=0$ và lưu các nghiệm tìm được vào các biến nhớ

Bước 3 sử dụng bảng tính Spreadsheet để tính gần đúng đạo hàm cấp hai tại những điểm là nghiệm của phương trình $f'(x)=0$

Bước 4 quan sát bảng tính rồi suy ra các điểm cực trị của hàm số đã cho

3 Ví dụ minh họa

Chẳng hạn chúng ta cần tìm cực trị của hàm số $y=x\sqrt{-x^2+4}$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1 gán hàm số $x\sqrt{-x^2+4}$ vào hàm nhớ f(x)

Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập hàm số $x\sqrt{-x^2+4}$ => nhấn phím EXE

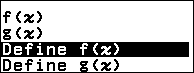
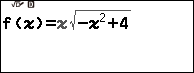
Bước 2 giải phương trình $(x\sqrt{-x^2+4})'=0$ và các lưu nghiệm tìm được vào các biến nhớ

Bước 2.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK

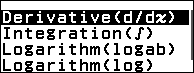
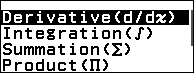
Bước 2.2 nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative (d/dx) => nhấn phím OK

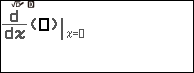
Bước 2.3 nhấn phím FUNCTION => chọn f(x) => nhấn phím OK

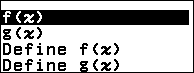
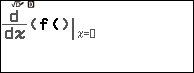
Bước 2.4 nhấn phím x => nhấn phím ) => nhấn phím x

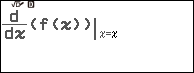
Bước 2.5 nhấn phím EXE => chọn Execute => nhấn phím EXE

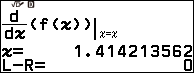
Bước 2.6 nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím OK => chọn Store => nhấn phím OK

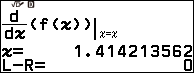
Bước 2.7 nhấn phím EXE => nhập $\div(x-A)$ => nhấn phím EXE => chọn x => nhấn phím EXE => chọn Execute => nhấn phím EXE

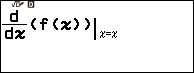
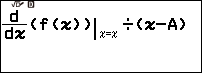
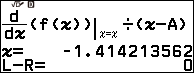
Bước 2.8 nhấn phím VARIABLE => chọn biến nhớ B => nhấn phím OK => chọn Store => nhấn phím OK

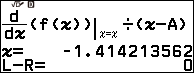
Bước 2.9 nhấn phím EXE => nhập $\div(x-B)$ => nhấn phím EXE => chọn x => nhấn phím EXE => chọn Execute => nhấn phím EXE

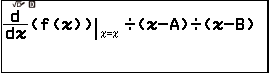
Suy ra phương trình $(x\sqrt{-x^2+4})'=0$ chỉ có hai nghiệm là hai giá trị trong biến nhớ A và biến nhớ B

Giả sử phương trình $f'(x)=0$ còn nghiệm thì tiếp tục lưu vào biến nhớ C, tiếp tục tìm các nghiệm còn lại và lưu vào các biến nhớ còn lại
Tìm thiếu nghiệm sẽ kết luận thiếu điểm cực trị

Bước 3 mở ứng dụng bảng tính Spreadsheet

Nhấn phím HOME => chọn Spreadsheet => nhấn phím OK

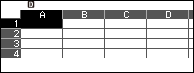
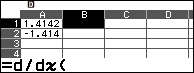
Bước 4 nhập biến nhớ A vào ô A1 => nhấn phím EXE => nhập biến nhớ B vào ô A2 => nhấn phím EXE

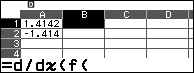
Bước 5 nhập công thức =d/x(f(x),10^(-9)+A1) vào ô B1

Bước 5.1 chọn ô B1 => nhập kí tự đặc biệt =

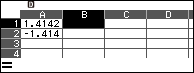
Bước 5.2

Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative (d/dx) => nhấn phím OK
Nhấn phím FUNCTION => chọn f(x) => nhấn phím OK
Nhấn phím x => nhấn phím ) => nhập , => nhập 10^(-9)+A1 => nhấn phím ) => nhấn phím EXE

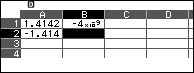
Bước 6 sao chép công thức từ ô B1 đến ô B2

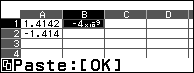
Chọn ô B1 => nhấn phím TOOLS => chọn Copy & Paste => nhấn phím OK
Chọn ô B2 => nhấn phím OK => nhấn phím AC

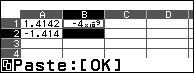
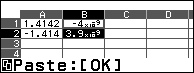
Bước 7 chọn ô C1 => nhập công thức =B1 $\div$ 10^(-9 => nhấn phím EXE

Bước 8 sao chép công thức từ ô C1 đến ô C2

Chọn ô C1 => nhấn phím TOOLS => chọn Copy & Paste => nhấn phím OK
Chọn ô C2 => nhấn phím OK => nhấn phím AC

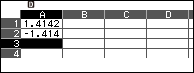
Giá trị trong ô C1 chính là giá trị gần bằng của $f''(A)$ và C2 chính là giá trị gần bằng của $f''(B)$

Biết được giá trị của đạo hàm cấp hai tại những điểm là nghiệm của phương trình $f'(x)=0$ sẽ biết được điểm cực trị của hàm số

Vậy hàm số đã cho đạt cực đại tại $x \approx1.4142$ và cực tiểu tại $x \approx-1.414$

Bước 5 và Bước 7 là thao tác tính gần đúng đạo hàm cấp hai của hàm số tại những điểm là nghiệm của phương trình $f'(x)=0$

4 Lời kết

Nhờ vào bảng tính Spreadsheet của máy tính cầm tay CASIO fx 880 BTG mà chúng ta có thể tìm chính xác và nhanh chóng các điểm cực trị của một hàm số bất kì

Ngoài tính năng tìm cực trị bảng tính Spreadsheet còn hỗ trợ chúng ta tìm giá trị lớn nhất và giá trị nhỏ nhất

Mới các bạn đoán xem thủ thuật trên trong những bài viết tiếp theo, còn bây giờ xin chào tạm biệt và hẹn gặp lại