Kế thừa những tính năng ưu việt từ máy tính cầm tay CASIO fx 580 VN X, CASIO fx 880 BTG cũng cho phép chúng ta tìm nhanh cực trị của hàm số bậc ba
Tương tự việc tìm cực trị của hàm số bậc hai, để tìm cực trị của hàm số bậc ba chúng ta cũng đi giải phương trình bậc ba tương ứng
Chẳng hạn để tìm cực trị của hàm số $f(x)=2x^3-9x^2+12x-4$ chúng ta sẽ đi giải phương trình $2x^3-9x^2+12x-4=0$
1 Các bước tìm cực trị
Bước 1 nhấn phím HOME => sử dụng các phím điều hướng 
chọn Equation => nhấn phím OK
Bước 2 chọn Polynomial => nhấn phím OK
Bước 3 chọn $ax^3+bx^2+cx+d$ => nhấn phím OK
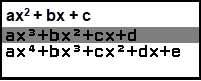
Bước 4 màn hình soạn thảo các hệ số xuất hiện, lúc bấy giờ bạn hãy nhập các hệ số của phương trình bậc ba tương ứng
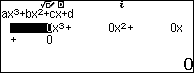
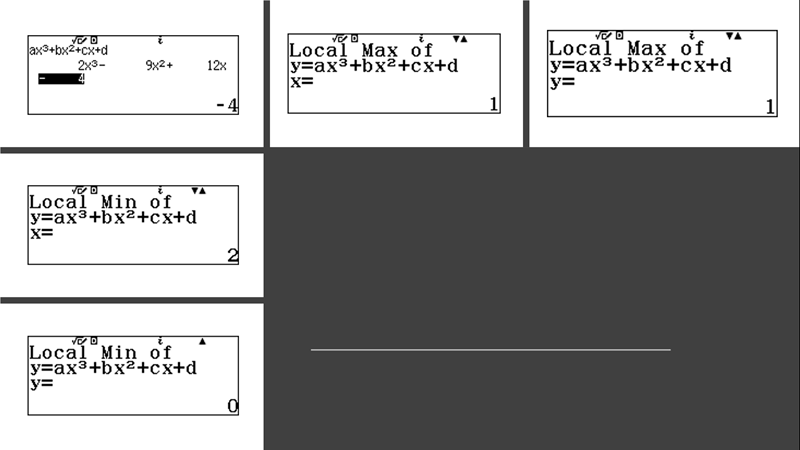
Giải sử mình cần tìm cực trị của hàm số $f(x)=2x^3-9x^2+12x-4$
Lần lượt nhấn các phím 
để nhập các hệ số $2, -9, 12, -4$ của phương trình bậc ba tương ứng
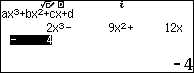
Bước 5 nhấn phím EXE để giải phương trình và hiển thị nghiệm
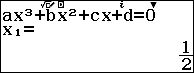
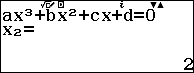
Bước 6 nhấn phím EXE để hiển thị hoành độ và trung độ của điểm cực trị (nếu có)
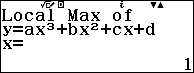
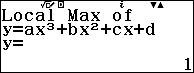
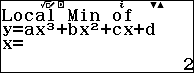
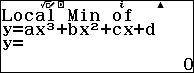
Vậy đồ thị hàm số $f(x)=2x^3-9x^2+12x-4$ có hai điểm cực trị là $(1, 1)$ và $(2, 0)$
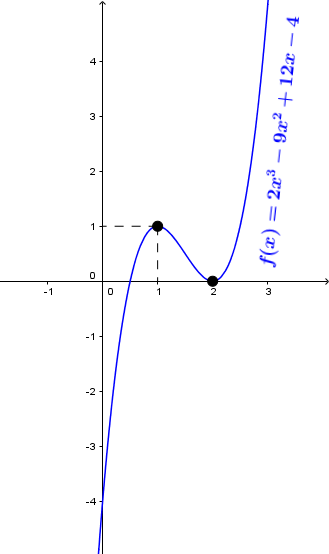
Một hàm bậc ba bất kỳ có thể có hai điểm cực trị hoặc một điểm cực trị hoặc không có điểm cực trị nào
2 Cách xác định cực trị vừa tìm được là cực đại hay cực tiểu
- Nếu màn hình xuất hiện thông báo $Local~Min~of~y=ax^3+bx^2+cx+d$ thì điểm cực trị vừa tìm được là cực tiểu
- Nếu màn hình xuất hiện thông báo $Local~Max~of~y=ax^3+bx^2+cx+d$ thì điểm cực trị vừa tìm được là cực đại
- Nếu màn hình xuất hiện thông báo No Local Max / Min thì hàm số đã cho không có cực trị
https://youtube.com/shorts/TmBd-seaGH4
3 Lời kết
Hàm số bậc ba là hàm số đa thức có bậc cao nhất mà máy tính cầm tay CASIO fx 880 BTG có thể tìm được cực trị
Hy vọng trong những phiên bản tiếp theo hãng CASIO sẽ cải tiến tính năng này, nếu có thể tìm được cực trị của hàm số bậc bốn thì sẽ là một điều rất tuyệt vời
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
