Xin chào tất cả các bạn
Hôm nay mình sẽ hướng dẫn các bạn ứng dụng phương thức tính toán Matrix của máy tính CASIO fx-580VN X vào việc chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng, bốn điểm đồng phẳng
Trường hợp muốn rèn luyện kĩ năng tính toán thì bạn có thể sử dụng các phương pháp Toán học như quy tắc Sarrus, công thức Leibniz, công thức Laplace, phép khử Gauss
Sau khi tính được định thức của ma trận vuông cấp $3 \times 3$ bạn hãy dựa vào các kết quả (đã được chứng minh) bên dưới để kết luận
1 Ba đường thẳng đồng quy trên mặt phẳng
Trên mặt phẳng $Oxy$ cho ba đường thẳng $(\Delta_1), (\Delta_2), (\Delta_3)$ cắt nhau từng đôi một và lần lượt có phương trình tổng quát
$a_1x+b_1y+c_1=0$, $a_2x+b_2y+c_2=0$, $a_3x+b_3y+c_3=0$
$(\Delta_1), (\Delta_2), (\Delta_3)$ đồng quy khi và chỉ khi $\left|\begin{array}{lll}a_1&b_1&c_1\\ a_2&b_2&c_2\\ a_3&b_3&c_3\end{array}\right|=0$
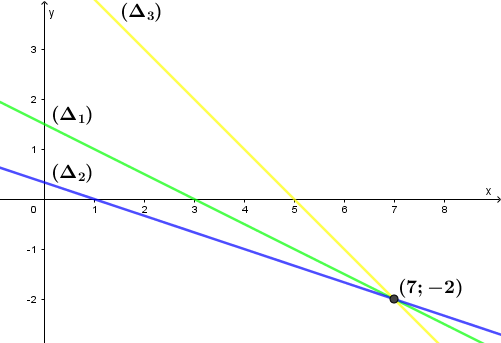
Trên mặt phẳng $Oxy$ cho ba đường thẳng $(\Delta_1):x+2y-3=0$, $(\Delta_2):x+3y-1=0$, $(\Delta_3):x+y-5=0$
Chứng minh $(\Delta_1), (\Delta_2), (\Delta_3)$ đồng quy và tìm tọa độ giao điểm
Bước 1 Định nghĩa ma trận $MatA$
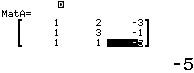
Bước 2 Tính định thức của ma trận $MatA$

Suy ra $(\Delta_1), (\Delta_2), (\Delta_3)$ đồng quy
Tọa độ giao điểm là nghiệm của hệ phương trình $\left\{\begin{array}{ll}x+2y&=3\\ x+3y&=1\end{arrow}\right.$
Vậy ba đường thẳng đã cho đồng quy và tọa độ giao điểm là $(7; -2)$
2 Ba điểm thẳng hàng
2.1 Ba điểm thẳng hàng trên mặt phẳng
Trên mặt phẳng $Oxy$ cho ba điểm $A=(x_a; y_a)$, $B=(x_b; y_b)$, $C=(x_c; y_c)$
$A, B, C$ thẳng hàng khi và chỉ khi $\left|\begin{array}{lll}x_a&y_a&1\\x_b&y_b&1\\x_c&y_c&1\end{array}\right|=0$
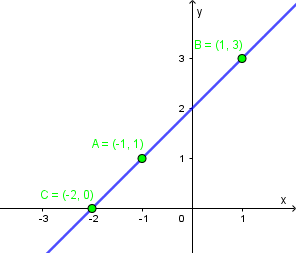
Trên mặt phẳng $Oxy$ cho ba điểm $A=(-1; 1), B=(1; 3), C=(-2; 0)$
Chứng minh $A, B, C$ thẳng hàng
Bước 1 Định nghĩa ma trận $MatA$
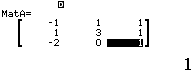
Bước 2 Tính định thức của ma trận $MatA$

Vậy ba điểm đã cho thẳng hàng
2.2 Ba điểm thẳng hàng trong không gian
Trong không gian $Oxyz$ cho ba điểm $A=(x_a; y_a; z_a)$, $B=(x_b; y_b; z_b)$, $C=(x_c; y_c; z_c)$
$A, B, C$ thẳng hàng khi và chỉ khi $\left\{\begin{array}{l}\left|\begin{array}{lll}x_a&y_a&1\\x_b&y_b&1\\x_c&y_c&1\end{array}\right|=0\\\left|\begin{array}{lll}y_a&z_a&1\\y_b&z_b&1\\y_c&z_c&1\end{array}\right|=0\end{array}\right.$
Trong không gian $Oxyz$ cho ba điểm $A=(1; -2; -1)$, $B=(4; 0; 1)$, $C=(-2; -4; -3)$
Chứng minh $A, B, C$ thẳng hàng
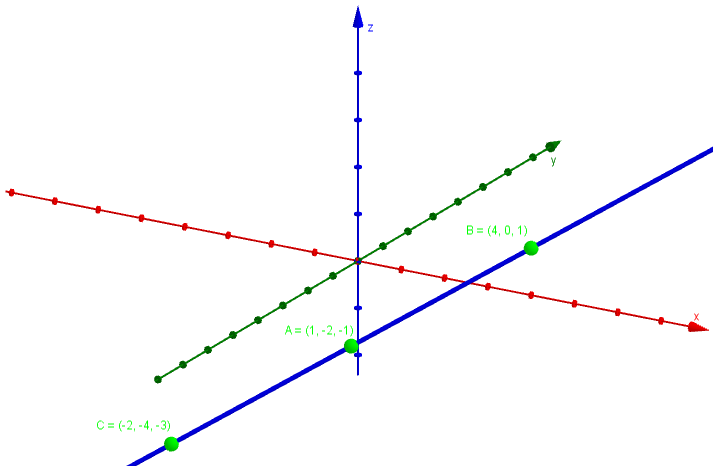
Bước 1 Định nghĩa ma trận $MatA$
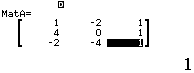
Bước 2 Định nghĩa ma trận $MatB$
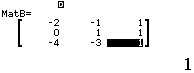
Bước 3 Tính định thức của ma trận $MatA$

Bước 4 Tính định thức của ma trận $MatB$
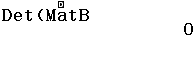
Vậy ba điểm đã cho thẳng hàng
3 Bốn điểm đồng phẳng trong không gian
Trong không gian $Oxyz$ cho bốn điểm $A=(x_a; y_a; z_a)$, $B=(x_b; y_b; z_b)$, $C=(x_c; y_c; z_c)$, $D=(x_d, y_d, z_d)$
$A, B, C, D$ đồng phẳng khi và chỉ khi $\left|\begin{array}{lll}x_{b}-x_{a}&y_{b}-y_{a}&z_{b}-z_{a}\\x_{c}-x_{a}&y_{c}-y_{a}&z_{c}-z_{a}\\x_{d}-x_{a}&y_{d}-y_{a}&z_{d}-z_{a}\end{array}\right|=0$
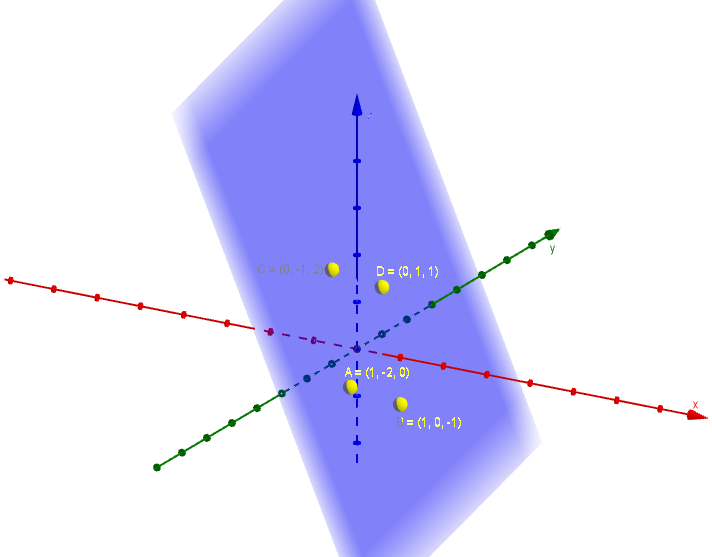
Trong không gian $Oxyz$ cho bốn điểm $A=(1; -2; 0)$, $B=(1; 0; -1)$, $C=(0; -1; 2)$, $D=(0; 1; 1)$
Chứng minh $A, B, C, D$ đồng phẳng
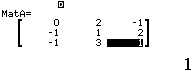
Bước 1 Định nghĩa ma trận $MatA$
Bước 2 Tính định thức của ma trận $MatA$

Vậy bốn điểm đã cho đồng phẳng