Xin chào tất cả các bạn.
Máy tính cầm tay CASIO có thể giải được mọi phương trình bậc ba nhưng không phải bao giờ nghiệm thu được cũng hiển thị được dưới dạng căn thức, một số phương trình khi giải nghiệm sẽ hiển thị dưới dạng thập phân.
Lúc bấy giờ bằng cách này hay cách khác chúng ta cần chuyển chúng sang dạng căn thức.
Ở đây, do chúng ta sử dụng tính năng Equation (Polynomial) nên sẽ dựa vào định lí Vi ét đảo.
Khi nào nghiệm tìm được bằng tính năng giải phương trình Solver mới sử dụng môi trường bảng giá trị Table hoặc môi trường bảng tính Spreadsheet.
#1. Các bước xử lí
Bước 1. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc ba
Bước 2. Lần lượt gán hai nghiệm đang hiển thị dưới dạng thập phân vào biến nhớ A và B
Bước 3.
- Nếu hai nghiệm vừa gán là nghiệm thực thì chọn môi trường thông thường Calculate
- Nếu hai nghiệm vừa gán là nghiệm phức thì chọn môi trường số phức Complex
Bước 4. Tính A+B và AB
Giả sử A+B=S và AB=P
Chú ý. Nếu S và P hiển thị dưới dạng thập phân hữu hạn hoặc thập phân vô hạn tuần hoàn thì bạn cần chuyển sang phân số
Bước 5. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc hai một ẩn $x^2-Sx+P=0$
#2. Thực hành xử lí trên 880 BTG
Ví dụ 1. Giải phương trình $25x^3-70x^2+41x-2=0$
Bước 1. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc ba $25x^3-70x^2+41x-2=0$
Bước 1.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomaial => nhấn phím OK => chọn $ax^3+bx^2+cx+d$ => nhấn phím OK


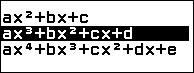
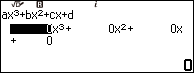
Bước 1.2. Nhập 25 => nhấn phím EXE => nhập -70 => nhấn phím EXE => nhập 41 => nhấn phím EXE => nhập -2 => nhấn phím EXE
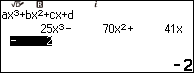
Bước 1.3. Nhấn phím EXE => nhấn phím EXE => nhấn phím EXE
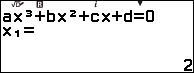
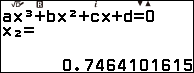
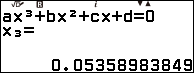
Bước 2. Lần lượt gán hai nghiệm $x_2$ và $x_3$ vào biến nhớ A và B
Bước 2.1. Nhấn phím VARIABLE => chọn biến nhớ A => nhấn phím EXE => chọn Store => nhấn phím EXE
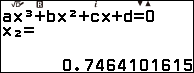
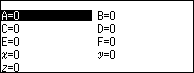

Bước 2.2. Nhấn phím VARIABLE => chọn biến nhớ => nhấn phím EXE => chọn Store => nhấn phím EXE
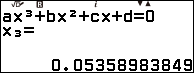
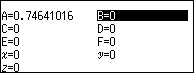

Bước 3. Vì hai nghiệm $x_2$ và $x_3$ là nghiệm thực nên chọn môi trường thông thường Calculate
Nhấn phím HOME => chọn Calculate => nhấn phím OK


Bước 4. Tính A+B và AB
Bước 4.1. Nhập A+B => nhấn phím EXE

Bước 4.2. Nhập AB => nhấn phím EXE

Bước 5. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc hai một ẩn $x^2-\frac{4}{5}x+\frac{1}{25}=0$
Bước 5.1. Nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomaial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK


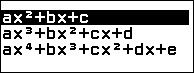
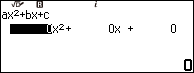
Bước 5.2. Nhập 1 => nhấn phím EXE => nhập $-\frac{4}{5}$ => nhấn phím EXE => nhập $\frac{1}{25}$ => nhấn phím EXE

Bước 5.3. Nhấn phím EXE => nhấn phím EXE
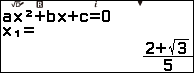
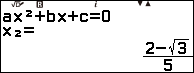
Vậy phương trình bậc ba đã cho có ba nghiệm là 2, $\frac{2+\sqrt{3}}{5}$ và $\frac{2-\sqrt{3}}{5}$
Ví dụ 2. Giải phương trình $7x^3-27x^2+20x-6=0$
Thực hiện tương tự Bước 1 của Ví dụ 1 chúng ta thu được ba nghiệm
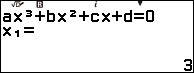


Thực hiện tương tự Bước 2 của Ví dụ 1 chúng ta gán được $x_2$ và $x_3$ vào biến nhớ A và B
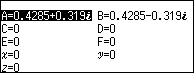
Vì hai nghiệm $x_2$ và $x_3$ là nghiệm phức nên chọn môi trường số phức Complex
Nhấn phím HOME => chọn Complex => nhấn phím OK

Thực hiện tương tự Bước 4 và Bước 5 của Ví dụ 1 chúng ta thu được



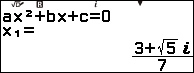
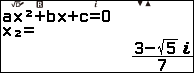
Vậy phương trình bậc ba đã cho có ba nghiệm là 3, $\frac{3+\sqrt{5}i}{7}$ và $\frac{3-\sqrt{5}i}{7}$
#3. Thực hành xử lí trên 580 VN X
Ví dụ 1. Giải phương trình $25x^3-70x^2+41x-2=0$
Bước 1. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc ba $25x^3-70x^2+41x-2=0$
Bước 1.1. Nhấn phím MENU => chọn Equation => nhấn phím = => nhấn phím 2 => nhấn phím 3
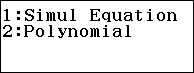
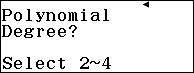
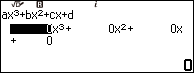
Bước 1.2. Nhập 25 => nhấn phím = => nhập -70 => nhấn phím = => nhập 41 => nhấn phím = => nhập -2 => nhấn phím =
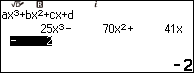
Bước 1.3. Nhấn phím = => nhấn phím = => nhấn phím =
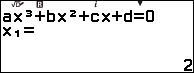
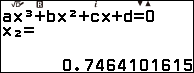
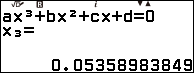
Bước 2. Lần lượt gán hai nghiệm $x_2$ và $x_3$ vào biến nhớ A và biến nhớ B
Bước 2.1. Nhấn phím STO => nhấn phím (-)
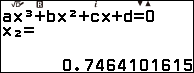

Bước 2.2. Nhấn phím STO => nhấn phím ![]()
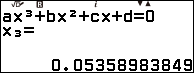

Bước 3. Vì hai nghiệm $x_2$ và $x_3$ là nghiệm thực nên chọn môi trường thông thường Calculate
Nhấn phím MENU => chọn Calculate => nhấn phím =

Bước 4. Tính A+B và AB
Bước 4.1. Nhập A+B => nhấn phím =

Bước 4.2. Nhập AB => nhấn phím = => nhập 0.04 => nhấn phím =


Bước 5. Sử dụng tính năng Equation (Polynomial) giải phương trình bậc hai một ẩn $x^2-\frac{4}{5}x+\frac{1}{25}=0$
Bước 5.1. Nhấn phím MENU => chọn Equation => nhấn phím = => nhấn phím 2 => nhấn phím 2
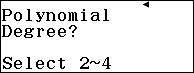
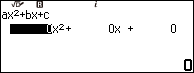
Bước 5.2. Nhập 1 => nhấn phím = => nhập $-\frac{4}{5}$ => nhấn phím = => nhập $\frac{1}{25}$ => nhấn phím =

Bước 5.3. Nhấn phím = => nhấn phím =
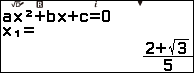
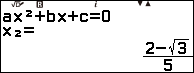
Vậy phương trình bậc ba đã cho có ba nghiệm là 2, $\frac{2+\sqrt{3}}{5}$ và $\frac{2-\sqrt{3}}{5}$
Ví dụ 2. Giải phương trình $7x^3-27x^2+20x-6=0$
Thực hiện tương tự Bước 1 của Ví dụ 1 chúng ta thu được ba nghiệm
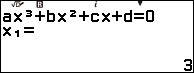


Thực hiện tương tự Bước 2 của Ví dụ 1 chúng ta gán được $x_2$ và $x_3$ vào biến nhớ A và biến nhớ B

Vì hai nghiệm $x_2$ và $x_3$ là nghiệm phức nên chọn môi trường số phức Complex
Nhấn phím MENU=> chọn Complex => nhấn phím =
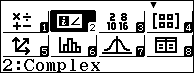

Thực hiện tương tự Bước 4 và Bước 5 của Ví dụ 1 chúng ta thu được



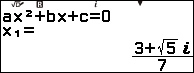
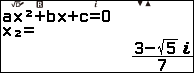
Vậy phương trình bậc ba đã cho có ba nghiệm là 3, $\frac{3+\sqrt{5}i}{7}$ và $\frac{3-\sqrt{5}i}{7}$
#4. Lời kết
Trên đây là chi tiết các bước xử lí nghiệm xấu khi giải phương trình bậc ba bằng máy tính cầm tay CASIO.
Thủ thuật này sẽ giúp bạn giải quyết được hầu hết các phương trình bậc ba, trong một số ít trường hợp không giải quyết được thì cách duy nhất là bạn giải bằng phương pháp Toán học (phương pháp Cardano).
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.





1 Comment