Xin chào tất cả các bạn
Hàm số phân thức hữu tỉ là một những hàm số thường gặp trong chương trình Toán học Trung học Phổ thông
Mặc dù việc xác định cực trị của hàm số này tương tự như các hàm đa thức nhưng thao tác lấy đạo hàm và giải phương trình đạo hàm khá tốn thời gian
Biết được khó khăn trên, hôm nay, mình sẽ hướng dẫn các bạn xác định nhanh các điểm cực trị của hàm phân thức hữu tỉ bằng máy tính cầm tay CASIO fx 880 BTG
Xem thêm
1 Sơ lược về cực trị của hàm phân thức
Trong phạm vi ngắn gọn của bài viết này chúng ta chỉ xác định điểm cực trị của hàm phân thức hữu tỉ tam thức trên nhị thức $y=\frac{ax^2+bx+c}{a’x+b’}$ với $a \neq 0, a’ \neq 0$
- Hàm số y nếu có cực trị thì sẽ có hai cực trị
- Hai điểm cực trị này đối xứng với nhau qua tâm đối xứng của đồ thị
- Tâm đối xứng của đồ thị là giao điểm của hai đường tiệm cận
Suy ra, chỉ cần xác định được hoành độ của một điểm cực trị xem xác định được tọa độ của các điểm cực trị
2 Sơ lược về phép đối xứng tâm
Trong hệ tọa độ $Oxy$ cho điểm $I(a, b)$. Nếu phép đối xứng tâm $D_I$ biến điểm $M(x, y)$ thành điểm $M’(x’, y’)$ thì $\left\{\begin{array}{l}x’=2a-x\\y’=2b-y\end{array}\right.$
3 Các bước xác định
Chẳng hạn mình cần xác định các điểm cực trị của hàm số $y=\frac{ax^2+bx+c}{a’x+b’}$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 sử dụng tính năng Function gán hàm số đã cho vào hàm nhớ f(x)
Bước 2 sử dụng tính năng Solver và tính năng Derivative với giá trị x ban đầu bất kì dò tìm nghiệm của phương trình $y’=0$
Giả sử tìm được nghiệm $x_1$
Bước 3 tiếp tục sử dụng tính năng Solver và tính năng Derivative với giá trị x ban đầu là $2 \times (-\frac{b’}{a’}) – x_1$ dò tìm nghiệm của phương trình $y’=0$
Giả sử tìm được nghiệm là $x_2$
Bước 4 sử dụng tính năng Function xác định trung độ của các điểm cực trị
4 Thực hành xác định
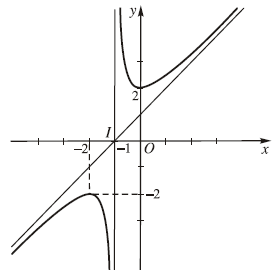
Chẳng hạn mình cần xác định các điểm cực trị của hàm số $y=\frac{x^2+2x+2}{x+1}$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 sử dụng tính năng Function gán hàm số đã cho vào hàm nhớ f(x)
Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK => nhập $\frac{x^2+2x+2}{x+1}$ => nhấn phím EXE
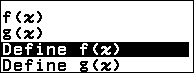
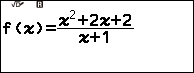
Bước 2 sử dụng tính năng Solver và tính năng Derivative với giá trị x ban đầu bất kì dò tìm nghiệm của phương trình $y’=0$
Bước 2.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Solver => nhấn phím OK



Bước 2.2 nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

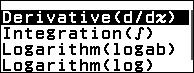
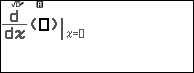
Bước 2.3 nhấn phím FUNCTION => chọn f(x) => nhấn phím OK
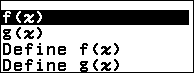
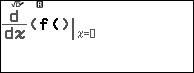
Bước 2.4 nhấn phím x => nhấn phím ) => nhấn phím SHIFT => nhấn phím ![]() => nhấn phím x
=> nhấn phím x
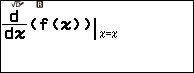
Bước 2.5 nhấn phím EXE => nhấn phím ![]() => nhấn phím EXE
=> nhấn phím EXE


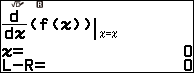
Suy ra hoành độ của điểm cực trị thứ nhất là 0
Bước 3 tiếp tục sử dụng tính năng Solver và tính năng Derivative với giá trị x ban đầu là $2 \times (-1) – 0$ dò tìm nghiệm của phương trình $y’=0$
Nhấn phím EXE => nhấn phím EXE => nhập $2 \times (-1) – 0$ => nhấn phím EXE => nhấn phím EXE


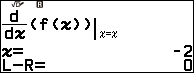
Suy ra hoành độ của điểm cực trị thứ nhì là -2
Bước 4 sử dụng tính năng Function xác định trung độ của các điểm cực trị
Bước 4.1 nhấn phím HOME => chọn Calculate => nhấn phím OK


Bước 4.2 nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập 0 => nhấn phím EXE
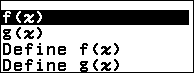

Suy ra trung độ của điểm cực trị thứ nhất là 2
Bước 4.3 nhấn phím FUNCTION => chọn f(x) => nhấn phím OK => nhập -2 => nhấn phím EXE
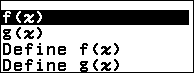

Suy ra trung độ của điểm cực trị thứ nhì là -2
Vậy tọa độ các điểm cực trị của hàm số đã cho là (0, 2) và (-2, -2)
https://youtu.be/Y5CReYbfQCg
5 Lời kết
Trên đây là chi tiết các bước xác định tọa độ của các điểm cực trị của hàm phân thức hữu tỉ bằng máy tính cầm tay CASIO fx 880 BTG
Trường hợp khi nghiệm của phương trình y’=0 là một số thập phân thì bạn hãy gán nó vào biến nhớ
Trường hợp máy tính cầm tay thông báo Cannot Solve thì hàm số đã cho không có cực trị
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo