Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn cách viết phương trình đường tròn đi qua ba điểm không thẳng hàng bằng máy tính cầm tay CASIO fx 880 BTG

1 Kiến thức Toán học
Giả sử phương trình đường tròn cần tìm có dạng $x^2+y^2-2ax-2by+c=0$ và tọa độ của ba điểm đi qua là $(x_1, y_1), (x_2, y_2), (x_3, y_3)$
Lúc bấy giờ $a, b, c$ là nghiệm của hệ ba phương trình bậc nhất ba ẩn $\left\{\begin{array}{l}x_1^2+y_1^2-2ax_1-2by_1+c=0\\x_2^2+y_2^2-2ax_2-2by_2+c=0\\x_3^2+y_3^2-2ax_3-2by_3+c=0\end{array}\right. \Leftrightarrow \left\{\begin{array}{l}2x_1a+2y_1b-c=x_1^2+y_1^2\\2x_2a+2y_2b-c=x_2^2+y_2^2\\2x_3a+2y_3b-c=x_3^2+y_3^2\end{array}\right.$
Tìm được $a, b, c$ sẽ viết được phương trình đường tròn
Bao giờ chúng ta cũng viết được một và chỉ một phương trình đường tròn đi qua ba điểm không thẳng hàng
2 Các bước thực hiện
Bước 1 giải hệ ba phương trình bậc nhất ba ẩn $\left\{\begin{array}{l}2x_1a+2y_1b-c=x_1^2+y_1^2\\2x_2a+2y_2b-c=x_2^2+y_2^2\\2x_3a+2y_3b-c=x_3^2+y_3^2\end{array}\right.$
Mẹo nhớ nhanh các hệ số của hệ ba phương trình bậc nhất ba ẩn là “hai lần hoành độ” “hai lần trung độ” -1 “tổng của bình phương hoàng độ và trung độ”
Bước 2 viết phương trình đường tròn
3 Ví dụ minh họa
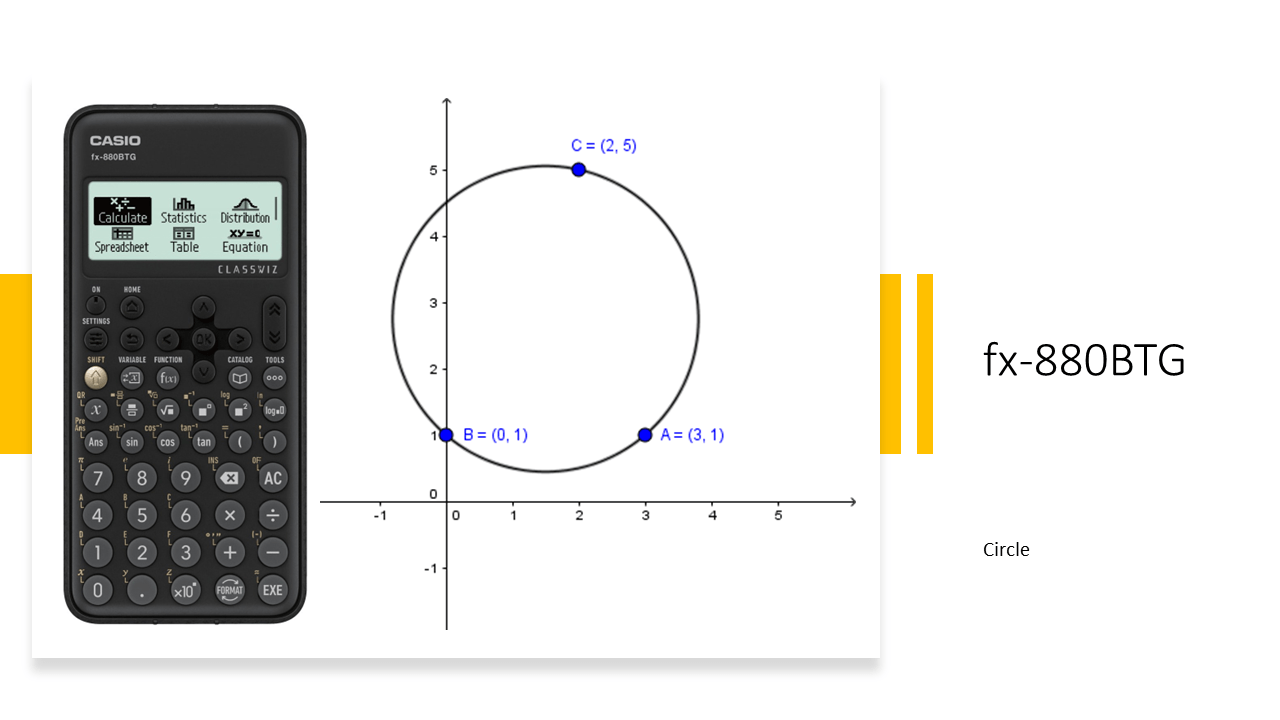
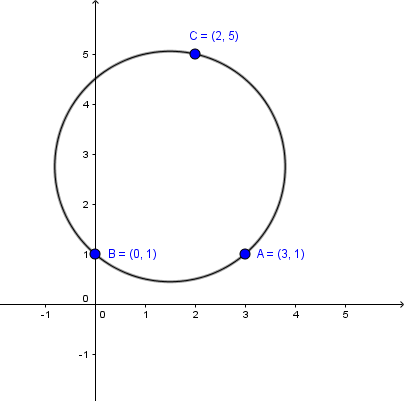
Chẳng hạn mình cần viết phương trình đường tròn đi qua ba điểm $A=(3, 1)$ và $B=(0, 1)$ và $C=(2, 5)$ thì thực hiện tuần tự theo các bước bên dưới
Chỉ cần tìm được nghiệm của hệ ba phương trình $\left\{\begin{array}{llll}6x&+2y&-z&=10\\&2y&-z&=1\\4x&+10y&-z&=29\end{array}\right.$ là sẽ viết được phương trình đường tròn
Bước 1 nhấn phím HOME => sử dụng các phím ![]() con trỏ chọn Equation => nhấn phím OK
con trỏ chọn Equation => nhấn phím OK

Bước 2 chọn Simul Equation => nhấn phím OK

Bước 3 chọn 3 Unknowns => nhấn phím OK

Bước 4 nhập các hệ số của hệ ba phương trình
- Nhập 6 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập -1 => nhấn phím EXE => nhập 10 => nhấn phím EXE
- Nhập 0 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập -1 => nhấn phím EXE => nhập 1 => nhấn phím EXE
- Nhập 4 => nhấn phím EXE => nhập 10 => nhấn phím EXE => nhập -1 => nhấn phím EXE => nhập 29 => nhấn phím EXE
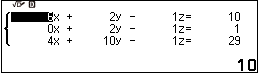
Bước 5 nhấn phím EXE để giải hệ ba phương trình



Suy ra hệ ba phương trình có một nghiệm là $\left(\frac{3}{2}, \frac{11}{4}, \frac{9}{2}\right)$
Suy $a=\frac{3}{2}$ và $b=\frac{11}{4}$ và $c=\frac{9}{2}$
Vậy phương trình đường tròn đi qua ba điểm đã cho là $x^2+y^2-3x-\frac{11}{2}y+\frac{9}{2}=0$
Xem thêm Cách giải hệ ba phương trình bậc nhất ba ẩn bằng CASIO fx 880 BTG
https://youtube.com/shorts/jlNgGeaU1Rk?feature=share
4 Lời kết
Viết phương trình đường tròn đi qua ba điểm không thẳng hàng bằng máy tính cầm tay CASIO fx 880 BTG là một trong thủ thuật kinh điển, thường được sử dụng trong học tập, kiểm tra và thi cử
Ngoài ra thủ thuật này còn được sử dụng để tìm giao điểm (hoành độ, trung độ) của ba đường trung trực của tam giác khi biết tọa độ ba đỉnh của tam giác
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo