Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn cho các bạn chi tiết các bước tìm ma trận đơn vị và ma trận chuyển vị bằng máy tính cầm tay CASIO fx 580 VN X
Trong thực tế chúng ta hầu như không bao giờ có nhu cầu tìm ma trận đơn vị, chuyển vị bằng CASIO fx 580 VN X (quá dễ) ngoại trừ một số trường hợp đặc biệt
1 Sơ lược về ma trận đơn vị và ma trận chuyển vị
Chỉ có ma trận vuông mới có ma trận đơn vị, ma trận đơn vị thường được ký hiệu là $I_n$ với n là một số nguyên dương
Mọi ma trận đều có ma trận chuyển vị, nếu ma trận là ma trận vuông thì ma trận sau khi chuyển vị cũng là ma trận vuông
Xem thêm Tính định thức của ma trận
2 Ma trận đơn vị
Chẳng hạn mình cần tìm ma trận đơn vị của ma trận vuông cấp $4 \times 4$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 mở phương thức ma trận
Nhấn phím MENU => nhấn phím 4 để chọn Matrix
Bước 2 gọi lệnh Identity
Nhấn phím OPTN => nhấn phím 
=> nhấn phím 4 để chọn lệnh Identity
Bước 3 nhập cấp của ma trận
Ở đây mình sẽ nhập 4
Bước 4 nhấn phím =
Vậy ma trận đơn vị của ma trận vuông cấp $4 \times 4$ là $\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}\right]$
3 Ma trận chuyển vị
Chẳng hạn mình cần tìm ma trận chuyển vị của ma trận $\left[\begin{matrix}2&1&1\\8&1&8\end{matrix}\right]$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 mở phương thức ma trận Matrix
Nhấn phím MENU => nhấn phím 4 để chọn Matrix
Bước 2 gán ma trận vào biến nhớ ma trận MatA
Bước 2.1 nhấn phím 1 để chọn MatA
Bước 2.2 nhấn phím 2 để khai báo ma trận đang gán có 2 dòng
Bước 2.3 nhấn phím 3 để khai báo ma trận đang gán có 3 cột
Bước 2.4 lần lượt nhấn các phím 
để nhập các phần tử của ma trận
Bước 3 nhấn phím AC
Bước 4 gọi lệnh Transposition
Nhấn phím OPTN => nhấn phím => nhấn phím 3 để chọn Transposition
Bước 5 gọi ma trận MatA
Nhấn phím OPTN => nhấn phím 3 để chọn MatA
Bước 6 nhấn phím =
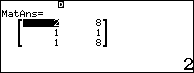
Vậy ma trận chuyển vị của ma trận đã cho là $\left[ \begin{matrix}2&8\\1&1\\1&8\end{matrix}\right]$
4 Lời kết
Qua bài viết này chúng ta đã cùng nhau tìm hiểu xong cách tìm ma trận đơn vị và ma trận chuyển vị bằng máy tính cầm tay CASIO fx 580 VN X
Nếu không có gì thay đổi, đến đây mình cũng xin khép lại mách kiến thức về ma trận trên CASIO fx 580 VN X
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
