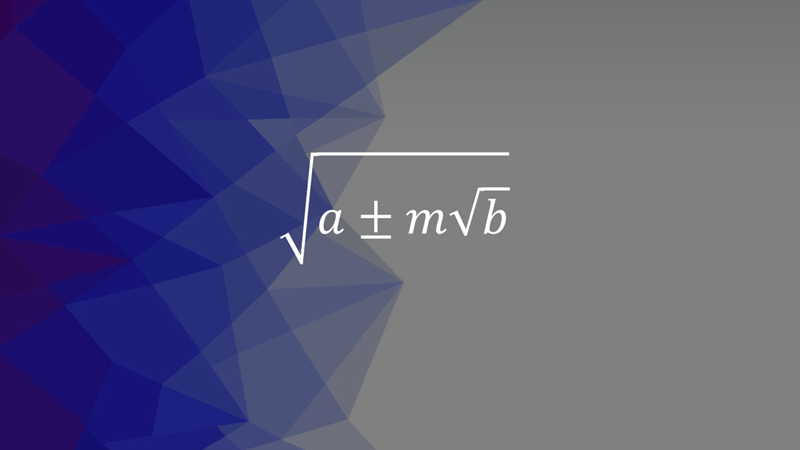Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước rút gọn biểu thức chứa căn thức bậc hai có dạng $\sqrt{a \pm m\sqrt{b}}$ bằng máy tính cầm tay CASIO fx 880 BTG
Trong một số trường hợp chúng có thể rút gọn trực tiếp nhưng nếu chỉ viết kết quả thì chắc chắn không được điểm cao
Mặc khác, biểu thức chứa căn thức bậc hai này là một trong những dạng thường gặp trong chương trình Toán 9 và trong Kì thi tuyển sinh vào lớp 10
Xem thêm Giải phương trình bậc hai
1 Các bước rút gọn biểu thức
Giả sử mình cần rút gọn biểu thức chứa căn thức bậc hai có dạng $\sqrt{a \pm m\sqrt{b}}$ thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Bước 1 sử dụng tính năng Equation giải phương trình bậc hai $x^2-ax+\frac{m^2b}{4}=0$
Bước 2
Giả sử tìm được hai nghiệm là $x_1$ và $x_2$
Lúc bấy giờ, chúng ta chỉ việc áp dụng công thức $\sqrt{a \pm m\sqrt{b}}$ $=$ $\sqrt{(\sqrt{x_1} \pm \sqrt{x_2})^2}$ $=$ $|\sqrt{x_1}+\sqrt{x_2}|$

2 Thực hành rút gọn biểu thức
Giả sử mình cần rút gọn biểu thức chứa căn thức bậc hai $\sqrt{12 + 2\sqrt{35}}$ thì thực hiện tuần tự theo các chỉ dẫn bên dưới
Bước 1 giải phương trình bậc hai $x^2-12x+\frac{2^2 \times 35}{4}=0$
Bước 1.1 nhấn phím HOME => chọn Equation => nhấn phím OK => chọn Polynomial => nhấn phím OK => chọn $ax^2+bx+c$ => nhấn phím OK



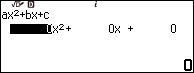
Bước 1.2 nhập 1 => nhấn phím EXE => nhập -12 => nhấn phím EXE => nhập 35 => nhấn phím EXE
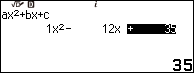
Bước 1.3 nhấn phím EXE => nhấn phím EXE
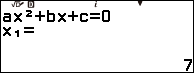

Bước 2
Suy ra phương trình $x^2-12x+\frac{2^2 \times 35}{4}=0$ có hai nghiệm thực phân biệt là $x_1=7$ và $x_2=5$
Vậy $\sqrt{12+2\sqrt{35}}=\sqrt{(\sqrt{7}+\sqrt{5})^2}=|\sqrt{7}+\sqrt{5}|=\sqrt{7}+\sqrt{5}$
3 Trình bày lời giải
Trong kiểm tra hoặc thi cử, khi tìm được $x_1=7$ và $x_2=5$ chúng ta nên trình bày như sau
$\sqrt{12+2\sqrt{35}}$
$=\sqrt{(\sqrt{7})^2+(\sqrt{5})^2+2\sqrt{7}\sqrt{5}}$
$=\sqrt{(\sqrt{7}+\sqrt{5})^2}$
$=|\sqrt{7}+\sqrt{5}|$
$=\sqrt{7}+\sqrt{5}$
https://youtube.com/shorts/SJ8RpeUh-EY?feature=share
4 Lời kết
Hy vọng thủ thuật rút gọn biểu thức chứa căn thức bậc hai có dạng $\sqrt{a \pm m\sqrt{b}}$ bằng máy tính cầm tay CASIO fx 880 BTG sẽ hữu ích
Mình luôn khuyến khích các bạn sử dụng kiến thức Toán học nhưng nếu kiến thức Toán học có hạn hoặc thời gian không cho phép thì các bạn cứ sử dụng thủ thuật máy tính cầm tay
Mặc khác, việc sử dụng thủ thuật máy tính cần tay mà tìm được kết quả đúng vẫn tốt hơn không tìm được kết quả hoặc tìm được kết quả sai
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo