Xin chào tất cả các bạn
Hôm nay, mình sẽ hướng dẫn các bạn chi tiết các bước giải phương trình bậc nhất đối với hàm số lượng giác sin x và cos x bằng máy tính cầm tay CASIO fx 880 BTG
Xem thêm Pol – Chuyển tọa độ chữ nhật sang tọa độ cực
1 Sơ lược về phương trình a sin x + b cos x = c
Phương trình có dạng a sin x + b cos x = c với a, b, c là những số đã cho và a khác 0 hoặc b khác 0 được gọi là phương trình bậc nhất đối với hàm số lượng giác sin x và cos x
Thông thường, để giải phương trình lượng giác này chúng ta sẽ cố gắng biến đổi vế trái thành biểu thức $r\sin(x+\theta)$
Lúc bấy giờ phương trình lượng giác đã cho sẽ tương đương với $r\sin(x+\theta)=c$
Dưới đây là chi tiết các bước tìm r và $\theta$ bằng máy tính cầm tay CASIO fx 880 BTG
2 Các bước giải phương trình
Chẳng hạn mình cần giải phương trình a sin x + b cos x = c thì thực hiện tuần tự theo các bước bên dưới
Bước 1 cài đặt đơn vị góc là rađian
Bước 2 sử dụng tính năng Rect to Polar tìm r và $\theta$
Bước 3 lúc bấy giờ phương trình đã cho tương đương với $\sin(x+\theta)=\frac{c}{r}$
3 Thực hành giải phương trình
Chẳng hạn mình cần giải phương trình $\sqrt{3}\sin x-\cos x=1$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 cài đặt đơn vị góc là rađian
Nhấn phím SETTINGS => chọn Calc Settings => nhấn phím OK => chọn Angle Unit => nhấn phím OK => chọn Radian => nhấn phím OK => nhấn phím AC



Bước 2 sử dụng tính năng Rect to Polar tìm r và $\theta$
Bước 2.1 nhấn phím CATALOG => chọn Angle / Coord / Sexa => nhấn phím OK => chọn Rect to Polar => nhấn phím OK



Bước 2.2 nhập $\sqrt{3}$ => nhấn phím SHIFT => nhấn phím ) => nhập -1 => nhấn phím EXE



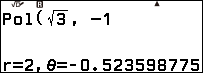
Bước 2.3 nhấn phím VARIABLE => chọn biến nhớ y => nhấn phím OK => chọn Recall => nhấn phím OK => nhấn phím OK
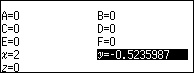



Suy ra r = 2 và $\theta=-\frac{\pi}{6}$
Bước 3 lúc bấy giờ phương trình đã cho tương đương với $\sin \left(x-\frac{\pi}{6}\right)=\frac{1}{2}$
Bước 3.1 nhấn phím SHIFT => nhấn phím sin => nhập $\left.\frac{1}{2}\right)+\frac{\pi}{6}$ => nhấn phím EXE

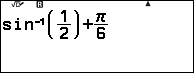
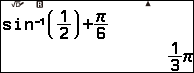
Bước 3.2 nhập $\pi-\sin^{-1}\left(\frac{1}{2}\right)+\frac{\pi}{6}$ => nhấn phím EXE
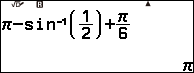
Vậy phương trình đã cho có nghiệm là $x=\frac{\pi}{3}+k 2 \pi$ và $x=\pi+k 2 \pi$
https://youtu.be/TeRWRXR5czM
4 Lời kết
Trên đây là chi tiết các bước giải phương trình bậc nhất đối với hàm số lượng giác sin x và cos x bằng máy tính cầm tay CASIO fx 880 BTG
Trong thực hành khi gặp trường hợp không tìm được chính xác r và $\theta$ (có giá trị xấu) thì hãy sử dụng arcsin các bạn nhá
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo