Xin chào tất cả các bạn.
Như các bạn đã biết, mặc dù tính năng giải phương trình Solver cho phép chúng ta giải phương trình bất kì (đa thức, phân thức, căn thức, …)
Ưu điểm là vậy nhưng tính năng này cũng có không ích nhược điểm, một trong những nhược điểm lớn nhất là không hiển thị được nghiệm dưới dạng căn thức.
Hôm nay, mình sẽ chia sẽ với các bạn một phương pháp mới (sử dụng môi trường bảng tính Spreadsheet của máy tính 880 BTG) cho phép chuyển nghiệm thập phân vô hạn không tuần hoàn sang nghiệm căn thức.
#1. Sơ lược về thủ thuật chuyển nghiệm
Thủ thuật này sẽ cho phép chúng ta chuyển một nghiệm thập phân vô hạn không tuần hoàn sang nghiệm căn thức.
Nghiệm căn thức có thể là một trong các dạng $\sqrt{a}, \frac{\sqrt{a}}{b}, a+\sqrt{b}, \frac{a+\sqrt{b}}{c}$ với a, b, c là những số nguyên dương.
Các nghiệm này thường gặp khi giải phương trình có chứa căn thức (phương trình vô tỉ) bằng tính năng giải phương trình Solver.
#2. Các bước chuyển nghiệm
Bước 1. Sử dụng tính năng giải phương trình Solver
Bước 2. Mở môi trường bảng tính Spreadsheet
Bước 2.1. Nhập 1 vào ô A1
Bước 2.2. Sử dụng tính năng Fill Formula nhập các giá trị -22, -21, -20, … , 20, 21, 22 vào cột B
Bước 2.3. Sử dụng tính năng Fill Formula với Form $A \textdollar 1x^2+B1x$ và Range B1:B45
Bước 2.4. Quan sát bảng tính Spreadsheet cố gắng xác định một giá trị nguyên ở cột C
Giả sử giá trị nguyên là $\beta$, lúc bấy nghiệm của phương trình đã cho $1x^2+\alpha x-\beta=0$
- 1 là giá trị được nhập ở Bước 2.1
- $\alpha$ là giá trị ở cột B (so với giá trị nguyên $\beta$) ở cột C
Chú ý: Trong trường hợp không may khi nhập 1 ở Bước 2.1 mà không tìm được giá trị nguyên $\beta$ thì thử với 2, 3, 4, …
Lúc bấy giờ phương trình bậc hai một ẩn cần tìm sẽ là $2$ hoặc $3$ hoặc $4$ hoặc $…$ $x^2+\alpha x-\beta=0$
Bước 3. Sử dụng tính năng giải phương trình đa thức Equation (Polynomial) giải phương trình bậc hai vừa xác định được
#3. Thực hành chuyển nghiệm
Giải phương trình $\sqrt{2x+3}=2x-5$
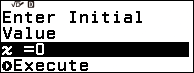
Bước 1. Sử dụng tính năng giải phương trình Solver
Bước 1.1. Nhấn phím HOME => chọn Equation => nhấn phím EXE => chọn Solver => nhấn phím EXE



Bước 1.2. Nhập $\sqrt{2x+3}=2x-5$ => nhấn phím EXE => nhấn phím ![]() => nhấn phím EXE
=> nhấn phím EXE
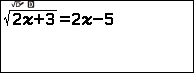

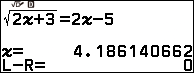
Bước 2. Mở môi trường bảng tính Spreadsheet
Nhấn phím HOME => chọn Spreadsheet => nhấn phím EXE

Bước 2.1. Chọn ô A1 => nhập 1 => nhấn phím EXE
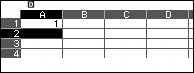
Bước 2.2.
Chọn ô B1 => nhập -22 => nhấn phím EXE
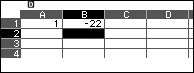
Nhấn phím TOOLS => chọn Fill Formula => nhấn phím EXE => nhập B1+1 => nhấn phím EXE => nhập B2:B45 => nhấn phím EXE => nhấn phím EXE
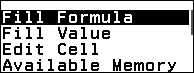
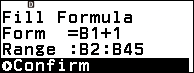
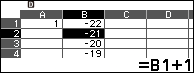
Gợi ý: Nhấn phím CATALOG => chọn Spreadsheet => nhấn phím EXE => chọn : => nhấn phím EXE để nhập :
Bước 2.3.
Chọn ô C1 => nhấn phím TOOLS => chọn Fill Formula => nhấn phím EXE => nhập $A \textdollar 1x^2+B1x$ => nhấn phím EXE => nhập B1:B45 => nhấn phím EXE => nhấn phím EXE



Bước 2.4.
Với A1 = 1 không tồn tại giá trị nguyên $\beta$
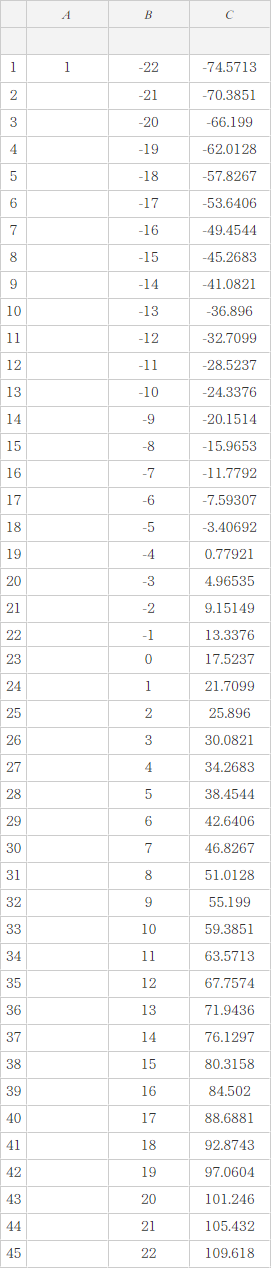
Với A1 = 2 tồn tại giá trị nguyên $\beta=-11$ và giá trị nguyên $\alpha=-11$

Lúc bấy giờ phương trình bậc hai một ẩn cần tìm sẽ là $2x^2-11x+11=0$
Bước 3. Sử dụng tính năng giải phương trình đa thức Equation (Polynomial) giải phương trình bậc hai vừa xác định được
Nhấn phím HOME => chọn Equation => nhấn phím EXE => chọn Polynomial => nhấn phím EXE => chọn $ax^2+bx+c$ => nhấn phím EXE


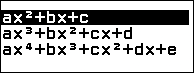
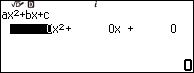
Nhập 2 => nhấn phím EXE => nhập -11 => nhấn phím EXE => nhập 11 => nhấn phím EXE
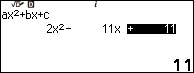
Nhấn phím EXE
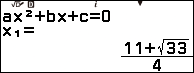
Vậy nghiệm của phương trình vô tỉ đã cho là $\frac{11+\sqrt{33}}{4}$
#4. Lời kết
Mọi số thập phân vô hạn không tuần hoàn có dạng $\frac{a+\sqrt{b}}{c}$ đều là nghiệm của phương trình bậc hai một ẩn nào đó.
Tuy nhiên không phải bao giờ việc sử dụng môi trường bảng tính Spreadsheet của máy tính 880 BTG cũng chuyển được nghiệm thập phân sang nghiệm căn thức.
Nói cách khác là xác định được phương trình bậc hai một ẩn, các giá trị -22, -21, -20, …, 20, 21, 22 chỉ là những giá trị hy vọng.
Ngoài ra, nếu bạn sử dụng 580 VN X thì bạn có thể thực hiện thông qua môi trường bảng giá trị Table.
Gợi ý:
1 hoặc 2 hoặc 3 hoặc … hoặc $A^2+Ax$ với A là biến nhớ chứa nghiệm của phương trình đã cho.
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.




