Vì fx 880 BTG không có phím tính tổ hợp chập k của n phần tử như những phiên bản trước nên chúng ta không thể tính bằng cách nhấn trực tiếp vào phím nCr
Muốn tính được tổ hợp chập k của n phần tử chúng ta cần biết cách sử dụng tính năng Combination (C) trong CATALOG
Cách sử dụng tính năng Combination (C) không có gì phức tạp tuy nhiên ít nhiều gì cũng gây khó khăn cho người mới
Bài viết này ra đời không ngoài mục đích giúp các bạn mới sử dụng máy tính cầm tay CASIO fx 880 BTG có thể tính được số các tổ hợp chập k của n phần tử một cách dễ dàng
Sách giáo khoa thường kí hiệu tổ hợp chập k của n phần tử là $C_n^k$ còn fx 880 BTG là $nCk$
1 Nhắc lại một số kiến thức về tổ hợp
Cho tập hợp $A$ gồm $n$ phần tử $(n \geq 1)$
Mỗi tập hợp con gồm $k$ phần tử của $A$ được gọi là một tổ hợp chập $k$ của $n$ phần tử
Các nhà Toán học đã quy ước tổ hợp chập $0$ của $n$ phần tử là tập hợp rỗng
Số các tổ hợp chập $k$ của $n$ phần tử $(0 \leq k \leq n)$ được kí hiệu là $C_n^k$ và được tính theo công thức $\frac{n!}{k!(n-k)!}$
2 Các cách tính số các tổ hợp chập k của n phần tử
Giả sử chúng ta cần tính số các tổ hợp chập $11$ của $13$
2.1 Cách 1 tính bằng máy tính cầm tay CASIO fx 880 BTG
Bước 1 nhập $n$ phần tử vào máy tính
Ở đây $n=13$ nên mình sẽ nhấn lần lượt các phím 
để nhập $13$ vào máy tính
Bước 2 nhấn phím CATALOG => chọn Probability => nhấn phím OK => chọn Combination (C) => nhấn phím OK
Bước 3 nhập $k$ vào máy tính
Ở đây $k=11$ nên mình sẽ nhấn lần lượt các phím 
để nhập $11$ vào máy tính
Bước 4 nhấn phím EXE để xem số các tổ hợp chập $k$ của $n$ phần tử
Vậy số các tổ hợp chập $11$ của $13$ là $78$
2.2 Cách 2 tính trực tiếp thông công thức gốc
$C_{13}^{11}=\frac{13!}{11!(13-11)!}$
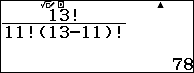
Vậy số các tổ hợp chập $11$ của $13$ là $78$
https://youtube.com/shorts/yw4MrBBR10k?feature=share
3 Lời kết
Tính năng Factorial (!), Permutation (P) và Combination (C) của máy tính cầm tay CASIO fx 880 BTG lần lượt cho phép chúng ta tính giai thừa (hoán vị), chỉnh hợp và tổ hợp
Bạn cần nhớ chính xác công dụng của từng tính năng để sử dụng cho đúng, đặc biệt là Permutation (P) và Combination (C)
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
